As my english is not very good, please if you see any mistake write me a private message about it.
In this task you are to count the number of different letters in the set. In my opinion the easiest way to do this looks like this. You just iterate over all small latin letters and check if the string contains it (with built-in functions).
443B - Kolya and Tandem Repeat
Let's add k question marks to the string. Than we can check all possible starting and ending positions of tandem repeat in a new string. We can check each of them in time O(n + k). We only need to check that some symbols are equal (in our task question mark is equal to every symbol).
It's obvious that the order of hints doesn't metter. There are 10 types of hints, so we can try all 210 vartiants of what other players should do. Now we need to check if Boris can describe all of his cards. He can do it iff he can distinguish all pairs of different cards. He can do it if somebody told at least one distinction. It can be a hint about color of one of cards (if they don't have same one) or it can be hint about value of some card.
Let's sort all friends in such a way that pi ≤ pj iff i ≤ j. If there is pi = 1 Andrey should ask only this friend. Now we can assume that all probabilities are less then 1. What should we maximize?
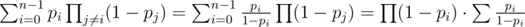
Let 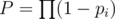 ,
, 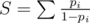 . Assume we already have some group of people we would ask a help. Let's look what will happen with the probability of success if we add a friend with probability pi to this group:
. Assume we already have some group of people we would ask a help. Let's look what will happen with the probability of success if we add a friend with probability pi to this group:
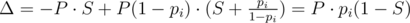
It means adding a new people to group will increase a probability of success only if S < 1. Now let's look at another question. We have some group of people with S < 1. And we want to add only one friend to this group. Which one is better? Let the probability of the first friend is pi and the second friend is pj. It's better to add first one if
Δi - Δj = P·pi·(1 - S) - P·pj·(1 - S) = P·(1 - S)·(pi - pj) > 0. As S < 1 we get pi > pj.
But it's only a local criteria of optimality. But, we can prove that globally you should use only a group of people with the biggest probabilities. We can use proof by contradiction. Let's look at the optimal answer with biggest used suffix (in the begining of editorial we sort all friends). Of all such answers we use one with minimum number of people in it. Where are two friends i and j (pi < pj) and i-th friend is in answer and j-th isn't. Let's look at the answer if we exclude i-th friend. It should be smaller because we used optimal answer with minimum numer of people in it. So adding a new people to this group will increase success probability. But we know that adding j-th is better than i-th. So we have found a better answer.
So we have a very easy solution of this problem. After sorting probabilities we should you some suffix of it. Because of sorting time complexity is O(nlogn).
It's obvious that we should never delete the first and last elements of array. Let's look at the minimum number. Let it be x and there are n elements in the array. We can subtract x from all elements and the answer for the problem will decrease on (n - 2)·x, becouse we will do n - 2 delitions of middle elements and each of this delitions will not give Artem exectly x more points.
If minimal element was the first or the last one, we can not to count it now (it equals to 0 now, so it will not affect the answer now). If it locates in the middle of array, we can prove that there is exist an optimal solution when Artem deletes this element on first move. We can prove it by contradaction. Let's look at the optimal answer where the minimal element is deleted on the minimal possible move (but not on first one). We can prove that we can delete it earlier. If move which is exactly before deleting minimum uses element of array which isn't a neighbour of minimual one we can swap this two delitions and it will not affect the answer. If those elements are neighbours we can write down the number of points which we obtain in both cases and understand that to delete minimum first is the best choice.
So, in this task we need to maintain a set of all not deleted elements and to find a smallest alive element. All of it we can do with built-in data structures in time O(nlogn).
First, let's solve the task with already built tree. We can do it with easy dymanic programming. We will count the answer for subtree with an edge to the parent. If we can count it for all vertices we can calculate the answer for the whole tree as maximum of answers for children of root. How to calculate it for one vertex? Suppose we already know answers for children of this vertex. We should color the edge to the parent in the same color as edge to the child with maximum answer. Let two maximum answers for child be max1 and max2 then the answer for this vertex would be max(max1, max2 + 1) if max1 ≥ max2.
What changes when we can add new vertices? Nothing. We can calculate the value of dynamic programming for new vertex (it always would be 1) and recalculate value for its parent. If it doesn't change we should stop this process, in another case we continue recalculations of dynamic programming values: go to its parent and recalculate answer for it and so on. If we maintain two maximums for each vertex in O(1) the asymptotic of the algorithm would be O(nlogn).
To prove it we can use some facts about Heavy-light decomposion. We can use the way Heavy-light decomposion splits edges of tree as our decomposition. We know that answer for such decomposition will be less than logarithm of the number of vertices. So each value of dynamic programming will be increased not more than O(logn) times.
442E - Gena and Second Distance
To solve this problem we can use a binary search. How do we check that answer if not less than R? It means that we can draw a circle with such radius which center locates in the rectangle and there are no more than one point inside this circle. How could we check it? We always can shift this circle in such a way that at least one point would be on its border. We can try all points as one which is on border. Than we should draw a circle with center in it and intersect it with n - 1 circles built on other points. If there is a point on this circle which is covered with no more than one other circle, than answer is greater or equal R. Finding such point is almost a typical problem which can be solved in O(klogk) where k — number of intersections points of circles.
We described a solution which works in O(logAnswer·n2·logn). But we can make it faster. Let's try all vertices as centers of circles and inside this loop make a binary search. We can make one optimize: if we can't find a point on circle with radius which is equal to the best now known than we shouldn't do a binary search in this point (because we can't increase the answer). It can be proved that this solution in avarage case works in O(logAnswer·nlog2n + n2logn) if we shuffle points. It's true because a binary search will be used in avarage only logn times. To prove this fact let's look at probability of binary search to be used in i-th step. If all values are different and shuffled it is  . It is known that sum of first n elements of this sirie is bounded by logn.
. It is known that sum of first n elements of this sirie is bounded by logn.
In this task there are some technical issues you need to know about. For example, we would do a binary search only O(logn) times if we find a stricly incresing subseqence of answers. That's why before using a binary search we should check that we can obtain not current answer but current answer plus some small value. Also we need to understand what "small value" is (it should be something like eps·curAnswer, where eps = 10 - 9, in another case you will probably have some problems with accuracy).
Also one interesting fact about this problem. If you write a solution with time compexity equal to O(logAnswer·n2·logn), it will work very fast on random tests becaue there are will be a very small number of circle intersections.











Amazing speed!!!!!How fast!!!! I think it is the fastest editorial....
where c, d , e editorial for div 2 ??
C,D,E Div2 are A,B,C div1
Can you put a code for them?
I like C problem very much. I also like D problem. Thank you for your interesting problems:D
I'm really impressed with the quality of the problems and the editorial!
Btw, is 442A with the cards and instance of some well known NP-complete problem? First I was thinking set-cover, but that doesn't really fit. Maybe there is some other graph way to formulate it?
Someone please explain Div2 problem B.
Check my solution at : here First add "." k-times after input string and bruteforce find optimal start character of tandem and length of it in new string.
For problem E you can also use Voronoi diagrams.
1) Build the diagram of the whole set, call it V
2) For each point p, build the diagram of its neighbors in V, call it N.
3) Use the vertices of N as candidate solutions.
In step 2) we're looking at what happens when p is the closest point, and it's easy to see that the optimal point in that case has to be one of the vertices of N (since they are the most distant from surrounding points).
Since the number of points is not too big, you can use the simple half-plane intersection algorithm to find a Voronoi cell in O(n log n), and the whole diagram in O(n^2 log n).
It's crucial to look only at the neighboring points of p in step 2 (looking at the diagram of all points except p would also be correct, but slow), as otherwise you'll be recomputing the whole diagram n times. This way the complexity of the whole thing is still O(n^2 log n) (if I'm not mistaken).
can you provide me some links to this simple voronoi building algorithm? All I could find in my researches was an O(n^4) algorithm and the reaaally big O(n log n) sweep line one.
EDIT: nvm, when I searched for "O(N^2 log(N)) voronoi" this popped out: http://web.mit.edu/~ecprice/acm/acm08/notebook.html#file7
C can also be solved in O(n):
While there are elements ai such that ai - 1 ≥ ai and ai ≤ ai + 1, we always want to remove ai before removing ai - 1 or ai + 1. (When doing the comparisons, we assume a0 = an + 1 = 0.) We can maintain a queue of elements with this property, and delete those elements. After removing an element, we check if we need to push one of its neighbors onto the queue. Once there are no more elements like this, we have a bitonic sequence, which is easy to deal with.
My code implementing this algorithm is here.
I don't know how I solved D(div 1. B) but I didn't realise how to solve B nor C... Kind of weird.
Same here! It's weird, it seemed like easy elementary school probability math. Although div2b was really easy, I just forgot that one if-clause there.
D wasn't that obvious to me, lol and i've never seen this kind of probability problem in elementary school, unfortunately. B was way easier, but I was afraid of being hacked from the moment i send it (didn't bother to check for corner cases)
Can u ans(ans explain) for test case Q.4(Div 2)
3
0.087234 0.075148 0.033833
first sort the probabilities.. then suppose they are a,b,c in sorted order 1.Take a*(1-b)*(1-c)+b*(1-a)*(1-c)+c*(1-b)*(1-a) which is prob of getting one of them at a time. 2.Then leave the smallest probability a,then find b*(1-c)+c*(1-b) 3.Then leave prob b and take c. 4.Take the best value(closest to one) among the three calculated above. Using this u can calculate the answer for ur test case.
I think it is better to include a standard solution link after each problem's editorial.
Exactly! I just don't understand the explanation for problem B div2 :(
I hope this helps!
Thanks a lot! I see that your algorithm is as same as thee editorial. I'm understanding it better.
I didn't understood how to solve 443B can someone explain how to solve with example.
my explanation based on the editorial:
?k times to the end of string to get a new string. Lets call its.j=length(s) div 2.i=1.copy(s,i,2*j). Let divide the substring into 2 strings:string x=copy(s,i,j)andstring y=copy(s,i+j,j).xandy, we replace every?in stringywith the character in respective position of stringx. After the replacement, ifx=ythen we have a tandem string; if not, increaseiby1and go back to Step 4.i>(length(s)-2*j+1)and we cannot find tandem substring with length2*jwe decreasejby1and go back to Step 3.my code: 6926507
sorry for my limited english :)
Nice Competition
@ m3kAnix
Explanation of problem (div2)B: Let's see an example. The input string is "abc" and the value of k is 5. Now we have to check all possible string for tandem repeat. New length of the string is 3+5=8. so let's assume our new string "abc?????" now when we check for tandem repeat and we encounter position 1 and position 4 we get 'a' and '?' .We take that as a match. if we encounter 'b' and '?' then we also take that as a match. '?' can be any character, that's the point.
Div 2, Q 4
Getting WA on test case 12 i.e
3
0.087234 0.075148 0.033833
According to me, ans should be 0.149271078736(taking first 2 elements together) but its 0.172781711023(according to judge)
Any suggestion plz ??
if in your last sumbission you change line
to
It will get AC.
Got my mistake Thanks a lot...!!!
I don't get div2 E (div1 C) explanation. It states that we need to choose the minimal alive element, excluding the borders, but test case 3 already shows it's not true. Deleting minimal elements first results in the answer "3". Am I missing something?
I also did not get it either.
But from this solution what I get is, at first I've to choose
Aisuch thatAi-1 >= Ai <= Ai+1Then we sort the remaining and choose all except bigger two of them, as we have to take minimum value.how do u type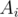 (with subscript) within the
(with subscript) within the
Inline?I use HTML < sub > tag.
subtag
test:
sumi = sumi-1 + aithanks, i figured it out. :)
This solution implements the idea described in the tutorial. I'm still working to understand it.
Thanks. Now I understand the tutorial. This is exaclty the described solution.
I will try to explain here.
Now,Lets see. There can be repeated elements. Like 3 can be in many positions. So to identify each appearance we need a touple like (value,pos) or (pos,value) . Each touple will be unique.
We consider (val,pos) in increasing order.[As explained in the editorial. This is a simple proof by contradaction. I can explain it further if needed.]
The main loop runs for (n-2) times. In each iteration it edits the ans by (val-cero)*(n-i-2). Here cero is SO FAR seen lowest VAL. And (n-i-2) is its contribution.
I tried to put as much detail as possible in this submission. Hope it helps :)
14996334
Agreed, i also find this as wrong solution (or maybe i just dont understand something ?). I could say it would work if removing something at the first or last place of an array would give points for its only neighbour, but we get nothing so it's actually wrong solution.
Can someone explain why "Boris can describe all of his cards iff he can distinguish all pairs of different cards" (Div1 A/Div2 C)?
I don't have idea why the grader and custom output different. Could someone help me on this?
Submission : 6930710
i didn't understand problem C div 2 at all, can anyone please help me to understand how to solve this problems?
Thanks :)
Basically you can try every combination of hints. There are 2^10 = 1024 combinations. (Note that the order does not matter.)
D: In fact, the asymptotic run-time of each operation is O(1); there are at most N nodes with DP value at least 1, N/2 with DP value at least 2, ..., 1 node with DP value at least log(N), so the sum is 2N, not N log N.
Not true. Consider the following tree:
Simple path of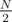 nodes:
nodes:
And full binary tree of size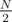 rooted at vertex (N / 2).
rooted at vertex (N / 2).
Here the DP values of the first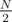 nodes will be
nodes will be  .
.
you are right. my bad.
Would anyone please discuss the solution with an example of 442A - Borya and Hanabi ? I am finding
"He can do it iff he can distinguish all pairs of different cards. He can do it if somebody told at least one distinction. It can be a hint about color of one of cards (if they don't have same one) or it can be hint about value of some card."
this portion hard to understand. Any help would be appreciated.
He can only distinguish two cards (say A and B) if there was a hint that was applicable to A but not to B or the other way round.
Now when you start brute forcing through all possible sets of hints, for every set of hints see which card gets pointed at by which hint. If for two different cards the hints that pointed towards them are different only then can he tell that the cards are different otherwise he can't and that particular set of hints is not enough to tell all cards apart.
What about if there are multiple cards of same colour and value? Would you mind clarifying it ?
INPUT :
3G4 G4 G4 A5If you can distinguish one G4 from A5 then you can distinguish all G4's from A5. Let me try an example: if you're currently testing whether the set of hints {G,2,3} works or not then
1st G4 is pointed at by hint {G}
2nd G4 is pointed at by hint {G}
3rd G4 is pointed at by hint {G}
A5 is not pointed at by any hint among {G,2,3} therefore {}
Now, using the hints that each card is pointed at, you can distinguish between the first three cards and the fourth one as they have different sets of hints pointing at them. You cannot however distinguish between the first three cards. Now if the first three cards are equal then this condition is fine as any hint that points at card 1 will also point at the other two. However, if the first three cards are different then we have a problem.
let us try out the set of hints {1,2,3} for G1 G1 R1 R2
pointing at card 1 {1}
card 2 {1}
card 3 {1}
card 4 {2}
We can tell apart the 4th card from the others but we can't distinguish between the first three cards. As the first three cards are not the same, therefore, this set of hints is not enough to determine each card.
Can someone please explain the 5th test case in problem B DIV2
The tandem repeat would be like this :
ayiabc ayiabc aMaximum length is 12. So the answer is 12.
Can someone please explain Div2 E (Div1 C) explanation? It says choose the minimum alive element. But following this in test case 3 (1 2 3 4 5), we get a wrong answer = 3.
can anybody explain the solution of problem E div 1.
This solution for E is very interesting. Can anyone explain me in which kind of situations is this random walk applicable ?
Can anyone explain me in detail How to solve Borya and Hanabi using BitMasking or Is their any other approach to solve this problem. Thank You In Advance !!
start with the bitmask = 0 and add one to it until it reaches 2^10-1, that means you'll have all bitmasks from 000000000 to 111111111, which are all the different combinations of tips (first bit to fifth: tips for indexes (1, 2, 3, 4, 5); sixth to tenth: tips for letters (R,G,B,Y,W)).
now, all you have to do is check if the tips you have on (bit on bitmask = 1) are enough in each iteration and get the minimum number of "on" bits. you can check if the tips are enough by just comparing each card to each other. There are 3 types of pairs of cards: 1) Different Indexes (1R and 2R) You need a tip for either index 1 or index 2 (tips for colors are not important) 2) Different Colors (1R and 1B) You need a tip for either color R or color B (tips for indexes are not important) 3) Different Indexes and Different colors (1R and 2B) You either need a tip for 1, 2, R or B (only one is enough) 4) Cards are the same (1R and 1R) You don't need any tips
If you have a valid tip for each pair of cards, then the bitmask is a valid choice of tips, and you can make ans = min(ans, number of 1 bits in bitmask)
Okaye . . Now I got it .. Thanks for this great explanation .. @caioaao
You're welcome! I know how frustrating it can be when we don't understand an old editorial and there's no one there to answer your doubts, so I'm glad I could help :D
Yups Bro. . I totally agree with you. It happens when you are in learning phase and Sometimes we unable to understand the editorial as well as other Coder's code . btw this time I'm lucky that you helped me. :-)
thanks for this great explanation :)
Can anyone explain me in detail How to solve div 1 problem C Artem and Array? thanks in advance.
443A I solved it by iterating the given string and set elements in array of ints equal to size of English letters, and finally sum all the 1s in the array. I guess its of O(n + k) where k = 26, and for n >> k, its O(n). The solution refered to here will cost more than that as I will iterate over the string 26 times O ( k * n ).
As n is smaller than 1000 and k is 26, the difference between O(k * n) and O(k + n) isn't very big and both solutions work very fast. I described solution which in my opinion is easier to code.
Hi isn't problem E Gena and Second Distance a typical denaulay trianglution problem? find denaulay trianglution of N points and compute the maximum circumradius of each denalay triangles?
As you correctly mentioned in russian-language thread n*log(n) delaunay triangulation is not very easy thing, and it's hard to write it during the competition (but you can solve this task with some modification of it). The solution I described in the editorial can be written in just 20-30 minutes.
I moved from Topcoder to practice here as the quality of their tutorials drastically go down after SRM 600.
I started with CF 253 and problem C. What's this shit???? I don't understand even a single word of this fucking tutorial. There are lots of grammatical mistakes and typos with no proof!