Solution:7139559
Because rewards of one type can be on one shelf, lets calculate number of cups — a and number of medals — b. Minimum number of shelves that will be required for all cups can be found by formula (a + 5 - 1) / 5. The same with shelves with medals: (b + 10 - 1) / 10. If sum of this two values more than n then answer is "NO" and "YES" otherwise.
Solution:7139584
Consider each case separately. If we use only suffix automaton then s transform to some of its subsequence. Checking that t is a subsequence of s can be performed in different ways. Easiest and fastest — well-known two pointers method. In case of using suffix array we can get every permutation of s. If it is not obvious for you, try to think. Thus, s and t must be anagrams. If we count number of each letter in each string, we can check this. If every letter appears in s the same times as in t then words are anagrams. In case of using both structures strategy is: remove some letters and shuffle the rest. It is possible if every letter appears in s not less times than in t. Otherwise it is impossible to make t from s. Total complexity O(|s| + |t| + 26).
Solution:7139610
To solve this problem we need to understand some little things. First, every horizontally stroke must be as widely as possible. Second, under every horizontally stroke should be only horizontally strokes. So, if bottom of fence painted by horizontally stroke then number of this strokes must at least min(a1, a2, ..., an). These strokes maybe divides fence into some unpainted disconnected parts. For all of these parts we need to sum they answers. Now its clearly that solution is recursive. It takes segment [l, r] and height of painted bottom h. But we must not forget about situation when all planks painted with vertically strokes. In this case answer must be limited by r - l + 1 (length of segment). With given constrains of n we can find minimum on segment by looking all the elements from segment. Complexity in this case will be O(n2). But if we use for example segment tree, we can achieve O(nlogn) complexity.
Solution:7139620
Solution is binary search by answer. We need to find largest x such that amount of numbers from table, least than x, is strictly less than k. To calculate this count we sum counts from rows. In i th row there will be 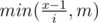 . Total complexity is O(nlog(nm)).
. Total complexity is O(nlog(nm)).
Solution:7139644
Learn how to transform Xi into Xi + 1. For this we need to concatenate lists of divisors for all elements of Xi. To do this efficiently, precalculate divisors of X (because for every i Xi consist of its divisors). It can be done by well-known method with 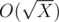 complexity. How to calculate divisors of divisors? Need to know that for the given constrains for X maximum number of divisors D(X) will be 6720 (in the number 963761198400), so divisors of divisors can be calculated in O(D2(X)) time. With this lists we can transform Xi into Xi + 1 in O(N) time, were N = 105 — is the limit of numbers in output. Now learn how to transform Xi into X2i. What says Xi? Besides what would be X after i steps, it can tell where goes everyone divisor of X after i - 1 steps. Actually, Xi is concatenation of all Yi - 1, where Y is divisor of X. For example, 103 = [1, 1, 1, 2, 1, 1, 5, 1, 1, 2, 1, 5, 1, 2, 5, 10] = [1] + [1, 1, 2] + [1, 1, 5] + [1, 1, 2, 1, 5, 1, 2, 5, 10] = 12 + 22 + 52 + 102. How to know which segment corresponds for some Y? Lets pos(Y) be the first index of Y in Xi. Then needed segment starts from pos(prev(Y)) + 1 and ends in pos(Y), where prev(Y) is previous divisor before Y in sorted list of divisors. So, to make X2i from Xi we need to know where goes every element from Xi after i steps. We know all its divisors — it is one step, and for every divisor we know where it goes after i - 1 step. Thus, we again need to concatenate some segments in correct order. It also can be done in O(N) time. How to find now Xk for every k? The method is similar as fast exponentiation:
complexity. How to calculate divisors of divisors? Need to know that for the given constrains for X maximum number of divisors D(X) will be 6720 (in the number 963761198400), so divisors of divisors can be calculated in O(D2(X)) time. With this lists we can transform Xi into Xi + 1 in O(N) time, were N = 105 — is the limit of numbers in output. Now learn how to transform Xi into X2i. What says Xi? Besides what would be X after i steps, it can tell where goes everyone divisor of X after i - 1 steps. Actually, Xi is concatenation of all Yi - 1, where Y is divisor of X. For example, 103 = [1, 1, 1, 2, 1, 1, 5, 1, 1, 2, 1, 5, 1, 2, 5, 10] = [1] + [1, 1, 2] + [1, 1, 5] + [1, 1, 2, 1, 5, 1, 2, 5, 10] = 12 + 22 + 52 + 102. How to know which segment corresponds for some Y? Lets pos(Y) be the first index of Y in Xi. Then needed segment starts from pos(prev(Y)) + 1 and ends in pos(Y), where prev(Y) is previous divisor before Y in sorted list of divisors. So, to make X2i from Xi we need to know where goes every element from Xi after i steps. We know all its divisors — it is one step, and for every divisor we know where it goes after i - 1 step. Thus, we again need to concatenate some segments in correct order. It also can be done in O(N) time. How to find now Xk for every k? The method is similar as fast exponentiation:
Xk = [X] when k = 0,
if k is odd then transform Xk - 1 to Xk,
if k is even then transform Xk / 2 to Xk.
This method takes O(logk) iterations. And one small trick: obviously that for X > 1 Xk starts from k ones, so k can be limited by N. Total complexity of solution is 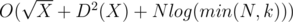 .
.











great contest!
Thanks, man.
lol, comment from someone who didn't participate. btw, problem C was great :)
he could be one of those gray guys...
Question C was awesome..!!
i
first of all you should print YES instead of Yes
Sorry, but in your code nothing is right..
So u red now?
~~~~~ Your code here... ~~~~~simply everything with this code is wrong. You have so many variables lol
I think you should check your coding convention before public you code
it was a really great contest and it's a pity that i don't have time to read Problem E.
great contest! The problem is very nice! Thank you! what a pity it is DIV2 only.
is this round rated or not? i can't see the change of my rating.
div2 is rated, div1 is unrated
can anybody please tell whats wrong with my approch in C ... please help .. http://codeforces.com/contest/448/submission/7138159
try this case :
10
1 3 3 2 2 3 3 2 1 1
i am getting 4 as the output ... is it right??
Yes.
10 5 5 5 5 5 2 5 5 5 5 the answer should be 8.
Please can anyone give me more details for problem C solution?? how is it O(n²)?
in each segment [l,r] you should find minimum element O(n) and by dividing you have at most n segment to solve
assume this test:
9
9 8 7 6 5 4 3 2 1
You have to track h: the height of painted bottom too no?? and 1<h<10^9 :/
the solution's order is not related to h
assume you got [1,n] , there is two cases : 1. you paint horizontally : in this case the number of strokes is min(a[1,n])
and next you should solve some new segments 2. you paint them all vertically
5 1 2 2 1 2
if you paint horizontally you have these segments : [2,3] and [5,5] then you should solve them seperately
5 8 7 6 5 4
you first solve [1,5] >> [1,4] >> [1,3] >> [1,2] >> [1,1]
Thank you for the time you gave me now i've got it :D
Just a small grammar mistake: (problem D) "In i th row their will be..." I think you meant "there." But anyway, great tutorial (I'm totally not a grammar nazi :D).
How can i view solution of these problems.I am new to codeforces.
When you enter the contest standings, you can see anybody's solution to any problem.
great contest..problems are very interesting...
please anyone explain briefly how to solve problem C .... i didn't understood the editorial. please!!!
Here's a general idea: Suppose we have a recursive function
f(l, r)that gives us the minimum number of ways to paint the fence (And hence the solution that we are looking for isf(1,n)). Note that you can paint the fence using only vertical strokes, which takes r-l+1 strokes and hencef(l,r) <= r - l + 1.In order to use the horizontal strokes optimally, we need to paint the fence from the bottom most row to the maximum row that we can paint using one stroke. For example, for the configuration
[2, 2, 3, 4, 2, 3, 2], it is only optimal if we paint the bottom 2 rows if we were to use horizontal strokes at all. Otherwise we will be better off using vertical strokes.Using the same example, upon painting the bottom two rows, we are left with the array
[0, 0, 1, 2, 0, 1, 0]. Now we call the recursive function onf(3, 4)andf(6, 6)to paint what is remaining on the fence. Of course, we need to remember the amount of rows which we have already painted when we recurse. Here's a pseudocode for the recursive function.something like this: 7134060
Thank for your clear explanation! Small typo: f(l,r) <= r-l+1, due to the definition of f(l,r) as the minimum number of ways.
Brilliant explanation. Much better than what was given in editorial.
Trying to understand solution of 448C - Painting Fence. oversolver does this part build the segment tree iteratively?
Yes !. You can also build segment tree with recursion but each node should keep track the index of minimum elements in range. 7140283
I know that segment tree requires O(4 * n) space but he's using an array of size n. How is that possible?
Since you only need to do queries (and no updates) you can use sparse data table, that can be constructed iteratively. Sparse data table
Thanks. Down-vote logic is a mess on this website.
Nice problems, thanks you !.
Can anyone please elaborate a bit more on the approach to solve problem D ?
Assuming that you already know binary search, the idea is simple, at least for me. The multiplication table looks like:
Let f(x) the number of elements on the multiplication table that are less than x. f can be compute by iterating each row and check how many numbers are less than x, that is (x-1)/i, but you have to remember that you only have m columns, so you take min(m,(x-1)/i). With binary search we want to find largest x so that f(x) < k. Hope it was clear
Great, Thanks for your neat explanation
Thank you for clearing my doubt and a neat explaination. +1
Thanks a lot pachon, I wasn't so sure where did the (x-1)/i pop up from until I saw your table. :D
Thanks for clarification. But i did not understand how l-1 is our answer because l=1 and h = n*m+1. And all elements between this range are not part of multiplicable table.
Can you point out to what code are you referring to?
In my case, back then I submitted this.
I use variables
lo, hivariables for thewhileloop.I would say that in binary search you need to find a range that allows you to handle all possible cases and still returns the correct answer. Depending on your conditions you can use a
lovariable with0, 1, -INF, -1, ...the sames hold forhivariable.In this problem, I used the
hi = n*m + 1just to handle some cases like1 1 1. Also if you check other participant's code you can see that in binary search is common to returnlo - 1if after a halving range operation you are setting yourlo = mid + 1, conversely you should returnlo + 1if you setlo = mid - 1.can someone tell me why my approach is not correct. I decrease the heights of the plank in each stroke. First , I can give a horizontal or vertical strip. Now , from pos 1 I find the first segment whose left and right planks are completely painted. at first it is the whole segment 1...n . Now I check , if the maximum height in this segment is less than (r-l) , then I give a horizontal stroke and I subtract 1 from all the planks in the segment. Or else I stroke the highest plank vertically , and set its height to INF. now I continue this until I have every plank either 0 or INF. Here is my code ,7140267
Contest was really great! I enjoyed the problem D. However, I did not understand the code of the problem C, maybe someone has solution without segment tree?
There is a recursive solution using divide and conquer as mentioned by the author. I solved it using this approach My submission : 7140132
There was a o(n^2) DP solution.
If you dont like segment tree, just replace
rmq(l,r)tomin_element(a+l,a+r+1)-ain my solution:)Oh, thanks. Now I understood)
oversolver thank you for these interesting problems, I don't understand why we're seeking for the minimum element in the segment
instead of
any clarification would be so appreciated, thanks in advance
All its ok, we find minimun in [l,r], it is just signature of standart c++ function like
sortorreverse, right bound always is not included.Hi there.
about problem D. what is the necessity that the answer from binary search could be built by two integer 1<=i<=n & 1<=j<=m ?
it may be a large prime number(larger than n , m) .
I came up with a O(n^2) DP solution for C,suboptimal asymptotics but may be simpler to code. Let v[pos][h] be the minimum # of strokes to paint from stick 'pos' onwards and with horizontal bars coming from the left up to height h. Then:
-If h>height[pos] h=height[pos] (bars higher than height[pos] stop)
-Now the solution is simply the minimum of:
painting vertical:1+v[pos+1][h]
painting horizontal (only if height[pos]<n, it can't be the solution): height[pos]-h+v[pos+1][height[pos]]
yoones.rezaei did you do the same?
In problem C here is a my code on contest. http://codeforces.com/contest/448/submission/7136746
My min variable is global!
Just changed it to local, i took accepted. http://codeforces.com/contest/448/submission/7142429
What a pity :(
Nice implementation.
You really made my day, thanks gentleman!
Is it possible to solve C using a O(nlogn) greedy method?
I'm not sure whether there's a smaller counterexample, but
5 4 5 4 5 4 5breaks your solution. The best solution is to paint all vertical strokes (7 strokes), but your solution will begin by painting four horizontal strokes at the bottom followed by four more to clear the "spikes" (8 strokes).For problem D,I have an another idea.But it may be wrong. We can divide the number into n blocks. In block i,the numbers are bigger than i*m and smaller than (i+1)*m; We can know the k-th largest number is in which block. Then we sort the number int the block and find the number. The complexity may be O(mlogn+mlogm) It is not as good as solution but I think it's also an idea. Please think it carefully instead of disliking it simply.
I dont understand this solution from this part
and find the numberErr...Maybe my English is too poor T_T. It means like this: 1 2 3 4, 2 4 6 8, 3 6 9 12, The number in first block is 1 2 2 3 3,in second block is 4 6 6.And in third block is 8 9 12. We can find the number in each line which is in the block like what you said. And know the k-th largest number is in which block. Then we copy them to an array and sort.
oh, yes, now this patr i understand.
but how you find kth number in block? for example first block (with n=m=500000) contains 6638449 elements. Second — about 6 millions.
Oh,It seems that I am wrong. I didn't realize there will be so many numbers in a block in the contest. I only think it will be similar to m.
It's really a good problem.Thank you very much!
Original idea in edit. Saw that my idea was completely wrong, lol
just to be clear that I know there are lots of improvements that can be done (linear sort on diagonals, binary search to find the diagonal in which the item stands), but i thought an O(m*log m) solution would be fine and easier to code in contest time
Regarding the problem D, I still don't understand why in the solution code we don't need to check if the number is in the multiplication table. Can someone please explain?
There are n*m numbers in the multiplication table. k <= n*m . So the number must be in the multiplication table. Tip:if a*b=c*d,they can be counted twice instead of only once.
Take the 2x3 table, then 5 <= 2*3 is not in the table, isn't it? My question is about the answer from binary search, i.e. l-1. Why is it always in the table?
Suppose that we have found the answer x that is not in the table. This element has the L numbers less than it. But since it is not in the table, then there is a greater element with the same number of smaller elements L, and thus a contradiction, because we have to find the maximum such x.
Oh,yes. But I think it's not a problem. If you search 5.you will only let l=5 or r=5 instead of printing 5. In binary search,l and r may be not in the table at first.but they will be right in the end.
I'm not sure if I understand your comments correctly. But, we can prove the binary search solution, i.e. l-1 is included in the table as follows: At the end of binary search loop, l is the number that satisfies count(l) >= k and count(l-1) <= k-1, then l-1 has to be included in the table, otherwise those two conditions never hold. That means, l-1 is in the table and count(l-1) = k-1. Then l-1 is the k-largest number.
Please someone explain the solution of problem D properly. Can't understand a thing. :(
Here you go: http://codeforces.com/blog/entry/13063#comment-178268
Thanks a lot kayesjay! Understood. :D
In 448E - Divisors, can someone explain better how to make X2i from Xi? I don't understand the wording in the editorial!
"Actually, Xi is concatenation of all Yi - 1, where Y is divisor of X. For example, 103 = [1,1,1,2,1,1,5,1,1,2,1,5,1,2,5,10] = [1] + [1,1,2] + [1,1,5] + [1,1,2,1,5,1,2,5,10] = 12 + 22 + 52 + 102."
As I see it, this is the crux of the problem. I'll try to put this in different words:
Let the divisors of X be D1, D2,.., Dk, in increasing order. So, X1 = [D1, D2, .., Dk] Now, you can take each of these Di separately, transform them i - 1 times independently to get (D1)i - 1, (D2)i - 1, etc and then concatenate those to get Xi. ie, Xi = (D1)i - 1 + (D2)i - 1 + .. + (Dk)i - 1
Now, suppose you have Xi, and you also know which segments correspond to (D1)i - 1, which correspond to (D2)i - 1, etc. Now, you want to get X2i. First, you transform Xi to Xi + 1. Now, you take the first element from Xi + 1. This will be a divisor of X. Let it be Dj. From the previous step, you already know (Dj)i - 1. So, take that and shove it into X2i. Now, take the second element of Xi + 1 and repeat the same. Keep doing this till you get the first 105 elements of X2i.
Now, all we need to do is figure out is which segment of Xi corresponds to (D1)i - 1, etc. That is explained here: "How to know which segment corresponds for some Y? Lets pos(Y) be the first index of Y in Xi. Then needed segment starts from pos(prev(Y)) + 1 and ends in pos(Y), where prev(Y) is previous divisor before Y in sorted list of divisors." Replace Y with Dj and prev(Y) with Dj - 1. I think this part is explained clearly in the editorial itself. See the 10 example.
Solving B using regexps ( O(|s|*|t|)+ ), language — Perl: 7157269
Well,Problem 448D — Multiplication Table. I've got binary search solution for python. But it is Time limit exceeded. Can't we use python ? My solution ID 7400257
My solution ID:7400257
Excuse me, but how we can achieve O(NlogN) in Painting Fence. Yeah, with segment tree we can find minimum in interval[l,r], but (atleast I think so) we need to have indexes of all the minimums inside that interval, so we'll have to iterate that, which bring us to complexity of O(N^2). Am i wrong?
Thanks in advance. :)
Firstly, we need only one index. After finding that index we call recursion to [L,ind-1] and [ind+1,R]. If you draw recursion tree with these segments you will see that tree have exactly N vertices. In every vertex we need O(N) or O(logN) time for search.
I wonder how you found that 963761198400 in 448E - Divisors?
It is just a typical problem :)
Editorials like these with their incomprehensible English make me want to kill the editorial writer,,, slowly and painfully.
Good luck
Great contest though. Cheers.
give me — please :)
a very silly contest
My solution
Can anyone explain to me what is wrong with my solution?? Need help plz.
How do you define 'k-th largest number' ?
In sample: 2 3 4
the matrix is:
1 2 3
2 4 6
all sorted numbers are: 6, 4, 3, 2, 2, 1
the 1st largest number is 6, the 2nd largest number is 4, the 3rd largest number is 3, the 4th largest number is 2, so the answer should be 2. Why the answer is 3?
Wow, yeah, so the English in this problem was absolutely terrible. It is actually looking for the k-th smallest number, not the k-th largest. It describes picking the k-th number from a non-decreasing list of the integers, but that is literally what k-th smallest means. Fortunately, if you just do k = n*m+1-k in the beginning, it should fix your code, but it gave me trouble for a good while trying to understand what it meant.
All the 5 que are very fantastic. Especially last 3 que are very very great.
Salute for question setter. Thank you.
Doubt regarding 448D- Multiplication Table
In question Multiplication table, what happens when the binary search chooses a number that does not belong in the multiplication table matrix of m*n? How does the tutorial solution escape that situation to give the correct result?
Didn't understand this either... the number could easily be a prime greater than max(n,m).
The number can't be a prime. All elements in the table, except for row
(1, j)and column(i, 1)where i,j are within the range (1 ... n) and (1 ... m) respectively, are a product of two numbersi*jand the problem asks for thek-thout of all of them.Very Interesting: my idea for Problem E was completely different from the editorial. I noticed that for $$$k\leq10^3$$$, we can just do naive brute force and it will easily pass ($$$10^8$$$ operations). For $$$k>10^5$$$, we can just print $$$10^5$$$ ones.
The interesting case is when $$$10^3\leq k\leq 10^5$$$. Here, I observed that it is always enough to consider only all factors upto the first non-prime factor of $$$X$$$. And we can easily deduce the array for primes, and also for composite numbers which are either just product of two primes or $$$p^2$$$, for some prime $$$p$$$. It is exactly composite numbers of this forms which are the first non-prime factor of any number. The rest is just concatenation.
Here is my solution: 97098735
Can anyone explain why TLE occurs in the following code for problem C?
if (p1<=n-1) ans+=rec_func(p1,n-1,h+mini);you needrinstead ofn-1