From a grid of size n * m, if we remove an intersection point, then the grid after removing the sticks passing through it, will of size n - 1, m - 1.
Notice when the grid consists of a single horizontal stick and m vertical sticks, If we pick any intersection point, then the updated grid will be only made of vertical sticks. You can see that there is no intersection point in the grid now.
So
ans(n, m) = ans(n - 1, m - 1) ^ 1.
ans(1, * ) = 1
ans( * , 1) = 1
So we can notice that answer will depend on the parity of minimum(m, n).
You can prove it using the previous equations. You can also check this by seeing the pattern.
So finally if min(n, m) is odd, then Akshat will win. Otherwise Malvika will win.
You can also observe that "players will play optimally" is useless in this case.
Complexity : O(1)
Solution codes
Note that if from a given sorted array, if reverse a segment, then the remaining array will be arranged in following way. First increasing sequence, then decreasing, then again increasing.
You can find the first position where the sequences start decreasing from the beginning. Call it L.
You can find the first position where the sequences start increasing from the end. Call it R.
Now we just need to reverse the segment between a[L] to a[R].
Here is outline of my solution which is easy to implement. First I map larger numbers to numbers strictly in the range 1, n.
As all the numbers are distinct, no two numbers in the mapping will be equal too.
Let us define L to be smallest index such that A[i]! = i.
Let us also define R to be largest index such that A[i]! = i.
Note that if there is no such L and R, it means that array is sorted already. So answer will be "yes", we can simply reverse any of the 1 length consecutive segment.
Otherwise we will simply reverse the array from [L, R]. After the reversal, we will check whether the array is sorted or not.
Complexity: O(nlogn)
Solution codes
451C - Predict Outcome of the Game
Let x1 be number of wins of first team in the first k games.
Let x2 be number of wins of second team in the first k games.
Let x3 be number of wins of third team in the first k games.
Note that x1 + x2 + x3 = k ---(1)
|x1 - x2| = d1. — (a)
|x2 - x3| = d2. — (b)
Note that |x| can be x and -x depending on the sign of x.
Case 1: Assume that x1 > x2 and x2 > x3.
x1 - x2 = d1 ---(2)
x2 - x3 = d2 ---(3)
Adding 1 and 2, we get
2x1 + x3 = d1 + k --(4)
Adding 2 and 3, we get
x1 - x3 = d1 + d2 ---(5).
Now solve (4) and (5), we will get values of x1 and x3. By those values, compute value of x2. Now we should check the constraints that x1 ≥ x2 and x2 ≥ 3.
Now comes the most important part. Number of wins at the end of each team should be n / 3. So if n is not divisible by 3, then our answer will be definitely "no".
Note that if all of the x1, x2, x3 are ≤ n / 3, then we can have the remaining matches in such a way that final numbers of wins of each team should be equal.
Now you have to take 4 such cases. Implementing such cases in 4 if-else statements could incur errors in implementation. You can check my code to understand a simple way to implement it.
I will explain idea of my code briefly, basically equation (a) and (b) can be opened with either positive or negative sign due to modulus.
So if our sign is negative we will change d1 to be - d1. So if we solve a single equation and replace d1 by - d1, we can get solution for the second case.
All the cases can be dealt in such way. Please see my code for more details.
Complexity: O(1) per test case.
Solution codes
Merging Step: We have to convert string like "aaaabbbaabaaa" into "ababa".
Important Observation
A substring made of the string will be a "good" palindrome if their starting and ending characters are same. If the starting and ending characters are same, then the middle characters after merging will be alternating between 'a' and 'b'. eg. "abaa" is not a palindrome, but it is a good palindrome. After merging step it becomes "aba". Note that in the string left after merging, the consecutive characters will alternate between 'a' and 'b'.
So if we are currently at the ith character, then we can have to simply check how many positions we have encountered upto now having the same character as that of ith. For counting even and odd separately, we can make count of a's and b's at even and odd positions.
So if we are at ith position, for counting even good palindromes, you just need to add count of number of characters a's at odd position. For counting odd good palindromes, you just need to add count of number of characters a's at even position.
Complexity: O(n) where n is length of string s.
Solution codes
Note that you can also consult following comment for alternate editorial.
The number of ways to choose N items out of R groups where each item in a group is identical is equal to the number of integral solutions to x1 + x2 + x3...xR = N, where 0 ≤ xi ≤ Li, where Li is the number of items in ith group. Number of integral solutions are coefficient of xN in [Product of (1 + x + x * x + ...xLi) over all $i$].
You need to find coefficient of xs in (1 + x + x2 + x3 + + ..xf1) * * * (1 + x + x2 + x3 + + ..xfn).
Using sum of Geometric progression we can say that (1 + x + x2 + x3 + + ..xf1) = (1 - x(f1 + 1)) / (1 - x).
Substituting in the expression, we get (1 - x(f1 + 1)) / (1 - x) * * * (1 - x(fn + 1)) / (1 - x).
= (1 - x(f1 + 1)) * .. * (1 - x(fn + 1)) * (1 - x)( - n).
Now we can find xs in (1 - x) - n easily. It is 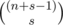 .
.
You can have a look at following link. to understand it better.
So now as s is large, we can not afford to iterate over s.
But n is small, we notice that (1 - x(f1 + 1)) * .. * (1 - x(fn + 1)) can have at most 2n terms.
So we will simply find all those terms, they can be very easily computed by maintaining a vector<pair<int, int> > containing pairs of coefficients and their corresponding powers. You can write a recursive function for doing this.
How to find 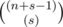 % p. As n + s - 1 is large and s is very small. You can use lucas's theorem. If you understand lucas's theorem, you can note that we simply have to compute
% p. As n + s - 1 is large and s is very small. You can use lucas's theorem. If you understand lucas's theorem, you can note that we simply have to compute 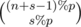 .
.
Complexity: O(n * 2n).
Another solution based on inclusion exclusion principle.
Please see the following comments to get the complete idea.
Comment 1
Comment 2
Comment 3
Solution codes











All the "solution codes" are of a previous contest.
Please, fix your links to solutions. They are leading to 439A problem now
Solution link for the problem "Sort The Array" is broken.
are you sure that your solution link for 451C
it seems 439A
Your definitions of x2 and x3 in 451C are slightly incorrect.
Solution of problem E is still not clear to me :( .
So number of ways to choose N items out of R groups where each item in a group is identical is equal to the number of integral solutions to x_1+x_2+x_3...x_R=N, where x_i <= L_i, where L_i is the number of items in i'th group. Number of integral solutions are coefficient of x^N in [Product of (1+x+x*x+...x^{L_i}) over all i].
I don't undestand this "Number of integral solutions are coefficient of x^N in [Product of (1+x+x*x+...x^{L_i}) over all i]."
Please, could you give example of this coefficient or something else for second sample test from this problem? =)
You might need to google "Generating Function".Problem E is a kind of problem of theory "Generating Function".Beside it needs the theory "Binomial theorem" too.
number of integral solutions to x1+x2=4. where x1<=4 and x2<=1. will be coeff. of x^4 in (1+x+x^2+x^3+x^4)*(1+x). it's quite intuitive if you think over it.
Let x1 be number of wins of first team in the first k games. Let x2 be number of wins of first team in the first k games. Let x3 be number of wins of first team in the first k games.
first, second, third.....
In E, why is lucas required? I need to find C(N+R-1,R-1) where N<=20 and R is very high. numerator=product of i from i=r+1 to n+r-1. denominator=product of i from 1 to n-1. keeping care of overflow, we can calculate C(N+R-1,R-1) using inverse modulo.
Its merely used for analysis that you can simply compute n%p C s%p instead of computing nCs % p.
Can you give the proof?
sorry!I see the link!
For E, You can Simply use Inclusion-Exclusion Principle :)
Yes, ofcourse. Most of the times we miss simple solutions in look of harder ones.
Can you please explain how we can use Inclustion-Exclusion principal in this problem?
As you know, The number of solutions to x1 + x2 + ... + xn = k is C(n + k - 1, n - 1). And if we have some xi > = d > 0, we can subtract d from k and the number of solutions is C(n + k - d - 1, n - 1). So We use Inclusion-Exclusion Principle Here and a simple iteration over 2n ways of including or excluding number of flowers on each box. Excluding means xi > Fi. And there are some hassle of calculating C(n, r) for a big n that can be easily solved using mentioned ways :)
Can you add a little more explaination to ". Excluding means xi > Fi." qnd th8s method overall
Actually, distribution of n objects into r groups does not take into consideration of limit of any value.So C(n+r-1,r-1) has many extra values also where some values go out of limit.So by inclusion exclusion I can subtract the cases in which exactly one of them goes out of limit,the add the cases where two of them go out of limit and so on..so xi>Fi actually is this case where xi goes out of its limit
Suppose We have n Sets A1, ..., An. Ai is number of equation answers in which xi > Fi. According to Inclusion-Exclusion Principle number of all equation answers in which we have at least one xi > Fi is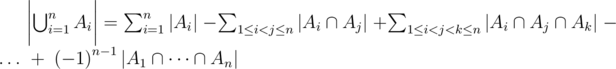 . So the answer to the problem is "Number of ways to pick k flowers from n boxes" without any condition minus the answer that we found using inclusion-exclusion principle.(Complementary Principle) By Now we know the theory. To calculate all these numbers we use bitmasks for all 2n ways. For each mask if bit i is set, We mean that Ai is included in our current subset. With this iteration and knowing how to calculate a big C(n,r) we can compute the final answer easily. Here is my Code.7227622
. So the answer to the problem is "Number of ways to pick k flowers from n boxes" without any condition minus the answer that we found using inclusion-exclusion principle.(Complementary Principle) By Now we know the theory. To calculate all these numbers we use bitmasks for all 2n ways. For each mask if bit i is set, We mean that Ai is included in our current subset. With this iteration and knowing how to calculate a big C(n,r) we can compute the final answer easily. Here is my Code.7227622
I don't know , But I removed the case and it halved the time ~~~~~ if (countFact(n, p) > countFact(k, p) + countFact(n-k, p)) return 0; ~~~~~
in your code , but still AC. Is the test case weak or no need for the check?
This was a pre-written code which was complete for all "mod" cases and other combinatorics and I changed the way it calculates C(n,r) to pass the time limit for this problem. Yes, Deleting it here changes nothing :)
thankyou, i was able to understand it very well
@Amir.bh As you say, "The number of solutions to x1 + x2 + ... + xn = k is C(n + k - 1, n - 1)"
Can you provide some link so that I can learn the theorem for this law at details. Or can you prove this. Please.
sifat_15, [Stars and Bars](https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics))
In the solution of Problem E, the link of "lucas's theorem" is broken.
How would one apply Inclusion-Exclusion on E?
My question too..
http://codeforces.com/blog/entry/13181#comment-179450
I am not able to understand the following observation in Div 2 4th problem : A substring made of the string will be a "good" palindrome if their starting and ending characters are same.
How by only making sure that first and the last character of the substring to be same we are ensuring that substring will be palindrome ??
After merging, the string must alternate between a's and b's. If start with a and end with b, clearly not a palindrome. Otherwise, starts with a and ends with a, must be palindrome in middle (ex: aba, ababa, abababa, etc.)
Oh boy, I completely missed the question. I did not see this restriction that only a's and b's can be there in the input !!!!!
Same here ....Did the same mistake...I was solving for general case and was trying modification of manacher algorithm
Added more explanation to editorial. Ask if still not clear.
My submission got Skipped. I don't know why. Please help... Thanks in advance... My solution: http://codeforces.com/contest/451/submission/7219719
First problem is , you are using while(cin>>n>>m). You should take input just once. See others solution.
Also problem B can be solved with complexity O(n) 7221532
If it helps, I solved "451B — Sort the Array" in O(n). First, find the first i, such that a[i] < a[i-1]. If there is no i (i==n after the for loop), then the array is already sorted. If there is an i that accomplish that condition, find the first j (from i), such that a[j] > a[j-1]. reverse that segment "reverse(a+i-1, a+j)". Then just check if the sequence is sorted or not. I think the worst case is O(3*n) 7234545
yes, this is a good solution. :)
looking at your solution i was reminded of the 300-pointer from TCO Round 2C (a similar problem to B).
Can anyone explain solution for E with inclusion-exclusion principle as detailed as possible? Both Russian and English explanations are acceptable.
Russian: Если шариков каждого цвета неограничено, то s шариков можно выбрать C(s+n-1,n-1) способами.
Теперь посчитаем ответ:
ans=(кол-во способов выбрать s шариков, где шариков каждого цвета может быть сколько угодно) — (кол-во способов выбрать s шариков, где хотя бы для одного цвета, количество шариков >f[i] для всех i) + (кол-во способов выбрать s шариков, где хотя бы для двух цветов, количество шариков для первого >f[i] и для второго >f[j] соответственно для всех i,j) — (по трем) +... +((-1)^n)(по n шарикам)
Чтобы посчитать слагаемые, кроме первого, посчитаем C(s-( сумма(f[i]) по выбранным) +n-1,n-1). Так как n<20, слагаемых 2^20.
Can anyone translate this to English
По-английски фром харт: If count of balls of every color is unlimited then S balls we can choose C(s+n-1,n-1) ways.
And now, let's calculate answer:
answer = (count ways of choose S balls under the stipulation that count of balls of every color is unlimited )
- (count ways of choose S balls under the stipulation that exist at least one color such that we take balls of this color more than f[i] ) + (count ways of choose S balls under the stipulation that exist at least two colors such that we take balls of that colors more than f[i] for 1st color and more than f[j] for 2sd color) - (... at least 3 colors ... ) + ... + (-1)^n * (... at least n colors ... )
To count summand, except 1st, count C(s-( sum(f[i]) of chose colors) +n-1,n-1). Since n<20 then count of summand not more than 2^20.
Can someone write a more detailed explanation of solution to 451E - Devu and Flowers?
first look at: http://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
then A(i1,i2,...,ik) is eaqual to number of different choose when flowers of ij < f[ij] for all j in (1 to k);
the answer is eaqual to ( all — sigma(A(i)) + sigma(A(i,j)) — sigma(A(i,j,k)) + ... );
then look at this :D : 7235306
I have implemented the solution for problem C according to the given editorial but I'm getting WA on test 4.Please can someone help me know what's actually wrong as I am unable to find the bug.Any help will be appreciated.Thank You. http://codeforces.com/contest/451/submission/7234615
Using double may cause errors, it's inappropriate to simply using ">=", "==" to compare a double with an integer
Here's a way to visualise how the inclusion-exclusion principle works.
From the number of all possible ways we subtract the [number of ways where restriction 1 is violated], [-'- restriction 2 is violated -'-], [-'- restriction 3 -'-], ... , [-'- restriction i -'-].
For simplicity, denote the above as bitfields. So: all zeros mean that no restrictions apply, and all 1s mean that all restrictions are violated. So we subtract from N(0000...00) the counts N(1000...00), N(0100...00), N(0010...00), ... , N(0000...01).
But the set where the first and the second restrictions are violated, namely 1100...00, is a subset of both 1000...00 and 0100...00, so by the above subtraction we have subtracted these elements twice from the original set (that also contained it). So it makes sense that we should add them once to make up for that and get things to zero out at this level.
So, onto the above, we add: + N(1100...00) + N(1010...00) + N(0110...00) + ... the rest of these.
Now when it comes to 1110...00, we have subtracted it three times and added it four times (these four times include the three terms added just above plus the original set that contains everything, that we are subtracting from). So we subtract all these items with 3 bits set to make up for it once again.
So far so good, but now the counting gets trickier, so we go straight to the general case. When we reach level W, focus on some item Ww on this level (designated by a certain bit pattern) and look up at all the sets on higher levels that include it (and to which we have already assigned the coefficients +1 and -1 [yes we can say that, because this is the Inductive Step]). This basically means ignoring all the bits that are zeros in Ww as well as the corresponding fields in all the other sets, and if they had a 1 in those fields, they temporarily fade from view. What we're looking at now is a miniature version of a full graph of bitfields (suppose Ww has H bits set to 1), that has 00...0 (H times) at the top and 11...1 (H times) on the bottom, which is Ww. On each level of this smaller graph, all the items have either been subtracted once or added once, in a pattern that alternates with level. Except we don't know the coefficient of Ww yet, this is what we're trying to find out. We want the sum to equal to zero, because, again, we wish to keep excluding all these non-conforming (to all the restrictions) items from the total. Now, if H is even, this smaller graph is symmetric around its horizontal midline, and it's clear that the coefficient of Ww should be -1. Otherwise, if H is odd, then we remember that the counts of elements on the levels of this graph are rows of Pascal's triangle, and each row of Pascal's triangle is the convolution of the previous row with [1 1]. So, if we for the moment picture the distribution of elements over levels as the sum of two identical distributions offset by one, striped alternatingly by [+1 -1], for example
then it's clear that the last coefficient must be +1 to get the sum to be zero (slide the second row and everything will cancel). Therefore, by induction, we know all the coefficients and QED.
If the Pascal's triangle detour seems out of the blue, we can avoid it by directly constructing the sequence of these graphs by adding another bit, which makes two copies of all the vertices, and since the vertices are assigned to levels based on their number of 1 bits, the two copies of the graph are offset by one level relatively to each other when they make up the next graph in the sequence.
Here's a well written note I just finished reading, about Moebius Inversion, which is a generalisation of the idea: http://people.sju.edu//moebinv.pdf
A part of it talks exactly about the above concept, from a different perspective, in fact several. It establishes that the Moebius inversion matrix mu (i.e. the pattern of +-1 coefficients above) of a product of posets (similar to DAGs) P and Q is something like the Kronecker product (I'm thinking of
kronin Matlab) of matrices mu_P and mu_Q. Then it applies this n times to the poset corresponding to just one bit in the above post, i.e. {0, 1}, and gets the alternating +-1 coefficients.Slightly harder version of E: CEOI 2004 Sweets.
Oh,no, I want to solve 4th problem, and I implement the code as the solution. But Why did I got TLE? If I use scanf here,I got TLE,7242064 but I changed it to string,then I got AC.[submission:7242047]How could that be possible?
7242047 this is AC code
strlen is the culprit, It is O(n), not O(1). Don't use this in the loop.
O(n) solution for 451B - Sort the Array
7219814
PraveenDhinwa: Nice editorials and implementations :)
problem 451c- i can't understand this input- 3 1 1 1
I mean, if 1 game had already been played, how can 1st team have already won 1 more game than 2nd team while 2nd team is ahead of 3rd team by 1 game??
will anyone explain please??
Read this comment: 179432
Again, completely incomprehensible editorial. :)
Can you please point out particular section you are having difficulty with?
Can you please explain why the AC output is "yes" for Sample input: 1 9 5 2 1
in problem No.C??
In problem E, I didn't understand the following statement given in the editorial: Now we can find x power s in (1 - x) power - n easily. It is (n+s-1)Cs.
How can a function with negative power have a non zero coefficient for x power s?