I am trying to solve this problem but could not able to solve it. www.codechef.com/problems/LCMSUM
After searching a lot on the web i find this.
summation of (LCM[i,n]) for all i belongs to [1,n] = (((summation of ETF(d)) + 1)*n)/2.
where ETF() euler totient function . and d belongs to set of diviors of n.
Can anybody explain the logic behind it or how does it work. I am unable to find any explanation or details about it. So, can anyone help me.










Now let's group i with the same gcd:
Notice, that when $g > 1$
so
That plus considering g = 1 case will give the required formula.
@alexey.shchepin
Thank you so much for explaining this. I am really glad to know about this prove thank you so much. Can this problem has any other solution.
so complicated..
@alexey.shchepin
Hey! I did not understand the second line of your proof i.e "Now let's group i with the same gcd".
Can you please explain?
Instead of summing directly for i from 1 to n, first find the sum for i when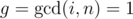 , then for g = 2, and so on. E.g. if n = 12, then we sum in the following order:
, then for g = 2, and so on. E.g. if n = 12, then we sum in the following order:
I was trying to solve it using the "Divisor Sum" formula of Euler Phi. But this looks different. Or maybe it is the same, I just didn't understand it yet. I will go back and think more.
Edit 1: What does "g \ n" means. All g such that it divides n?
Edit 2: [gcd(i,g) = 1] — is this a boolean function? If codition is satisfied [x = 3] is 1 else 0? It's taking more time to undestand the notions than undestanding the solution :|
Edit 3: Finally got it. You reused variables which made thing confusing. Using new variables like j=i/g and x=n/g would have made things easier to understand. Anyways, awesome work! :D
Sorry for that, you guessed right: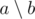 means "a divides b", brackets are Iverson brackets. The notation is from Concrete Mathematics.
means "a divides b", brackets are Iverson brackets. The notation is from Concrete Mathematics.
While the solution based on this math formula may be fast/easy to implement, during the competition I solved it using purely algorithmic solution and I thought it'd be nice to share it for the people disliking too mathy solutions, like myself. My approach is as follows:
Initially using Sieve of Eratosthenes we store all prime numbers in the interval [1; 1,000,000] to allow faster factorization later.
The solution is based on the famous two pointer technique. We keep an active interval with two pointers — left and right, denoting the boundaries of the currently active interval. For start left=right=1. At each iteration we try to increase the right boundary, and if the interval becomes invalid (the LCM isn't equal to the multiplication of all numbers) we start increasing the left boundary until the interval is valid again. It can easily be seen that such solution would have the longest interval as an active one at some point and also moving the pointers takes O(N) in total.
However we need to efficiently add/remove numbers and keep track whether out LCM-property is fulfilled. For the LCM property to be fulfilled, simply all numbers in the set should be pairwise coprime. So each time a number is added, I find all prime numbers that exist in its factorization and for each of them I increase a counter that keeps the amount of numbers in the set that have this prime number as a factor. Obviously if at some point some counter is more than 1, then the set is invalid, that is there are some two numbers that are not coprime. And if all counters are 0 or 1, then the set is valid. This allows adding/removing numbers in O(sqrt Max_Num).
Combining the two things described above we get a solution in O(N * sqrt Max_Num), which is good enough to pass under the given constraints. Mine passed in 7.84ms in CodeChef.
Here is my code if someone is interested, and feel free to ask me if you didn't understand something from my solution.
P.S.
Sorry for being a little bit off-topic and not answering the original question about the mathy solution, but I believe some people may find this solution to be easier to come up with.
@Enchom i think you perhaps misunderstood the problem. problem code is LCMSUM not SUBLCM. but that ok.
I myself was not able to come up with a solution which make use of DP or either two pointers approach but i have formed a O(nlog(n)) solution which could have been passed the test data using one optimisation that i was not able to think during the contest. But after the contest i got AC with the same that is tedious and make use of binary seach and sliding window concept. If you are interested here is my code link .
Not sure what you mean, the code I linked to is the one I submitted to SUBLCM, the problem you link to in your original post?
Edit: I see you've fixed the link now, even though I can't seem to open the new one.
Finally managed to understand the solution. Explained it here: https://forthright48.com/2015/08/spoj-lcmsum-lcm-sum.html.
good explanation....!!
Great explanation!!!
∑lcm(n,i) = ∑ (n*i)/(gcd(i,n)) = n * ∑ i/(gcd(i,n))
Consider the term ∑ i/(gcd(i,n)) , for any divisor “d” of n, there exists ”i” such that gcd(i , n)=d, so i=d*something. Now, ∑ i/(gcd(i,n)) = ∑ (somthing*d)/d = ∑ something .
Since, gcd(something,n/d)=1,what we are looking for is, = ∑ coprime of ( n/d ). So iterate through all divisor “d” of n, and find this term and sum all results.
2nd part: ∑ coprime of (x) = (x* phi(x))/2 .
Proof: let “a” be a coprime of x. than gcd(a,x)=1. So gcd(a-x,x)=1.(if a divides b and c, than a also divides (b+c) and (b-c) ). So if “a ” is a coprime of x, than “x-a” is also a coprime. Each pair of coprime contribute (x+ (x-a)) = x to the sum. There are total (phi(x))/2 pair of coprime (note: no. of coprime is always even except 1 and 2). So total sum = (x*phi(x))/2