489A - SwapSort
All you need is to swap the current minimum with the i-th element each time. You can do it with the code like:
for (int i = 0; i < n; i++)
{
int j = i;
for (int t = i; t < n; t++)
if (a[j] > a[t])
j = t;
if (i != j)
answer.push_back(make_pair(i, j));
swap(a[i], a[j]);
}
This solution makes at most n-1 swap operation. Also if (i != j) is not necessary.
489B - BerSU Ball
There are about 100500 ways to solve the problem. You can find maximal matching in a bipartite graph boys-girls, write dynamic programming or just use greedy approach.
Let's sort boys and girls by skill. If boy with lowest skill can be matched, it is good idea to match him. It can't reduce answer size. Use girl with lowest skill to match. So you can use code like:
sort(boys.begin(), boys.end());
sort(girls.begin(), girls.end());
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (abs(boys[i] - girls[j]) <= 1)
{
girls[j] = 1000;
result++;
break;
}489C - Given Length and Sum of Digits...
There is a greedy approach to solve the problem. Just try first digit from lower values to higher (in subtask to minimize number) and check if it is possible to construct a tail in such a way that it satisfies rule about length/sum. You can use a function `can(m,s)' that answers if it is possible to construct a sequence of length m with the sum of digits s:
bool can(int m, int s)
{
return s >= 0 && s <= 9 * m;
}
Using the function can(m,s) you can easily pick up answer digit-by-digit. For the first part of problem (to minimize number) this part of code is:
int sum = s;
for (int i = 0; i < m; i++)
for (int d = 0; d < 10; d++)
if ((i > 0 || d > 0 || (m == 1 && d == 0)) && can(m - i - 1, sum - d))
{
minn += char('0' + d);
sum -= d;
break;
}
The equation (i > 0 || d > 0 || (m == 1 && d == 0)) is needed to be careful with leading zeroes.
489D - Unbearable Controversy of Being
Let's iterate through all combinations of a and c just two simple nested loops in O(n2) and find all candidates for b and d inside. To find candidates you can go through all neighbors of a and check that they are neighbors of c. Among all the candidates you should choose two junctions as b and d. So just use https://en.wikipedia.org/wiki/Combination All you need is to add to the answer  , where r is the number of candidates (common neighbors of a and c). The code is:
, where r is the number of candidates (common neighbors of a and c). The code is:
for (int a = 0; a < n; a++)
for (int c = 0; c < n; c++)
if (a != c)
{
int r = 0;
for (int b = 0; b < nxt[a].size(); b++)
if (nxt[a][b] != a && nxt[a][b] != c && g[nxt[a][b]][c])
r++;
result += r * (r - 1) / 2;
}
It is easy to see that the total complexity is O(nm), because of sum of number of neighbors over all junctions is exactly m.
P.S. I'll be grateful if some of you will write editorial of E and F in comments because of now I should leave Codeforces and will return back some hours later. Thank you for participation!











very nice problem in this round,very thanks MikeMirzayanov :)
I needed just 2 minutes for problem D T_T
My solution 8732482 of D.
I use this fact:
If
Ais adjacency matrix andB = A ^ kthen number of different path whitslength = kfromutov= B[u][v]Also i speed up matrix multiplication using fact that we have only m
'1'in matrix.That's pretty much the same I think
Problem D:
Start a small ( just 2 steps ) dfs ( or bfs ) from each graph vertex, count the number of ways to get from current vertex in some other ( let it be cnt[v] ). Then add
cnt[v] * ( cnt[v] - 1 ) / 2to the answer.My Code
Hello! Very nice approach to the problem. I just couldn't get why do you used the combination! Could you explain me that?
Suppose that we get 3 ways of reaching a vertex X now suppose they are:
A -> B -> X A -> C -> X A -> D -> X
now we need to select 2 of the given 3 paths to make a rhombus ie BC or CD or BD, so total rhombus are nC2 , where n is the number of ways of reaching the vertex in one dfs (after 2 steps)
your "used" array is useless.
For problem D:
I went through all the nodes, and for each node, I choose 2 of its neighbors (I try them all), then add to the sum the common neighbors of those 2.
My Code
Similar approach but used a different implementation.code
Here is my editorial for F:
The state of the board can be stored with three variables: The row we're on, the number of columns which have no 1s in them (call it x), and the number of columns with exactly one 1 in them (call it y). We then have the following options, depending on these counts.
For each row, we need to select two indexes to be 1s, the rest need to be zero. Here are the possible ways to do that. If x > 1, there are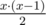 ways to choose two columns to insert a 1. This decreases x by two and increments y by 2.
ways to choose two columns to insert a 1. This decreases x by two and increments y by 2.
If x ≥ 1 and y ≥ 1, then there are x·y ways to choose the two columns.
If y > 1, then there are ways to choose the two columns to insert a 1. This decreases y by 2.
ways to choose the two columns to insert a 1. This decreases y by 2.
Combining all of these methods together yields the right answer.
youll need to save memory for row number when using dp
During the contest I came up with a similar idea.(didn't submit...), but stuck with stupid thoughts T_T. So the dp should be something like: dp[line][x][y], which means at current line, after I have put 1's, when I now have x columns containing no 1s and y columns containing one 1, how many possible ways can I place 1's as the matrix from line 1 to current line.
And current state will have effect to dp[line+1][x-2][y+2](I choose 2 no-1-columns), dp[line+1][x][y-2](I choose 2 one-1-columns), dp[line+1][x-1][y](I choose 1 one-1-column and 1 no-1-columns). This is describled by arknave.
The result will be dp[n][0][0] since each column should contain exactly 2 ones.
And for each line, we have to calculate all the status derived from last line, so the time complexity should be O(m*n^2).
Here is my solution. 8740822
Oops, O(n^3)
You can reduce that to O(n^2). My O(n^3) got TLE.
Notice that you don't actually need to maintain a parameter for row. You can calculate what row you are at from number of zero-columns and one-columns you have. If you have 3 zero columns and 2 one columns, that means you have to put 3*2 + 1*2 = 8 one's inside the matrix still. That means, 8/2=4 rows have not been determined yet.
Just remove row from memoization and solution becomes O(n^2). My Submission: 8737649
You can also use a queue or sth else to maintain the actual states for the O(n^3) dp. It will reduce the complexity of your dp to n^2.
Didn't realize that. Thanks a lot :)
why haven't we taken the case of selecting both from the no 1s or both from both one 1s in the case of x>=1 and y>=1 thus adding (x*(x-1))/2 and (y*(y-1))/2 to x.y?
EDIT:Got it
wait for F solution
I use dp to solve pF. You can count the number of ones in each column, than you could use [500][500] to dp. If the first represent how many columns have 0 one, and the second means 1 one. Than you can use dp.
And the answer is all columns have 2 ones (ans=[0][0])
Thank you, bro, it's a good solution!
e....it looks like you made a small mistake: [i][j] += [i — 2][j + 2] * C(i, 2); [i][j] += ... [i][j] += ...
means we choose two in i columns who have 0 one to two columns who have 1 one.
And this is the same:
It have many ways to get the answer, you can choose your way.
Well, thank you~
Solution for E: The idea is to binary search for the best ratio. So now, this problem reduces to checking if a certain ratio is possible. Let K be the optimal ratio.
First, add a dummy node at x=0, and between every pair of nodes with x_i < x_j, add an edge with cost sqrt(|x_j-x_i-L|) — R * b_j. We will now show that if the shortest path from x=0 to x_n is negative, then we have (sum of frustrations) — R * (sum of picturesqueness) < 0, so (sum of frustrations) / (sum of picturesquness) < R. We know that K <= (sum of frustrations) / (sum of picturesquness), thus, we get that R > K. On the other hand, if the shortest path is positive, then this implies R < K. Thus, we can binary search for the optimal K. Once we've found K, we can then just do the standard dp while keeping prev pointers to reconstruct the path.
I have a question. If (sum of frustrations) — R * (sum of picturesqueness) < 0 then R > (sum of frustrations) / (sum of picturesquness) > K leads to R > K. But if (sum of frustrations) — R * (sum of picturesqueness) > 0 then R < (sum of frustrations) / (sum of picturesquness), i cant find out why this leads to R < K.
EDIT : I have found out why that leads to R < K. Tks for a nice solution :)
Why it leads to R<K ? Would you please explain .
Let f be the sum of frustrations, p be the sum of picturesqueness. When the shortest path is positive => all path from x1 to xn is positive => f — R*p is positive for all f and all p => with EVERY pair of f and p we have f/p > R => K > R.
Thanks for the explanation .
(a1+a2)/(b1+b2) = R
(a1+a2) -R*(b1+b2) = 0 // if and only if R is the answer
What is the meaning of shortest path in this question?
Since we did a binary search, we can only check down to a certain finitely small resolution of the ratio. How can we be sure that there does not exist another answer which actually has a better ratio, but due to our resolution in binary search, was ignored? Plus, I think since the problem deals with real number, there should be a limit on the resolution of the answer. For example, if the optimal ratio is 1.000001, the solution which yields 1.000002 should also be correct. Or maybe in this case, we can; with the given constraints; prove that two solutions must differ by at least some value.
Some other similar problems: http://poj.org/problem?id=2728 http://poj.org/problem?id=3621
.
Good tutorial
Nice Idea. We could somehow deal with fractions as one value whose optimal can be found out easily with dynamic programming (shortest paths).
I have one doubt in its implementation. How do we decide the needed precision for binary search in such problems ? Or do we just keep it very low, but not low enough for Time Limit to be issue.
Excellent idea. Thanks for sharing!
Editorial for D: What i did is a DFS but checking whether a edge is visted or not if edge is not visted. if(edge is visted ) i do nothing else what i do is dfs(current parent) and before entering the dfs i upadte all paths from let say parent to child(current) Link for Solution: Solution
My solution for D is to iterate through every possible start and stop point (a and d) and then calculate the number of b and c respectively. I made a mistake that in the O(n^2) loop, i used the memset() function to memset an O(n) array. Expected to be O(n^3) but still AC. Could anyone explain? The link to my code is below http://codeforces.com/contest/489/submission/8728972
It's a nice Round ! That helps me get more than 300 ratings ! Thanks for MikeMirzayanov !
Life of real man according to MikeMirzayanov
- live in O(nm), be a man
Would someone mind to share the DP solution for problem B? :)
Can anybody tell me why this code is giving TLE ??
most O(n^3) solution for C got TLE because of strict time limit. The mod function take more time than + — * and /.
You can reduce it to O(n^2) by the fact that remain_row=2*(no_of_zero)+(no_of_one)
Can someone explain why the complexity is O(mn) and not O(n^2 m) At least the j++ in the second loop does get executed n^2 times. So how can we give the argument that the second loop is only executed m times?
this only enumerate all adjacent vertices of 'a' there are degree(a) 'b's
O(n*n*Sigma_a(deg(a))) =O(n*m)
I think O(n*n + Signma_a(deg(a)) ) == O(n*n + m) at max.. Correct me if i am wrong. How will O(n*n*Sigma_a(deg(a))) make O(n*m)
Each node is accessed only n times and whenever a node is accessed loop runs for deg(a) times.
consider outer loop to be loop of reference starting points for 'damn rhombi'.
consider 1st inner loop to be ending point. Now 1st inner loop runs for O(n).
Now, 2nd inner loop that finds candidates run for O(deg(a)).
Hence, total complexity would be O(sum_over_all_a(n*deg(a))).
this would be O(2*n*m)=O(n*m).
If you want to implement this solution you would need to make both adjacency matrix as well as adjacency list.
It is not clear to me why the total complexity for D is O(mn). Could somebody explain it to me?
Can someone give the DP solution for Problem C? Thanks :D
http://codeforces.com/contest/489/submission/8730920
http://codeforces.com/contest/489/submission/19787251
I don't see why my adjacency matrix approach didn't fit in the time limit for problem D, it should takes O(n) for each new path and O(nm) in total for solving the problem, which is the same as the editorial's solution.
Could any help please? Thanks in advance, any suggestions would be appreciated. =D
in problem B.
how to apply maximum flow.
Can somebody explain BerSU Ball's recursive DP solution?
https://codeforces.com/contest/489/submission/53830291
Can u plz explain your code... thanks
Just in case there is a harder variation of 489A — SwapSort, there is an O(n * log(n)) method (that kinda resembles using a linked list to me): 53566076
What is the complexity of D solution? I'm pretty confused it. My opinion is (n^2 +m). Is that right?
Can problem B be done Online ?
My code for C fails on case 4 not sure why... Any help would be much appreciated
try test case m=3 and s=10
https://codeforces.com/contest/489/submission/176150923
This is my solution to the D problem,
Any idea why this fails
I did it in
O(nm + n^2)=O(nm)