First of all, sorry for the late editorial. I was too exhausted and immediately went to bed after the round finished, and didn't write the editorial.
There are many pictures in this editorial, to cover up my poor English skills! If you have detected any errors or have questions, feel free to ask questions by comments. Unfortunately, the authors only know English, so we can't answer you if you write comments in Russian.
500A - New Year Transportation
Let's assume that I am in the cell i (1 ≤ i ≤ n). If i ≤ n - 1, I have two choices: to stay at cell i, or to go to cell (i + ai). If i = t, we are at the target cell, so I should print "YES" and terminate. If i > t, I cannot go to cell t because I can't use the portal backwards, so one should print "NO" and terminate. Otherwise, I must go to cell (i + ai).
Using this method, I visit each cell at most once, and there are n cells, so the problem can be solved in linear time.
What is test 13?
There are 9 pretests in this problem. There are no test where n = t holds in pretests. Many people didn't handle this case, and got hacked or got Wrong Answer on test 13.
- Time: O(n)
- Memory: O(n) (maybe O(1))
- Implementation: 9335683
500B - New Year Permutation
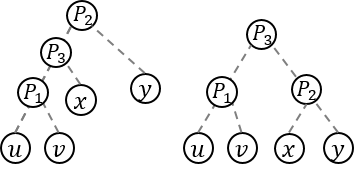
It seems that many contestants were confused by the statement, so let me clarify it first. Given a permutation p1, p2, ..., pn and a n × n-sized binary matrix A, the problem asks us to find the lexicographically minimum permutation which can be achieved by swapping two distinct elements pi and pj where the condition Ai, j = 1 holds. (From the statement, permutation A is prettier than permutation B if and only if A is lexicographically less than B.)
Let's think matrix A as an adjacency matrix of a undirected unweighted graph.
If two vertices i and j are in the same component (in other words, connected by some edges), the values of pi and pj can be swapped, using a method similar to bubble sort. Look at the picture below for easy understanding.

Because all the two distinct vertices in the same component can be swapped, the vertices in the same component can be sorted. In conclusion, we can solve the problem by the following procedure.
- Find all the connected components.
- For each component, sort the elements in the component.
- Print the resulting permutation.
The size limit is quite small, so one can use any algorithm (DFS/BFS/..) for as many times as you want.
- Time: O(n2) — because of the graph traversal. O(n3) is okay because of small constraints.
- Memory: O(n2)
- Implementation: 9335689 (.o.)
What is test 15? There are too many wrong answers in this case.
Actually, I made the pretests very weak in order to make many hacks. As mentioned in the Hack me! post by kostka, just swapping the elements greedily could pass the pretests easily. There were 14 pretests, and I made test 15 an counter-example of such algorithm in order to reduce judging time, and it seems that most of the wrong submissions failed in this test case :D
500C - New Year Book Reading
In order to calculate the minimum possible lifted weight, we should find the initial stack first. Let's find the positions one by one.
- First, let's decide the position of book b1. After day 1, book b1 will be on the top of the stack, regardless of the order of the initial stack. Therefore, in order to minimize the lifted weight during day 1, book b1 must be on the top of the initial stack. (so actually, in day 1, Jaehyun won't lift any book)
- Next, let's decide the position of book b2. (assume that b1 ≠ b2 for simplicity) Currently, b1 is on the top of the stack, and it cannot be changed because of the procedure. Therefore, in order to minimize the lifted weight during day 2, book b2 must be immediately below book b1.
Considering this, we can find the optimal strategy to create the initial stack: Scan b1, b2, ..., bm step by step. Let's assume that I am handling bi now. If bi has appeared before (formally, if 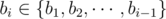 ), erase bi from the sequence. Otherwise, leave bi. The resulting sequence will be the optimal stack.
), erase bi from the sequence. Otherwise, leave bi. The resulting sequence will be the optimal stack.
You should note that it is not necessary for Jaehyun to read all the books during 2015, which means the size of the resulting sequence may be smaller than n. The books which doesn't appear in the resulting sequence must be in the bottom of the initial stack (obviously). However, this problem doesn't require us to print the initial stack, so it turned out not to be important.
In conclusion, finding the initial stack takes O(n + m) time.
After finding the initial stack, we can simulate the procedure given in the statement naively. It will take O(nm) time.
500D - New Year Santa Network
The problem asks us to calculate the value of
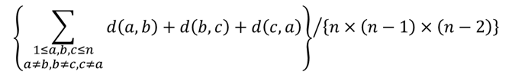
Let's write it down..
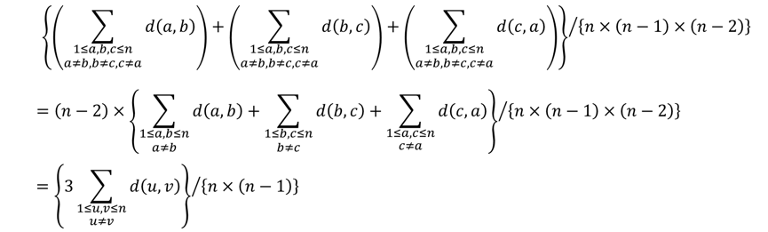
So, we need to calculate the value of 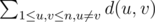 . I'll denote the sum as S. How should we calculate this?
. I'll denote the sum as S. How should we calculate this?
For simplicity, I'll set node 1 as the root of the tree. Let's focus on an edge e, connecting two vertices u and p. See the picture below.
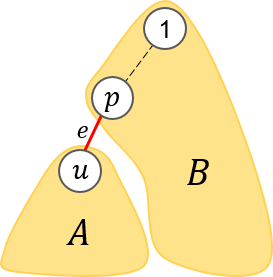
Set A is a set of vertices in the subtree of vertex u, and set B is a set of vertices which is not in the subtree of vertex u. So, 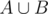 is the set of vertices in the tree, and
is the set of vertices in the tree, and  is empty.
is empty.
For all pairs of two vertices (x, y) where the condition 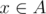 and
and 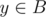 holds, the shortest path between x and y contains edge e. There are size(A) × size(B) such pairs. So, edge e increases the sum S by 2 × le × size(A) × size(B). (because d(x, y) and d(y, x) both contributes to S)
holds, the shortest path between x and y contains edge e. There are size(A) × size(B) such pairs. So, edge e increases the sum S by 2 × le × size(A) × size(B). (because d(x, y) and d(y, x) both contributes to S)
size(A) (the size of the subtree whose root is u) can be calculated by dynamic programming in trees, which is well known. size(B) equals to N - size(A).
So, for each edge e, we can pre-calculate how many times does this edge contributes to the total sum. Let's define t(e) = size(A) × size(B), (A and B is mentioned above). If the length of a certain road e decreases by d, S will decrease by t(e) × d. So we can answer each query.
- Time: O(n) (pre-calculation) + O(q) (query)
- Memory: O(n) (O(n + q) is okay too)
- Implementation: 9335695 (.o.)
Something about precision error
Because of the tight constraints, the total sum of d(a, b) + d(b, c) + d(c, a) (it is equal to S × (n - 2)) can be so large that it can't be saved in long long(64-bit integer) type. Some contestants didn't handle this and got WA.
However, there are some contestants who saved this value divided by n × (n - 1) × (n - 2) in double type. double has 52 bits to store exact value, so it isn't enough. But because we allow 10 - 6 precision error, it seems to have been got accepted.
What if we allowed the length of the road could become 0? Then the precision error gets much more bigger, and the solution prints something that is far from the expected value (for example, negative value). ainu7 discovered this effect and suggested to apply this, but we didn't because it was hard to fix the statement..
Why does the road length decreases? It doesn't matter even if increases.
It's because of the weird legend. It is hard to explain, "People repairs a certain road per year, and its length may be increased or decreased." fluently for me..
500E - New Year Domino
From the statement, it is clear that, when domino i falls to the right, it makes domino j also fall if and only if pi < pj ≤ pi + li.
For each domino i, let's calculate the rightmost position of the fallen dominoes R[i] when we initially pushed domino i. From the definition, 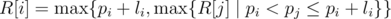 . This can be calculated by using a segment tree or using a stack, in decreasing order of i (from right to left). After that, we define U[i] as the smallest j where R[i] < pj holds. (In other words, the smallest j where domino j is not affected by pushing domino i)
. This can be calculated by using a segment tree or using a stack, in decreasing order of i (from right to left). After that, we define U[i] as the smallest j where R[i] < pj holds. (In other words, the smallest j where domino j is not affected by pushing domino i)
Now, the problem becomes: Calculate P[U[xi]] - R[xi] + P[U[U[xi]]] - R[U[xi]] + ..., until U[xi] ≤ yi. Because i < U[i], this task can be solved by precalculating 'jumps' of 2something times, using the method described in here. You must read the "Another easy solution in <O(N logN, O(logN)>" part..
Formally, let's define Un + 1[k] = U[Un[k]] and Sn + 1[k] = Sn[k] + (P[Un + 1[k]] - R[Un[k]]). So, Sn[k] means the sum of domino length extensions when we initially push domino i and we prolonged the length exactly n times. U2i + 1[k] = U2i[U2i[k]], and S2i + 1[k] = S2i[k] + S2i[U2i[k]] holds. (If you don't understand this part, I suggest you to read the article linked above)
- Time :
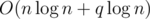 or
or 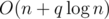 .
. - Memory :

- Implementation: 9335698 (.o.)
- We would like to know whether there is a linear offline solution or not.
500F - New Year Shopping
The i-th item is available during [ti, ti + p - 1]. In other words, at time T, item i is available if and only if ti ≤ T ≤ ti + p - 1. This can be re-written as (ti ≤ T and T - p + 1 ≤ ti), which is T - p + 1 ≤ ti ≤ T. With this observation, we can transform the item's purchasable range into a dot, and the candidate's visit time into a range: From now on, item i is only available at time ti. and each candidate pair (aj, bj) means that I can visit the store during [aj - p + 1, aj], and my budget is bj dollars at that visit. This transformation makes the problem easier to solve.
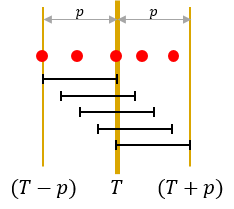
Each red circled point denotes an item which is sold at that time, and each black interval denotes a candidate. Let's only consider the intervals which passes time T. All the intervals' length is exactly p, so the left bound of the interval is (T - p) and the right bound of the interval is (T + p).
For each interval, we'd like to solve the 0/1 knapsack algorithm with the items that the interval contains. How can we do that effectively? There is an important fact that I've described above: all the interval passes time T. Therefore, the interval [aj - p + 1, aj] can be split into two intervals: [aj - p + 1, T - 1] and [T, aj].
So, let's solve the 0/1 knapsack problem for all intervals [x, T - 1] (T - p ≤ x ≤ T - 1) and [T, y] (T ≤ y ≤ T + p). Because one of the endpoints is fixed, one can run a standard dynamic programming algorithm. Therefore, the time needed in precalculation is O(S × W), where S is the number of items where the condition 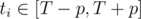 holds.
holds.
Let's define h(I, b), as the maximum happiness I can obtain by buying the items where the condition 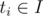 holds, using at most b dollars. For each candidate (aj, bj), we have to calculate h([aj - p + 1, aj], bj), which is equal to max0 ≤ k ≤ b{h([aj - p + 1, T - 1], k) + h([T, aj], b - k)}. So it takes O(bj) = O(W) time to solve each query.
holds, using at most b dollars. For each candidate (aj, bj), we have to calculate h([aj - p + 1, aj], bj), which is equal to max0 ≤ k ≤ b{h([aj - p + 1, T - 1], k) + h([T, aj], b - k)}. So it takes O(bj) = O(W) time to solve each query.
The only question left is: How should we choose the value of T? We have two facts. (1) The length of intervals is exactly p. (2) The algorithm covers intervals which passes time T. Therefore, to cover all the intervals given in the input, we should let T be p, 2p, 3p, 4p, ... (of course, one by one), and run the algorithm described above.
Then, what is the total time complexity? Think of intervals [0, 2p], [p, 3p], [2p, 4p], [3p, 5p], .... For each point, there will be at most two intervals which contains the point. Therefore, each item is reflected in the pre-calculation at most twice, so the time needed to precalculate is O(n × W). The time needed to solve each query is O(bj), and the answer of the query is calculated at most once. Therefore, the time needed to answer all the queries is O(q × W).
- Time : O((n + q) × W).
- Memory : O(n × W)
- Implementations: 9335699 (ainta), 9335703 (ainu7) , 9335710 (.o., using a different approach), 9335709 (.o., using a divide and conquer approach)
Divide and Conquer approach
Let's assume that t1 ≤ t2 ≤ ... ≤ tn. We can easily know that at time T, the indexes of all the available items forms a segment [l, r]. (in other words, item l, item l + 1, ..., item r - 1, item r is available) We can use this fact to solve all the queries. Let's assume that item lj, item lj + 1, ..., item rj - 1, item rj is available at time aj.
Define a function solve(L, R). This function calculates the answer for queries where the condition L ≤ lj ≤ rj ≤ R holds. Let's assume that L < R holds. (In the case L ≥ R, the answer can be calculated easily) Let 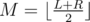 . Call solve(L, M) and solve(M + 1, R). After that, the queries needed to be calculated, satisfies the condition lj ≤ M < rj, which means all the intervals(queries) passes item M. Now, to calculate the answer for such queries, we can use the method described at the dynamic programming approach.
. Call solve(L, M) and solve(M + 1, R). After that, the queries needed to be calculated, satisfies the condition lj ≤ M < rj, which means all the intervals(queries) passes item M. Now, to calculate the answer for such queries, we can use the method described at the dynamic programming approach.
The time complexity is 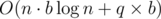 , because
, because 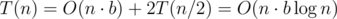 and the answer of the queries can be calculated in O(bj) per query.
and the answer of the queries can be calculated in O(bj) per query.
- Time :
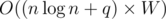 .
. - Memory : O(n × W)
- Implementation: 9335709
Unfortunately, this approach is offline, because of the memory. Is there any available online approach using divide and conquer?
Blocking the divide and conquer solution
I tried my best to block divide and conquer solutions, but failed. It seems that many participants solved the problem with divide and conquer approach. My approach takes 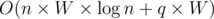 time, and it gets accepted in 546ms.
time, and it gets accepted in 546ms.
500G - New Year Running
Before starting the editorial, I'd like to give a big applause to Marcin_smu, who solved the problem for the first time!
Warning: The editorial is very long and has many mistakes. There are lots of lots of mistakes.. Keep calm, and please tell me by comments, if you discovered any errors.
This problem can be solved by an online algorithm. Let's focus on a single query (u, v, x, y). This means that JH runs between u and v, and JY runs between x and y.
Just like when we solve many problems with undirected trees, let vertex 1 be the root of the tree. Also, we will assume that they won't stop after when they meet, but they will continue running, in order to explain easily.
Some definitions:
- Path (a, b): the shortest path between vertex a and vertex b.
- d(a, b): the length of Path (a, b).
- LCA(a, b): the lowest common ancestor of vertex a and vertex b.
Finding the common path of two paths
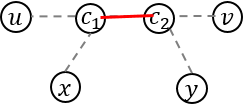
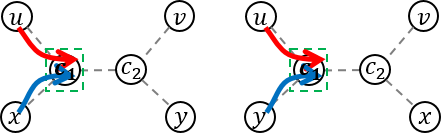
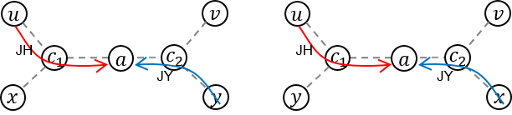
If there is no common vertex between Path (u, v) and Path (x, y), the answer will be obviously - 1. So, let's find the common vertices first. Because the path between two vertices is always unique, the common vertices also form a path. So, I'll denote the path of the common vertices as Path (c1, c2). c1 and c2 may be equal to: u, v, x, y, and even each other.
The possible endpoints are P1 = LCA(u, v), P2 = LCA(x, y), P3 = LCA(u, x), P4 = LCA(u, y), P5 = LCA(v, x), and P6 = LCA(v, y). Figure out by drawing some examples. (some of you might think it's obvious :D)
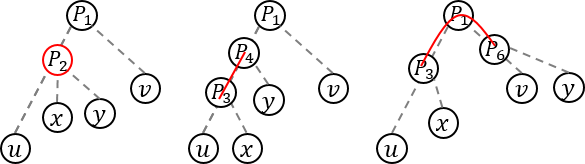
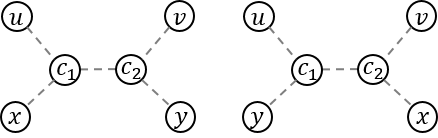
See the pictures above, and make your own criteria to check whether the two paths intersects :D
A small hint. Let's assume that we already know, that a vertex a lies on path (x, y). If a lies on path (u, v), a is a common vertex of two paths. What if a is guaranteed to be an end point of the common path?
Additional definitions
- Let's denote JH's running course is:
 . Then, there are two possible courses for JY:
. Then, there are two possible courses for JY:  and
and  ).
).
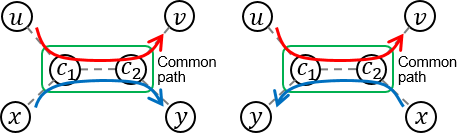
- fJH : the time needed to run the course
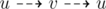 .
. - fJY : the time needed to run the course
 .
. - t1 : the first time when JH passes vertex c1, moving towards c2.
- t2 : the first time when JH passes vertex c2, moving towards c1.
- t3 : the first time when JY passes vertex c1, moving towards c2.
- t4 : the first time when JY passes vertex c2, moving towards c1.
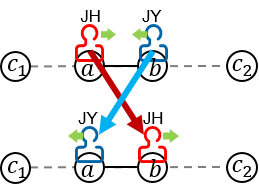
Case 1) When JH and JY meets while moving in the same direction
Obviously, they must meet at vertex c1 or vertex c2 for the first time. Without loss of generality, let's assume that they meet at vertex c1. In this case, both of them is moving towards vertex c2. (You can use the method similarly for c2)
Let's assume that JH and JY meets at time T. Because the movements of both runners are periodic, T must satisfy the conditions below:
Among possible T-s, we have to calculate the smallest value. How should we do? From the first condition, we can let T = fJH × p + t1, where p is a non-negative integer. With this, we can write the second condition as: 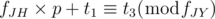 . In conclusion, we have to find the smallest p which satisfies the condition
. In conclusion, we have to find the smallest p which satisfies the condition
Using the Extended Euclidean algorithm is enough to calculate the minimum p. With p, we can easily calculate the minimum T, which is the first time they meet. If there is no such p, they doesn't meet forever, so the answer is - 1.
Case 2) When JH and JY meets while moving in the opposite direction
In this case, they will meet at a vertex lying on Path (c1, c2). Without loss of generality, let's assume that JH is going from c1 to c2, and JY is going from c2 to c1.
I'll assume that JH and JY meets at time T.
[1] Let's see how JH moves: For all non-negative integer p,
- At time fJH × p + t1, he is at vertex c1, moving towards c2.
- At time fJH × p + t1 + d(c1, c2), he is at vertex c2.
Therefore, when fJH × p + t1 ≤ (current time) ≤ fJH × p + t1 + d(c1, c2), JH is on Path (c1, c2). So, T must satisfy the condition:
- fJH × p + t1 ≤ T ≤ fJH × p + t1 + d(c1, c2)
[2] Let's see how JY moves: Similar to JH, for all non-negative integer q,
- At time fJY × q + t4, he is at vertex c2, moving towards c1.
- At time fJY × q + t4 + d(c2, c1), he is at vertex c1.
Therefore, when fJY × q + t4 ≤ (current time) ≤ fJY × q + t4 + d(c2, c1), JY is on Path (c2, c1). So, T must satisfy the condition:
- fJY × q + t4 ≤ T ≤ fJY × q + t4 + d(c1, c2)
[3] These two conditions are not enough, because in this case, they can meet on an edge, but they cannot meet on a vertex.
We'd like to know when do they meet on a vertex, like the picture below.
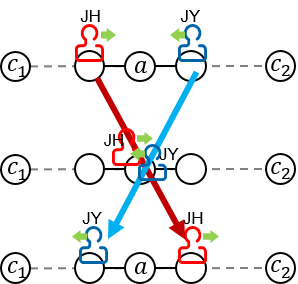
As you see from the picture above, in this case, the condition d(c1, a) + d(a, c2) = d(c1, c2) holds. If this picture was taken at time s, this condition can be written as:
2s - (fJH × p + fJY × q) - (t1 + t4) = d(c1, c2)
s = {d(c1, c2) + (fJH × p + fJY × q) + (t1 + t4)} / 2
Because JH and JY both travel their path back and forth, fJH and fJY are all even. Therefore, in order to make s an integer, d(c1, c2) + t1 + t4 must be even. This can be written as
[4] Merging [1], [2] and [3], we can conclude that if these two conditions holds,
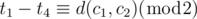
- max{fJH × p + t1, fJY × q + t4} ≤ min{fJH × p + t1 + d(c1, c2), fJY × p + t4 + d(c1, c2)}
JH and JY meets on a certain vertex lying on path (c1, c2). The first condition can be easily checked, so let's focus on the second condition. The second condition holds if and only if:
- fJY × q + t4 - t1 - d ≤ fJH × p ≤ fJY × q + t4 - t1 + d
You can check this by changing "fJH × p" to the lower bound and the upper bound of the inequality. Therefore, the problem is to find the smallest p which satisfies the condition above.
Let's define a function g(M, D, L, R), where M, D, L, R are all non-negative integers. The function returns the smallest non-negative integer m which satisfies 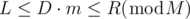 . This function can be implemented as follows.
. This function can be implemented as follows.
- If L = 0, g(M, D, L, R) = 0. (because L = 0 ≤ D·0)
- If
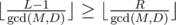 , it is "obvious" that there is no solution.
, it is "obvious" that there is no solution. - If 2D > M, g(M, D, L, R) = g(M, M - D, M - R, M - L).
- If there exists an non-negative integer m which satisfies L ≤ D·m ≤ R (without modular condition), g(M, D, L, R) = m. Obviously, we should take the smallest m.
- Otherwise, there exists an integer m which satisfies D·m < L ≤ R < D·(m + 1). We should use this fact..
If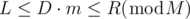 holds, there exists an non-negative integer k which satisfies L + Mk ≤ D·m ≤ R + Mk. Let's write down..
holds, there exists an non-negative integer k which satisfies L + Mk ≤ D·m ≤ R + Mk. Let's write down.. D·m - R ≤ M·k ≤ D·m - L Because
- R ≤ M·k - D·m ≤ - L
L ≤ D·m - M·k ≤ R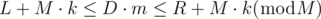 , we can write the inequality as
, we can write the inequality as 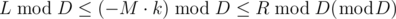
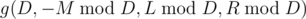 . We can easily calculate the smallest p using k.
. We can easily calculate the smallest p using k.
Then, what is the time complexity of calculating g(M, D, L, R)? Because 2D ≤ M (the 2D > M case is handled during step 3), the problem size becomes half, so it can be executed in 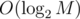 .
.
Conclusion
For each query, we have to consider both Case 1) and Case 2), with all possible directions. Both cases can be handled in 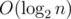 , so the time complexity per query is
, so the time complexity per query is 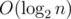 , and it has really huge constant.
, and it has really huge constant.
- Time:
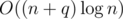
- Memory:

- Implementation: 9330235



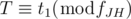
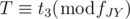
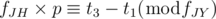
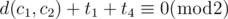








great editorial,with pictorial representation :D
Clicking on the implementation links lead to blog of GoodBye 2014 and saying that you are not allowed to view the requested page.
Edit : Apparently it leads to the last page you opened on CF.
Edit 2 : It works now.
Ye, I've got the same issue.
me too :(
I fixed this error. Is it now okay?
Yes, thanks a lot for the editorial. It's really awesome and the implementations are also cleanly coded.
How do we intuitively understand that the weights of the books don't matter in C?
I did it intuitively but I find it very difficult to explain. Here is the key observation that led me to the solution: "If book A is read before book B, then weight[A] will be added to the total weight lifted while retrieving book B. So to retrieve any book X, we need to lift weight equivalent to the total weights of the books that were read after the last time X was read."
Hope this helps!
Actually, it is not necessary to think about optimal book stack in 500C - New Year Book Reading. It is easy to come up with an idea that iff we have an optimal book stack, then each we will have to lift up only books appeared before current one but after it's previous appearance in b array (or the beginning of b array, if no prev. appearance found), and that's the optimal strategy. So, the thing is: we iterate through b array, each time we take a book, we just add to result every book met before this one, but after current book's previous appearance in b array. This works, too.
Good strategy! It seems that the time complexity of this problem can be reduced to O(n + m) using your solution. Am I right?
On each day j, we want to know the sum of the weights of the books that have been read since the last time bj was read, ignoring duplicates. This could be done using a Binary Indexed Tree in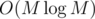 , by storing wi at index d if book i was last read on day d. Overall it would be
, by storing wi at index d if book i was last read on day d. Overall it would be 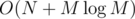 . I am not sure how to make it O(N + M).
. I am not sure how to make it O(N + M).
To prove that this idea is correct, you still need to think about the optimal book stack. The idea that we cannot avoid lifting certain books places a lower bound on the answer. To show that the lower bound is attainable, the most straightforward way is to construct the ordering that achieves it.
i used in C another strategy:
i didn't calculate initial stack. let's go from end of the array. for b[i] find previous b[j] == b[i](j = 1...i — 1), that means that after j-th move b[j] on top. than add to ans weights of different elements from j + 1 to i — 1. if there are no j, just add to ans weights of differenet elements from 1 to i — 1
When I try to view the solution 9332153(for E), I am told that "You are not allowed to view the requested page".
There should alway be a MAX pretest for problems with precision like D.
on question D i used long double does long double have more bits to save the integer value?
That's codeforces format, pretests do not have to cover everything. Thinking about precision and overflow issues was, I think, a significant part of this problem.
P.S. I didn't notice the long long overflow and got WA22.
On this submission: http://codeforces.com/contest/500/submission/9347870
I think I have an overflow problem because of the negative values on the test case I'm getting WA.
However, I can't see why the example solution linked on the editorial (http://codeforces.com/contest/500/submission/9335695) works, since he gets the same value (I assume) and multiplies it by the same amount (3.0/(n*(n-1)).
Could anyone please help me understand what's wrong with my solution?
n × (n - 1) is very big, but you used
intto calculate the variablefactor. You should calculatefactorlike this:3.0 / ((long long)n * (n-1))I thought there would be no problem since I'm assigning the result to a double.
Didn't think about the overflow that happens before the cast. Thanks for the help, got AC now! (HNY actually :D)
Best editorial I've ever read.
I solved F that way: In scanline we need to write 0-1 knapsack for queue. That can be done calculating dp like queue from two stacks. 9328164
Could you explain a bit more on your $$$a[0], a[1], b[0], b[1]$$$ in your submission? It was really long time ago but I was so curious about this approach as this "scanline" thing can be come up obviously but the DP part of adding and deleting elements seems to be so hard. Thanks <3
please can anyone explain to me why we use combinations in such problems like problem D ?!
Awesome editorial, thank you!
Task E is very simple to solve by self-expanding segment tree. Here is my implementation : 9333521
Can you explain what makes your implementation so fast? My submission(9336904) seems to be much much slower than yours..
I don't know. Maybe my super-heuristics in assign and get void gave a performance boost :D
What is that self-expanding segment tree? Can you please provide me with some link?
I made a blog post asking for help on E: http://codeforces.com/blog/entry/15565 , cause I thought it would be too big for a comment here.
Could anyone please help me find what's wrong with my solutions?
(Tried using a stack on one as mentioned in the editorial, but I get TLE. Then tried using a segtree, but I'm getting WA on an early test case and can't spot what's wrong :'( )
can anyone explain 3rd step in Problem D's solution (the math equations)?
In the (bigger) curly brackets, there are:
sum of d(a, b) for all 1 ≤ a, b ≤ n, a ≠ b
sum of d(b, c) for all 1 ≤ b, c ≤ n, b ≠ c
sum of d(c, a) for all 1 ≤ c, a ≤ n, c ≠ a
We can change each to: sum of d(u, v) for all 1 ≤ u, v ≤ n, u ≠ v (see the part I used bold)
So we have 3(d(u, v) for all 1 ≤ u, v ≤ n, u ≠ v)
Out of the (bigger) curly brackets, (n - 2) / (n - 2) = 1, so we can omit it
Now we have 3(d(u, v) for all 1 ≤ u, v ≤ n, u ≠ v) / (n × (n - 1))
Thanks for reply but I don't understand how (n-2) came in the third step
When we get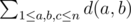 we can see that c doesn't do anything to d(a,b), so this sum will be the same thing no matter what value c gets. Ok?
we can see that c doesn't do anything to d(a,b), so this sum will be the same thing no matter what value c gets. Ok?
So, how many different c are there for the same pair (a,b)?
Since c != a and c != b, there are n-2 different values.
Thus, for each possible c, there will be a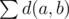 , and since there are n-2 possible c's:
, and since there are n-2 possible c's:
And since the three sums are equal, we get 3 * that.
=)
Three sums are actually the same. The only difference is names of the variables.
My Pascal code for problem B: 9333946
Even with editoral & without forces of time, this problem took me 30 minutes to get AC.
This is the best solution that I have ever read :)
cgy4ever's is close: after sorting the queries, it seems to take O(n + qα(n)): 9316327
9346692 is o(n+q) + sorting
upper_boundisGreat editorial, great pictures! What software are you using to draw these ?
I used PowerPoint 2013 to make pictures for the problems and the editorial.
For D,
Lets say we have edge u - v, with countU as the number of nodes left of u including u, and countV similarly for nodes right to v including v.
Now this edge u - v will not be included if all 3 nodes were from left or right of it.
So, contribution of this edge = (P(n, 3) - P(countU, 3) - P(countV, 3)) * 2 * w.
I solved E using Dynamic Segment Tree and offline processing. A little bit memory efficiency is needed here! :D Here is the code
http://hzwer.com/5935.html
Can you explain why the time of question b is O(n2)? the implementation is O(n3) because when you are reading input you have two loop and in second loop you use "merge_group(i, j)" that need O(n) time.
merge_group(i, j) takes amortized O(alpha(n)) time where alpha(n) is inverse Ackermann function. Since Inverse Ackermann function grows really slowly It is mostly taken to be constant. http://en.wikipedia.org/wiki/Disjoint-set_data_structure
merge_group(i, j)is not really O(n) because he used Path Compression for Union Find Disjoint Sets in the implementation. You can read the details here.Hope it helps!
Edit: sorry, I didn't reload before post (so I didn't know that SameerGulati had answered)
Actually, disjoint set data structure is not required. You can just use any graph traversal algorithm like DFS or BFS, then you will archive complexity O(n2). My code's time complexity is O(n2α(n)).
In problem B why swapping is not correct?For example if we do 10cycles and check if it's possible to make array prettier better to do it.Of course it will give TLE,but idea idea is correct right?
Take a look at these comments.
I'm the author of problem G. Thanks to .o. for the great editorial!
How did you come up with it? o.O
I think the hardest part of this problem is Case 2) When JH and JY meets while moving in the opposite direction. And it is related to this problem. Before I made problem G, I already solve that problem. So I could come up with this idea.
Someone help me problem:500B - New Year Permutation. I dunno know why it's wrong!?? My submission:9366210 Thanks a lot!!
You use the same variable to iterate in two overlapping loops.
Can someone please help me with my solution for 500E-New Year Domino. My submission:14303491
I'm interested in divide and conquer solution of problem F. Could anyone explain or at least give an outline of such a solution?
Just wrote the explanation of the divide and conquer solution briefly. Please answer me if you have any questions.
I have a general question regarding problems similar to 500C which use greedy algorithms. How does one correctly guess a greedy solution to such kind of problems? It could happen that one has a greedy solution but it is wrong.
I was initially thinking about a solution on the lines of how a particular frequently a book is read.Higher the frequency,closer the book should be to the top of the stack.But realized it was incorrect.
Any particular technique regarding how to think about such problems?
The key is to always try to make a proof that it works (or doesn't work). I don't mean a very formal one (unless you're very good at it :D), but just from the top of your head.
When going for a greedy solution, I usually do something like:
1) Try to prove it's correct. If I succeed -> code it
2) Try to find a counterexample. If after some thought I can't find any and I strongly believe that it works, then I code it. (If I don't feel very strong about it, I put the problem aside and come back to it later :P).
Now, on how to 'prove' it, try to build a reasoning starting from the base cases. Think about what "must be true" or "is certainly false". And when doing the other way around (trying to find a counterexample to show it doesn't work) try to build an example from the 'failing' condition.
To illustrate, my thought proccess on C was something like:
The base case is when you have one book. It's on top, nothing to lift. Cool.
Now if you have two books. On the first day the minimum you have to lift is still 0, if it's on top, there can't be anything better.
On the second day, regardless of what book you are going to read you MUST have read the first book on the other day. So, suppose it's a different book, you need to lift the previous one (there's no other way around it). There's really no reason to not have that first book on top in the first day (costing 0), since on the second day (and the days after) you are gonna need to lift it anyway (it's gonna be on top on the second day, regardless of where it was before).
On third day, same stuff happens for the third book (still assuming different books). So it seems like the correct thing to do is only lift what you have read before.
Now, the only cases left are when you are going to read a book that you have previously read. What happens then? You need to lift every book that you've read since you last read it. Since the book must be there, because there's really no other way, then there's no other way around it too. GOT IT.
Think about it to simplify a little bit ("So whenever you need to read a book, you lift everything since you've last read it and put it on top, no other way around it, got it") -> Double check to see if every assumption is true for realz or if I'm just being stupid (sometimes that's the case :'( ) -> Code it!
I started trying to prove more what I was thinking when I realized how much time I wasted coding wrong greedy solutions that I wasn't sure about :P You get better every time you try to do that.
Hope that helps!
I really enjoyed this problemset, I honestly learned something new from each problem I did not know how to do. Thank you :)
I am having doubts in New Year Permutation though it is an easy problem still I am unable to understand can any help me ?? Thank you in advance
I think that this picture can help; (for example: K, L belong to one component and A, B, C, H to another) http://support.sas.com/documentation/cdl/en/ornoaug/65289/HTML/default/images/concomp1.png
You have to find all components in graph, given matrix is actually adj matrix ('1' means that edge exist between position i and position j, and '0' that it doesn't exist). Finding components are easy with graph traversal (BFS, DFS). It's obvious that you can arrange elements in component however you want, and of course you will sort it, because it is your task. After sorting all elements in all components you have to output that array.
Why you're so bad? Hahaha, you should be more explicit in the statements!