500A — New Year Transportation
In this problem we are given a directed graph, and asked whether a particular vertex is reachable from vertex 1. It is possible to solve this by running a depth-first search starting from vertex 1.
Since every vertex has at most one outgoing edge, it is possible to write the DFS as a simple loop. Some people used this to make very short submissions.
500B — New Year Permutation
Imagine a graph with one vertex for each entry in the permutation, and edges between pairs of swappable entries. It is easy to see that no matter how many swaps we make, no entry can end up in a location that is not in its connected component. We can also show that within any connected component, we can achieve any rearrangement of the entries that we wish.
Since we want to make the lexicographically smallest permutation, we should greedily rearrange the entries within each connected component so that they are in increasing order.
N ≤ 300, so we are not concerned with runtime. One can determine the connected components using a number of standard algorithms (Floyd-Warshall, Union Find, etc.).
500C — New Year Book Reading
Consider an arbitrary day d, on which we must read book b. Let d' be the last day before d on which book b was read (if there is no previous day, let d' = - ∞). Observe that, on day d, we cannot avoid lifting all of the books read on any day between d' and d. If we add up all the weights of these required liftings, we will have a lower bound on the answer.
This lower bound can be computed with two loops, in O(M2) time. We must be sure not to add a book's weight multiple times, if it was read multiple times in the interval (d', d).
If we initially arrange the books in order of the first day on which they are read, we will achieve the described lower bound. So, we have our answer.
500D — New Year Santa Network
By linearity of expectation, E(d(c1, c2) + d(c1, c3) + d(c2, c3)) = E(d(c1, c2)) + E(d(c1, c3)) + E(d(c2, c3)). By symmetry, those three values are all equal. So, we need only compute E(d(c1, c2)). We can multiply it by 3 to find the answer.
Let us imagine that a random selection (c1, c2, c3) is made. We'll define a function f(j), for each edge j, so that f(j) = wj if j is part of the shortest path from c1 to c2, and f(j) = 0 otherwise. Observe that  . Again by linearity, we have
. Again by linearity, we have  .
.
We can write E(f(j)) = wj·P(j), where P(j) is the probability that edge j is included in the path from c1 to c2. If we compute P(j) for all j, we can then compute 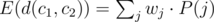 in O(N). Also, we can handle updates in O(1); if wj changes to w'j, we subtract wj·P(j) from the answer, and add w'j·P(j).
in O(N). Also, we can handle updates in O(1); if wj changes to w'j, we subtract wj·P(j) from the answer, and add w'j·P(j).
So, let's figure out P(j) for each j. Any edge j, if removed from the tree, separates the graph into two separate connected components a and b. Edge j will be included in the shortest path from c1 to c2 if and only if one of them is in a, and the other is in b. So, we want the number of ways to select (c1, c2, c3) such that c1 and c2 are on opposite sides of edge j, divided by the total number of ways to select (c1, c2, c3). Let's have |a| and |b| denote the number of vertices in a and b, respectively. Then 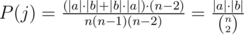 .
.
To figure out |a| and |b| for each j, we can root the tree arbitrarily and compute the depth and subtree size for each vertex in O(N) time. Then for an edge j, if vj is the deeper vertex incident to j, we know one component has size equal to the subtree size of vj. For the other component, we use the fact that |b| = N - |a|.
500E — New Year Domino
When domino i is knocked over, it covers the interval [pi, pi + li]. If we see a query (xj, yj), it is equivalent to the question "If we knock over all dominoes with index 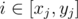 , how much of the interval [pxj, pyj] won't be covered?" We can modify that question a little more, to say that we knock over all dominoes with index i ≥ xj, without changing its answer.
, how much of the interval [pxj, pyj] won't be covered?" We can modify that question a little more, to say that we knock over all dominoes with index i ≥ xj, without changing its answer.
Now, consider knocking over the dominoes from right to left. As soon as we knock over domino i, we will immediately process all of the queries with xj = i, and record their answers. What we need is a data structure that supports two operations: "cover range [pi, pi + li]" (when we knock over a domino) and "compute how much of the range [pxj, pyj] is not covered" (when we wish to answer a query). This can be done using coordinate compression and a segment tree.
It's worth noting there are a lot of other ways to solve this problem. The other tutorial uses a completely different approach. Also, the approach described here may be implemented using different data structures. For example, here is my implementation using BBSTs and a Binary Indexed Tree.
500F — New Year Shopping
We will use the standard dynamic programming approach for 0/1 knapsack. To summarize what it does for us, imagine we are given an ordered list of items (ci, hi). Let F(k, b) be the maximum happiness we can buy, if we consider only the first k items in the list, and have a budget of b. If K is the size of the list, and B is the maximum possible budget, we can compute F(k, b) for all possible k and b in O(KB) time.
Let us sort all of the items by their display time. Suppose that we focus on the queries (aj, bj) with 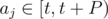 , for some particular t. Let A be a list of the items with display time in (t - P, t], and let B be a list of the items with display time in (t, t + P). Let both lists be sorted in order of display time.
, for some particular t. Let A be a list of the items with display time in (t - P, t], and let B be a list of the items with display time in (t, t + P). Let both lists be sorted in order of display time.
Every query with 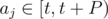 will have available to it some suffix of A, along with some prefix of B. We'll do a knapsack DP on the elements of A, in reverse order, and another on the elements of B, in normal order. Finally, to answer any query (aj, bj) with
will have available to it some suffix of A, along with some prefix of B. We'll do a knapsack DP on the elements of A, in reverse order, and another on the elements of B, in normal order. Finally, to answer any query (aj, bj) with 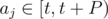 , we can consider all possible ways to split the budget bj between the items in A and the items in B, in linear time. For each possible way to split the budget, we need simply look up one value from each DP table to know the maximum possible happiness.
, we can consider all possible ways to split the budget bj between the items in A and the items in B, in linear time. For each possible way to split the budget, we need simply look up one value from each DP table to know the maximum possible happiness.
If we perform the process above on t = 1, 1 + P, 1 + 2P, 1 + 3P, ... until t exceeds the maximum possible day D, we'll be able to answer all of the queries. Let's think about the runtime of this solution. For each t, the described process takes O(KB) time, where K is the number of items whose display time is in (t - P, t + P). Each object can only appear in up to two of these intervals. So, the overall runtime for all of the knapsack DP's we perform is O(nB). Computing the final answer takes O(B) per query, or O(qB) overall.
500G — New Year Running
Don't know how to solve this yet. Maybe someone who is not gray can provide the solution. :)











In 500E, how exactly can the problem be solved by coordinate compression and segment trees? If we compress the coordinates, isn't it possible that the data integrity is lost? Thanks for the tutorial!
Without coordinate compression, you would use a segment tree in which the leaves correspond to the ranges [1, 2], [2, 3], [3, 4], and so on. The idea with the coordinate compression is to combine leaves whose behavior is always the same. For example, in a test case with only one domino (pi = 1, li = 109), it is not necessary to build a segment tree with 109 different leaves. We can just have one leaf corresponding to the range [1, 109 + 1], because at any time, that range is either fully covered or fully uncovered.
The only way a leaf's behavior can differ from a neighboring leaf's behavior is if there is a domino either ending or beginning between them. This places a manageable bound on the number of leaves we need.
For E -> No need of coordinate compression . You can write a pointer segtree with lazy propogation creating nodes while updating , though you have to do a few optimizations to reduce the memory usage . code -> 11763750 . Time and space complexity is O((N + Q) * LOG(10 ^ 9)).
@rajat1603 You have nice code , but I donot get the flow ? can u please elaborate about the flow of your code , how storing cordinates give you cost ?
Ah, the infamous RDTree returns.
Hello! I have a question reagarding "new year permutation". I have used the following idea. If i have an inversion (i,j), then, by swapping Pi and Pj I obtain a lexicographically smaller permutation, right? So I've found a greedy algorithm: While there are inversions which are allowed to be swapped, I swap them. However, my submission has wrong answer on test 15. Is my logic flawed? If so, then where am I wrong? I haven't been able to come up with a counterexample to my algorithm.
Imagine that the initial permutation is 2 1 3, and we are able to make swaps (1, 3) and (2, 3). The greedy will not make any changes, since neither swap makes the string smaller. However, it is possible to reach the permutation 1 2 3.
I am sorry, I have accidentally voted down your comment and I don't know how to undo it
LOL no problem
thanks, man !!!
Solution for 500A using dfs?
Here is the DFS solution for 500A - New Year Transportation-
Solution: 32035002