519A - A and B and Chess
Author: BekzhanKassenov
This problem asked to determine whose chess position is better.
Solution: Iterate over the board and count scores of both player. Then just output the answer.
Complexity: O(n2), where n is the length of the side of the board (8 here)
Code: 10083191
519B - A and B and Compilation Errors
Author: ADJA
In this problem you were given three arrays. Second array is the same as the first array without one element, third array is the same as second array without first element. You were asked to find deleted elements.
Solution: I'll describe easiest solution for this problem: Let's denote a as sum of all elements of first array, b as sum of all elements of second array and c as sum of all elements of third array. Then answer is a - b and b - c
There are also some other solutions for this problem which use map, xor, etc.
Complexity: O(N)
Code: 10083248
519C - A and B and Team Training
Author: ADJA
In this problem we should split n experienced participants and m newbies into teams.
Solution: Let's denote number teams with 2 experienced partisipants and 1 new participant as type1 and teams with 1 experienced participant and 2 new participants as type2. Let's fix number of teams of type1 and denote it as i. Their amount is not grater than m. Then number of teams of type2 is min(m - 2 * i, n - i). Check all possible i' and update answer.
Complexity: O(N)
Code: 10083265
519D - A and B and Interesting Substrings
Author: ADJA
In this problem you were asked to find number of substrings of given string, such that each substring starts and finishes with one and the same letter and sum of weight of letters of that substring without first and last letter is zero.
Solution: Let's denote sum[i] as sum of weights of first i letters. Create 26 map < longlong, int > 's, 1 for each letter. Suppose we are on position number i and current character's map is m. Then add m[sum[i - 1]] to the answer and add sum[i] to the m.
Complexity: O(NlogN), where N — the length of input string.
Code: 10083293
519E - A and B and Lecture Rooms
Author: BekzhanKassenov
In this problem we have to answer to the following queries on tree: for given pairs of vertices your program should output number of eqidistand vertices from them.
Let's denote:
dist(a, b) as distance between vertices a and b.
LCA(a, b) as lowest common ancestor of vertices a and b.
depth[a] as distance between root of the tree and vertex a.
size[a] as size of subtree of vertex a.
On each picture green nodes are equidistant nodes, blue nodes — nodes from query.
Preprocessing: Read edges of tree and build data structure for LCA (it is more convenient to use binary raise, becase we will use it further for other purposes).
Complexity: O(NlogN)
Queries:
We have to consider several cases for each query:
1) a = b. In that case answer is n.
2) dist(a, b) is odd. Then answer is 0.
3) dist(a, l) = dist(b, l), where l = LCA(a, b).
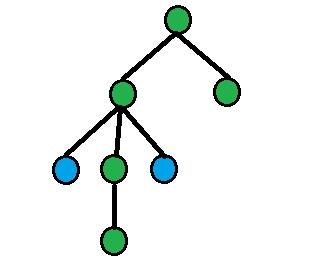
Find children of l, which are ancestors of a and b (let's denote them as aa and bb). Answer will be n - size[aa] - size[bb].
4) All other cases.
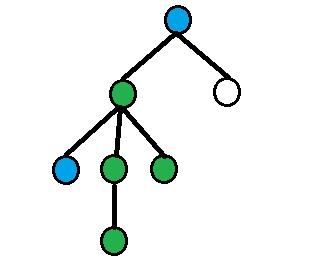

Assume that depth[a] > depth[b]. Then using binary raise find dist(a, b) / 2-th ancestor of a (let's denote it as p1), dist(a, b) / 2 - 1-th ancestor of vertex a (denote it as p2). Answer will be size[p1] - size[p2].
Complexity: O(logN) for each query, O(MlogN) for all queries.
Resulting complexity:: O(MlogN + NlogN)
Code: 10083310











Problem C can be solved in O(1) time. Just 1 line of code! cout<<min(m,min(n,(m+n)/3))<<endl;
Check my solution
Why was the above solution downvoted. It is very good!
People here loves to downvote.
I did the same couldn't figure out the need for dynamic programming in this specific case
Can u explain your solution ?
The secret is here
(m+n)/3 means that you take 1 type and 2 type for 2/3 teams and reverse type for the other 1/3 teams.
And that cuz of the two values n and m is close to each other so there are no precious type.
if n is minimum means that you take 1 type n and 2 of m for all teams
that happens if you m is greater than m by (2*n) which means n is so precious so you must use all of it.
and the same thing for m when n is greater than 2*m by m then m is precious and you must use all of it.
yeah it's good one. I upvoted
Actually I thought it's wrong cuz of downvotes So thanks.
519C — A and B and Team Training my codes got a AC,but do not know why,can somebody prove that?
int main (){ LL a,b; cin >> a >> b; cout << min((a+b)/3, min(a,b)) << endl; return 0; }
Think of creating a matrix with maximum number of rows and 3 columns such that each row should contain at least 1 newbie and 1 experienced player and fill the rest with remaining players. If the number of newbie players is more than 2 times the number of experienced players then the number of experienced players itself is the answer since each team should contain at least one experienced player. Just interchange experienced and newbie in the previous sentence.
If you have enough players, the maximum number of teams that can be formed is floor((m+n)/3). Fill the newbies and experienced players in the grid vertically such that each row satisfies the conditions mentioned in the question.
Thanks. Through your thoughts.I prove that by maths.
The number of teams is x, the newbie is a, the experienced player is b. Each team have a newbie and a experienced player at least. After that, the rest of newbie is (a-x), the rest of experienced player is (b-x). After complete team, the left player is (a-x) + (b-x) — x.
if 0 <= (a-x) + (b-x) — x < 3,then x <= (a+b)/3 < x+1, so x = (a+b)/3. The left player may have newbie and experienced player, so x <= a or x <= b, so x <= min(a,b), so (a+b)/3 <= min(a,b). else if (a-x) + (b-x) — x >= 3, the left player is all newbie or all experienced player. The other is in team. so we get x <= (a+b)/3-1 and x = min(a,b), so x = min(a,b) < (a+b)/3.
Through discuss, if 0 <= (a-x) + (b-x) — x < 3. x = (a+b)/3 <= min(a,b) => x = min((a+b)/3, min(a,b)). else if (a-x) + (b-x) — x >= 3 x = min(a,b) < (a+b)/3 => x = min((a+b)/3, min(a,b)).
so. the number of team x = min((a+b)/3, min(a,b)).
My English is so bad, excuse me.
why (a-x) + (b-x) — x is less than 3 ??
Because while (a-x) + (b-x) — x is less than 3, the left players do not form a team. And (a-x) + (b-x) — x is equal or greater than 3, we can sure that the left player is all newbie or all experienced player.
But How you will handle the case when newbie players are greater than the experienced players but are less than the 2*experienced players and vice versa.
Oh.. The prob. D is map<longlong,int> which I used map<int,int> .. pretest is ok then I failed system test. Sad story. QAQ
same here :(
hello the sum could exceding int 32 bits because in the case a = 100000 b = 100000 ..... z = 100000
n * 100000 = 10^10 > 32 bits int overflow....
Can anybody share some problem links related to the problem E :) . It will be a great help :).
Here is very useful link for LCA algorithm in <nlogn,mlogn> time complexity and there are some problem links also related to that. http://www.topcoder.com/tc?d1=tutorials&d2=lowestCommonAncestor&module=Static#Lowest Common Ancestor (LCA)
Can you upload the pictures some where else. I can't see them :(
B solution is great!
Could anybody explain more problem D? How is that map working? What is stored there?
map<long long, int> m[26]; m[i] stores <sum, num of prefixes ending with char 'i'>
What you do with that map, is store what was the sum for the previous characters. If you sum 6 for an 'a', and then find another 'a' that the sum for previous characters is 6, that means that the sum between the first 'a', and the second 'a' is 0, because they have the same sum range.
I used this approach too, and got an AC despite expecting a TLE. Can you tell me why 10^5 element insertion in a map is passing? I've found it to give a TLE many times. Test cases not strong?
A simple C++ map has O(log(n)) insertion, deletion, and searching operations. With n = 10^5, think that your algorithm is doing just 10^5 * log(10^5) = 10^5 * 17 = 1.700.000 operatios (in average), and you can do aprox. 30.000.000 operations per second in a normal judge (or more), and for this problem you have 2 seconds. So it would never give you TLE.
Sadly I've still encountered problems where 10^5 is a problem. But now I realise, this is CF we're talking of here, and unlike SPOJ, its servers are fast.
I don't think an O(n log n) approach can give you TLE with 1 second in any judge. If you have some examples we can check them.
I can't recall right now, but I'll definitely discuss them with you when I encounter another one. Thanks though! :)
The same code submitted after the contest gave AC but failed on Test 36 during system testing.
Problem: A Failed code: 10066549 Passed code; 10085855
These are the same piece of code. Please look into this.
Can someone share a good tutorial related to the binary raise technique ?
You can find a good tutorial here.
It was good contest & good problems
Could someone explain problem D? What is the map doing there?
The problem asks to compute the number of substrings that begin and end with the same letter, and whose sum of weights equals 0 (ignoring the endpoints).
There is a very simple, correct, and inefficient solution. For each pair (i, j), i < j of occurrences of letter c calculate in O(1) the sum of the inner sub-interval (i + 1, j - 1). Given that this would take O(N^2), we have to discard this solution as N can be as big as 105.
We can do better. Assume we take each occurrence of c in a right-to-left fashion. The occurrence at index j has prefixsum(j) weight. Assume at index i (i < j) we have another occurrence of c. Under what circumstances could S[i... j] be interesting? Well, if prefixsum(i) + weight(c) = prefixsum(j), we have a guarantee that the sum of the elements between i and j is zero-sum.
So, the map is used as a sort of cache that indicates whether we have previously achieved certain prefix sums.
Got it. Thanks.
thx for explanation
My solution for prob.C was binary searching ans with L=1 and R=(m+n)/3
If pair of N experienced participants and M newbies (N,M) can form (L+R)/2 teams then L=mid+1 else R=mid-1;
To check if (N,M) can form x teams I did this: - Assume that (N,M) can form x teams , so we have x1 teams of type1 (XP,XP,NB) and (x-x1) teams of type2 (XP,NB,NB) with x1 in [0..x]. So there will be (x+x1) XP and (2x-x1) NB in total. - Hence the conditions are ((x+x1 <= N) AND (2x-x1) <= M)) OR ((x+x1 <= M) AND (2x-x1) <= N)) with x1 in [0..x]
So the complexity is O(nlogn) i think?
Could problem C be solved using integer linear programming?
Yes. I explained that in this comment http://codeforces.com/blog/entry/16687#comment-215716
E can also be solved using Heavy-Light Decomposition!!!
can you elaborate?
http://blog.anudeep2011.com/heavy-light-decomposition/
The basic approach would be the same......but the subroutines can also be carried out with HLD..........the QTREE2 question on spoj invlolves the similar subroutines.......anudeep2011 has explained it well.....u would want to go through this blog instead of listening to me......THE BLOG IS REALLY FANTASTIC!!!
solution for C :
can anyone explain why this solution works ?
guess this is a solution based on greedy theory.
I doubted this idea during the contest,but now I feel it's quite right to think so.
if(n < m) then it's better to use more m; otherwise it's better to use more n. Am i getting it right?
BTW::another solution is fairly unbelievable the ans is min(min(n,m),(n+m)/3)
But in fact, min(min(n,m),(n+m)/3) is also based on greedy theory. Suppose that n<m, if m>=2*n, we must run out of n, and at the same time, use more m. so we choose 1n2m and the answer become n; if m<2*n, 1<m/n<2 , so we can choose 1n2m for a times and 2n1m for b times, and let a+2b=n and 2a+b=m ,here the answer is a+b=(n+m)/3;
at last, we can combine them together to get the expression:min(n,(n+m)/3), here n=min(n,m)
thanks a lot.understand better now:)
image not visible!!!
Nice problems. I really appreciate them.
Thx for nice problems!
As for problem C, I solved it using linear programming graphically.
Let A = Number of experienced people that will join the contest. B = Number of newbies joining the contest. X = Number of all experienced people. Y = Number of all newbies.
The objective function is to maximize Z = A + B. And the answer will be floor(Z/3).
The constraints are:
A <= 2*B , B <= 2*A , A <= X , B <= YYou can deduce these constraints yourself.If you draw the graph, you can deduce that there are only three cases:
(1) Point (X,Y) is feasible and then it is the answer because it the optimal corner point.
(2) Point (X,Y) is in the upper left of the feasible region, meaning that X < Y / 2. Then the optimal corner point will be (X,2*X).
(3) Point (X,Y) is in the bottom right of the feasible region, meaning that Y < X /2. Then the optimal corner point will be (Y,2*Y).
So you can easily check by conditions which case it is and print Z / 3.
There is another solution which is minimum between (X,Y,(X+Y)/3). Actually it is the same. Because the right case of these three cases will have the minimum value and the other two will be unfeasible solutions, which means that the feasible solution across the three cases is the minimum across the three solutions. And you can check that by drawing.
If you have any question, feel free to ask.
My Submission : 10099801
Thanks for your solution. Can we use binary search for this problem ?
How safe is it to assume that the variables are initialized to zero by default? The code shown here immediately uses timer++ (problem E), as well as ans += and Map[sum[p]]++ in problem D.
depends.. global variables are zero initialized as they are static. whereas local variables dont have any default values
Also value of map automatically initialized to its default value when created (zero for int).
Is it the same for other STL containers (sets, vectors, etc.)?
What are the other implications when you say that global variables are static (if any)?
Solution C: In the solution leftn = n-i is divided by 2. Why?
You group them into 2 of the leftn : 1 of m (or leftm), so you only have leftn/2 of those teams.
In E, what does anc[i][j] store, and how does go_up() work? Are these routines from a standard algorithm?
Another solution for problem C in O(N): If there's more EX than NB, then create a 2EX, 1NB team, else create a 1EX, 2NB team. Stop until it's impossible to create new team.
My solution: 10189473
I have written LCA finding algorithm in <O(N logN, O(logN)> time complexity, but I still get TLE on test 12 on java. Can anybody help me?? here is my solution 10217373
To make it absolutely clear, I mean Problem E.
It seems that the slowest part is following lines:
They make your solution to answer in O(N) because dist can be n - 1 in worst case.
Thanks, you are right! Although, I rewrote the code in C++ and got AC, but I will remake that piece of code to make it even faster. Thank you again!
http://codeforces.com/contest/519/submission/28950258
Can anyone help me find why my solution of problem E is giving TLE in testcase#20???
Use another sparse table or use binary raise technique to add the appropriate subtrees, instead of the for loop you are using.
For problem E, why is the max height is 30?
Div 2 C can be done in a more easily understandable way like 83759343
shortcut for problem C:
ans = min(m, m, (m+n)/3)
Explanation can be found by plotting lines in 2D space