I have often encountered problems(in gym) which reduce to finding C(n,r) % p , where p is not necessarily prime . Also n and r are both large . Essentialy they demand for the use of Lucas and Chinese Remainder Theorem.
For constraints let`s take this problem .
This link does help a lot but I am still confused , especially in the part which asks to use C.R.Theorem . How to apply CRT?
Also what if p is not a square free number ?
Along with explaination , a link to code would be extremely helpful.











Let m and n be coprime,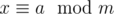 , and
, and 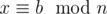 . Then x = ms + a = nt + b where s and t are unknown. Rewrite this as ms - nt = b - a. On the other hand, we can find k and l such that mk + nl = 1, so mk(b - a) + nl(b - a) = b - a. Subtracting the equalities, we get that m(kb - ka - s) + n(lb - la + t) = 0, so kb - ka - s is divisible by n, and mk(b - a) - ms is divisible by mn. So,
. Then x = ms + a = nt + b where s and t are unknown. Rewrite this as ms - nt = b - a. On the other hand, we can find k and l such that mk + nl = 1, so mk(b - a) + nl(b - a) = b - a. Subtracting the equalities, we get that m(kb - ka - s) + n(lb - la + t) = 0, so kb - ka - s is divisible by n, and mk(b - a) - ms is divisible by mn. So, 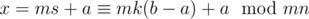 .
.
Okay thanks , i got the calculation part.
But what about my other question ?
what if p is not a square free number ?
You can have a look at this problem's editorial. https://www.hackerrank.com/challenges/ncr
This is implemented according to Granville's generalization of lucas theorem. Follow this link https://math.stackexchange.com/questions/95491/n-choose-k-bmod-m-using-chinese-remainder-theorem