A. You can do exactly what is written in a statement. Only one pitfall in this problem is that room leader may have number of points less than zero.
B. In this problem you may find optimal strategy for a stowaway. Next you may just simulate a game.
Optimal strategy for the stowaway is placing from a conrtoller as far as possible. In the moving minute the stowaway should go into wagon that farther to the controller. In the idle minute stowaway should go into wagon in which the controller enter as later as possible. It is always the first or the last wagon of train.
You may also wrote some dynamic programming solution or a solution fot classic game.
C. Define a trajectory as a line that center of a billiard ball is drawing while it is moving. At begin of moving, the ball chose one from no more than two trajectoties and is moving along of it. Let a number of trajectories is k. Define z as maximal number of billiard balls that can be placed into chessboard without hits (it is answer for problem).
Theorem. z = k.
Proof. Every ball covers at least one trajectory. Two different balls cannot cover one trajectory because then they hit each other. Therefore, z ≤ k.
Now try to arrange k balls that they don't hit each other. Every cell of perimeter of board belongs to exactly one trajectory. Every trajectory covers at least one from border cells. So, there is exists k cells on perimeter of board whick belongs to different trajectories. Into these cells we should put all billiard balls. End of proof.
This theoren gives constructive methode to find k. We may just calculate number of connected component in graph like in a picture below. It can be done by BFS, DFS or disjoint set union in time O(n + m).
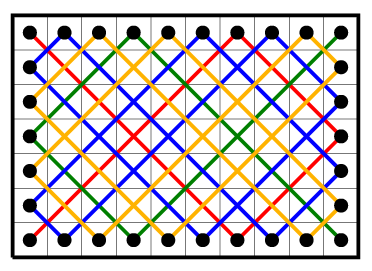
For example, on picture 4 components are present.
In this problem alse some solution by formula exists. z = gcd(n - 1, m - 1) + 1. You may wrote some stupid solution for observe it. But this formula is difficult for prove.
D. You may use some data structire that allows fast insert, search, remove of elements and find a minimum of all elements. There can be used, for example, std::set in C++ or analogicaly container in other languages. In this structure segments of empty hooks can be stored. Minimum element in structure should be a segment into which a current coat can be hanged.
In addition, for every arrived employee you may store place of his coat and segments of empty hooks in the left from this place and in the right from one.
With help of this structures you can in emulate a work of cloakroom. Difficults begins with director's queries. We can fastly insert, delete and find sum in a segment.
emulate a work of cloakroom. Difficults begins with director's queries. We can fastly insert, delete and find sum in a segment.
Online solution. There can be written some balanced or decart tree.
Offline solution. At first, iterate over all queries "in idle" (we will nor answer for director's queries) and store coordinates of all hooks on which ever coat was hanged. Next, squeeze these coordinates and iterate over all queries again. Now we can answer for director's queries by using Fenwick or segment tree.
E. A following sequence of operations swaps two pieces in positions 0 and 1: D1 R1 D1 L1 D1 R1 D1 L1 D1 R1 D1 L1 D1. This sequence can be found on a paper by hands or by usung bidirectional BFS with limitation of allowable moves (it also can be found by ordinary BFS with very limited number of allowable moves). Analogically you can swap any two neighbouring pieces in 13 moves.
Then the solution is trivial and easily fits in the limit of 10000 moves.
B. In this problem you may find optimal strategy for a stowaway. Next you may just simulate a game.
Optimal strategy for the stowaway is placing from a conrtoller as far as possible. In the moving minute the stowaway should go into wagon that farther to the controller. In the idle minute stowaway should go into wagon in which the controller enter as later as possible. It is always the first or the last wagon of train.
You may also wrote some dynamic programming solution or a solution fot classic game.
C. Define a trajectory as a line that center of a billiard ball is drawing while it is moving. At begin of moving, the ball chose one from no more than two trajectoties and is moving along of it. Let a number of trajectories is k. Define z as maximal number of billiard balls that can be placed into chessboard without hits (it is answer for problem).
Theorem. z = k.
Proof. Every ball covers at least one trajectory. Two different balls cannot cover one trajectory because then they hit each other. Therefore, z ≤ k.
Now try to arrange k balls that they don't hit each other. Every cell of perimeter of board belongs to exactly one trajectory. Every trajectory covers at least one from border cells. So, there is exists k cells on perimeter of board whick belongs to different trajectories. Into these cells we should put all billiard balls. End of proof.
This theoren gives constructive methode to find k. We may just calculate number of connected component in graph like in a picture below. It can be done by BFS, DFS or disjoint set union in time O(n + m).

For example, on picture 4 components are present.
In this problem alse some solution by formula exists. z = gcd(n - 1, m - 1) + 1. You may wrote some stupid solution for observe it. But this formula is difficult for prove.
D. You may use some data structire that allows fast insert, search, remove of elements and find a minimum of all elements. There can be used, for example, std::set in C++ or analogicaly container in other languages. In this structure segments of empty hooks can be stored. Minimum element in structure should be a segment into which a current coat can be hanged.
In addition, for every arrived employee you may store place of his coat and segments of empty hooks in the left from this place and in the right from one.
With help of this structures you can in
 emulate a work of cloakroom. Difficults begins with director's queries. We can fastly insert, delete and find sum in a segment.
emulate a work of cloakroom. Difficults begins with director's queries. We can fastly insert, delete and find sum in a segment.Online solution. There can be written some balanced or decart tree.
Offline solution. At first, iterate over all queries "in idle" (we will nor answer for director's queries) and store coordinates of all hooks on which ever coat was hanged. Next, squeeze these coordinates and iterate over all queries again. Now we can answer for director's queries by using Fenwick or segment tree.
E. A following sequence of operations swaps two pieces in positions 0 and 1: D1 R1 D1 L1 D1 R1 D1 L1 D1 R1 D1 L1 D1. This sequence can be found on a paper by hands or by usung bidirectional BFS with limitation of allowable moves (it also can be found by ordinary BFS with very limited number of allowable moves). Analogically you can swap any two neighbouring pieces in 13 moves.
Then the solution is trivial and easily fits in the limit of 10000 moves.











The problems are good
或许是出题人证不出来 :P
In an nxn board , a ball starting from any point on a boundary comes backs to the same point without touching any other ball on the same boundary.
So , it's clear that nxn board is equivalent to nx1 board(for placing the balls) , in which case answer is n.
let a and b be the sides of board,
So if a > b keep on shrinking bxb blocks to bx1 block.
Code:
while( a > 1 && b > 1 ){
if( a > b) a = a - (b - 1);
else b = b - (a - 1);
}
return a + b - 1;
Say , in a x b grid with a > b "the boundary" is the left wall i.e 1st column.
Now trace the path of a ball travelling from from a point at "the boundary" back to some point on "the boundary". You will observe that ball goes and comes back from the same point at (a - b + 1)th column.
Hence , for tracing the paths in order to find conflicting points at "the boundary" we don't require columns farther that (a - b + 1)th column.
This is why we can say a = a - b + 1;
I still do not understand the relationship between this approach and the $$$\gcd(n-1,m-1)+1$$$ approach...
Great Work, absolutely correct! The key point in "reducing the size" was due to the "unchanged positional behaviour" of boundary of (txt) matrix as mentioned above, which is easily provable.
Moreover, a better/general visualization of the problem can be to tessellate the board in R2.