Have a set A. First there are n (n<=40000) number in A. If u and v are in A, LCM(u, v) and GCD(u, v) are in A, too. Give A and a number S, is S in A? Sorry, my English isn't good.
→ Обратите внимание
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3690 |
| 2 | jiangly | 3647 |
| 3 | Benq | 3581 |
| 4 | orzdevinwang | 3570 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | Radewoosh | 3509 |
| 8 | ecnerwala | 3486 |
| 9 | jqdai0815 | 3474 |
| 10 | gyh20 | 3447 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 157 |
| 6 | maroonrk | 155 |
| 7 | -is-this-fft- | 152 |
| 8 | Petr | 146 |
| 8 | orz | 146 |
| 10 | pajenegod | 145 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 17.05.2024 11:38:57 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










What do you mean by S?
Can you please specify the link of the problem?
http://codeforces.com/gym/100442 Problem E here. Multitest, number of tests is given in the first line. Every test is n + array of length n (elements ≤ 1018) + the number you need to check. Output YES or NO.
S is between which numbers?
I think that this problem is:
Given set of intergers. You need to check if given number is equal to LCM of two elements of set.
No, it is not. Imagine n = 3, and initial numbers:
2 3 5
then A = {2, 3, 5, 1, 2 * 3, 3 * 5, 2 * 5, 2 * 3 * 5}.
edit: added 2 * 5, thx misof.
You missed 2*5 in your example.
My intuition says that the answer is yes iff, for each prime p, there is some element x such that p divides x and p divides S an equal number of times.
That's not true for S={6,36} and x=12
Let’s call the set of n numbers given in the input data A0. In mathematical terms, A is the closure of A0 under LCM and GCD.
Now we’ll see that every number in A can be represented as the LCM of some GCDs of some numbers from A0. So we can take the closure of A0 under GCD first and then take the closure of that under LCM to get A. The proof is by induction:
If there is a reasonably small limit on the values of the input numbers,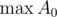 , we can actually compute the closure of A0 under GCD:
, we can actually compute the closure of A0 under GCD:
This takes time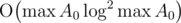 because
because  and because
and because 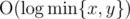 .
.
gcd(x, y)takes timeNow we just need to determine whether S is the LCM of some subset of
gcd_closure. We can do it similarly:This takes time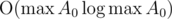 because
because 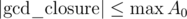 and
and  .
.
lcm(x, y)takes the same time asgcd(x, y)plusSo the whole solution takes time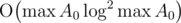 and memory
and memory 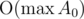 .
.
As we're all throwing random thoughts, my intuition says if the prime factorization of S is product pi ^ ai, and Bi = gcd({ x in A0 : pi^ai divides x}), S is in A iff lcm Bi = S.
I can't formally prove it, but it feels right... Edit: winger proved it in a reply below.
That sounds right, since for each power of a prime dividing S, you are sure to have it in your final number if there is a number with that power as a factor, and you will remove any extraneous primes with the gcd, if it is possible to.
One corner case however is when gcd(A)!=1 and S=1, but that's easily fixed.
Fails on A0 = {20, 25, 250}, S = 100. Clearly , but using this (hypothetical) solution, from S = 22 × 52 we get
, but using this (hypothetical) solution, from S = 22 × 52 we get 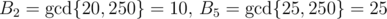 and
and 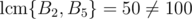 , and so S is rejected.
, and so S is rejected.
4 doesn't divide 250, so B2 is gcd(20)=20.
Oh, you’re right! Sorry.
Here's the proof:
First, let's prove that Bi is the smallest (in terms of divisibility) element of A that is divisible by piai:
Suppose that there is another element of A Bi', that is divisible by piai but not by Bi. Let's also choose Bi' with the smallest formula. The fact that Bi' is not divisible by Bi means that there is prime number power pk that divides Bi but not Bi'. Obviously, p ≠ pi and Bi' is not equal to one of the generators.
In both cases, we found a number that is divisible by piai but not by Bi and with smaller formula than Bi'. Contradiction.
Now, it is easy to show that S is in A iff it is divisible by all Bi, which is equivalent to S = LCM(Bi) (because LCM(Bi) is obviously divisible by S).
Nice! I guess this settles the problem, then. :)