A. You should count a number of vowels for every of three phrases. Next, you should compare this numbers with numbers 5, 7 and 5. If all is matched, answer is YES, otherwise answer is NO.
Author of problem is Ripatti.
B. At first, you can [n / 7] times output string "ROYGBIV" ([] is a rounding down). After than you can output "", "G", "GB", "YGB", "YGBI", "OYGBI" or "OYGBIV" according to remainder of division n by 7. A resulting string will satisfy problem's requirements.
You can also build answer in other way.
Author of problem is Ripatti.
C. If n is even, Marsel wins - he just symmetrically repeats moves of Timur.
Now consider a case of odd n. If Timur cannot move - he is losing automatically. If he can do a move, he always can split one log into few parts that this parts cannot be splitted again. It can be done if we have find minimal t that k ≤ t < m and t|m. Next we split log into parts with length t. Thereafter Timur symmetrically repeats moves of Marsel and wins.
For checking that Timur could move or not, you can iterate over all divisors of m. If there is exists some divisor t that k ≤ t < m, Timar can do a move. Chech of all divisors can be done in 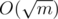 time.
time.
Author of problem is Lepetrandr.
D. It should be solved like a classical problem "count the number of square cells 1x1 lying inside the circle". Firstly, lets find the highest hexagon that lies inside the circle. Then we move to the right and up from this hexagon, and then go down until we find hexagon lying inside the circle. Repeat this process until you reach the rightmost part of the circle.
Thus we can count number of hexagons in each column, answer is sum of this numbers. Total number of operations is O(n).
Few words about implementation. Coordinates of every considered point looks like 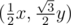 . That's why distance between this points and (0,0) should be calculated using integers only. For example, criteria "point
. That's why distance between this points and (0,0) should be calculated using integers only. For example, criteria "point 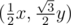 lies inside circle of radius R" looks like x2 + 3y2 ≤ 4R2.
lies inside circle of radius R" looks like x2 + 3y2 ≤ 4R2.
Also you can solve this problem in 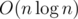 . For every column of hexagons you can find number of hexagons inside circle by using binary search.
. For every column of hexagons you can find number of hexagons inside circle by using binary search.
Author of problem is Ripatti.
E. Firstly, let's calculate the following value:
dp[t][x0][y0][x][y] == true iff scientist from block (x0,y0) can reach block (x,y) in time t, considering toxic coolant.
Secondly, let's consider a graph consisting of 4 parts:
1 - source (one vertex)
2 - first fraction (nxn vertices)
3 - second fraction (nxn vertices)
4 - sink (one vertex)
Each vertex of each fraction is for one block. Build edge from source to each vertex of the first fraction with capability as number of scientists in corresponding block. Build edge from each vertex of the second fraction to sink with capability as number of rescue capsules in corresponding block. Build edge from vertex (x0,y0) of the first fraction to vertex (x,y) of the second fraction iff dp[T][x0][y0][x][y]==true for at least one T. Capability of this edges is infinity.
As one can see, value of maxflow in this graph is answer for the problem.
Complexity of this solution is O(tn4 + kn6), where k is maximum possible number of scientists in each block(in this problem k = 9).
Author of problem is Ripatti.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 18:47:42 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











do
{
randomsolution=randomCalc();
}while(!isValid(randomsolution));
For task B
works as well.