In this problem we can get AC with many solutions:
1) With every new rectangle we will add his area to the result, so for each line x1, y1, x2, y2 we will add to answer (x2 - x1 + 1) * (y2 - y1 + 1)
Time complexity O(n).
2) We can just do all, that is written in the statement: create an array and with each new rectangle we can just increment every element inside rectangle. In the end we can just add all elements inside this array.
Time complexity O(n * x * y)
We can find out a formula for this problem:
for n < 10 answer will be n = n - 1 + 1 = 1 * (n + 1) - 1;
for n < 100 answer will be 2 * (n - 9) + 9 = 2 * n - 9 = 2 * n - 10 - 1 + 2 = 2 * (n + 1) - 11;
for n < 1000 answer will be 3 * (n - 99) + 2 * (99 - 9) + 9 = 3 * n - 99 - 9 = 3 * n - 100 - 10 - 1 + 3 = 3 * (n + 1) - 111;
so for n < 10sz answer will be 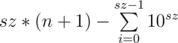 ;
;
Time complexity O(sz), where sz is the length of n.
We also could just try 10 options n < 10, n < 100, ..., n < 109, n = 109 and solve problem for each option.
UPD: Don't use function pow() to find powers of 10, because it doesn't work right sometimes.
Convert m to number system of base w. If all digits of number – 0 or 1, then we can measure the weight of the item with putting weights, that have digits equal to 1, on one pan, and our item on another one.
If this condition isn't satisfied, then we should iterate from lower digit to high and if digit is not equal to 0 or 1, we try to substract w from it and increment higher digit. If it becomes equal to - 1, then we can put weight with number of this digit on the same pan with our item, if it becomes equal to 0, then we don't put weight, in another case we can't measure the weight of our item and answer is 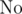 .
.
Time complexity O(logm).
We can look through all pair of points, draw line through each pair and write, that this line includes these 2 points. We can do it with map. If some line includes x points, then in fact we counted, that it has 2 * x * (x - 1) points, because we included each point 2*(x-1) times in this line.
We can create an array and add to him values b[2 * x * (x - 1)] = x, so we can define, how many points is on the line. Then we can iterate through all lanes and for each line with x points we will loose x * (x - 1) * (x - 2) / 6 possible triangles from all possible n * (n - 1) * (n - 2) / 6 triangles. Decide, that at first ans = n * (n - 1) * (n - 2) / 6. So for every line, that includes x points, we will substract x * (x - 1) * (x - 2) / 6 from ans.
Time complexity O(n2 * logn).
UPD: I am sorry, that O(n3 / 6) solutions passed, my solution with O(n3 / 6) didn't pass before the contest, so I decided, that TL 4 sec is good(it was for Java TL).
We can see, that we can reach maximal answer, when brackets will be between two signs * , or between one sign * and the end of expression. For convenience we will add in the begin of expression 1 * , and in the end of expression * 1.
After that we can iterate all possible pairs of signs * and count the expression with putting brackets between two signs * for each pair.
We can use two variables x and y to count the value of expression, in the begin x = 0, y = firstnumber, where firstnumber is first digit of expression, then if next sign is + , then x = y, y = nextnumber, and if next sign is * , then x = x, y = y * nextnumber. The value of expression will be x + y, we can create function, like that, to count expressions inside and outside the brackets.
Time complexity O(|s| * 172).
P.S. Sorry for my bad english, I will try to correct mistakes in the near time.











C was awesome!
I wrote a solution for Problem C in Chinese. http://houjp.com/2015/06/19/codeforces-552c-vanya-and-scales/
I made a different algorithm for B and i like share it with you:
Both are same.
A good point!!!! Whenever is possible make easier only make it !!!
good solution
It's sad to know that O(N^3) passed for problem D for some of my friends while I have been struggling to make an O(N^2 logN) algo. Why 4 sec time limit?? :(
Probably for Java solutions.
for C++ too.
See here: 11655766
UPD: O(N^2 logN) solution here: 11657756
Yeah it is basically because of Java TL, but honestly O(N^3) didn't work for me, I had to re-write an O(N^2 log N) which runs pretty ok-ish
http://codeforces.com/contest/552/submission/11661778
My O(N^3) accepted with 1.6(s) on C++ :)
can you please explain me how the time complexity is O(N^2 logN) ?
Hey, can you see the two nested loops i and j, that accounts for the O(N^2) and inside the j loop there I used map, which takes O(logN) time for insertion.
Hence, complexity is O(N^2 logN).
My Scala O(n^3/6) D took 6 seconds (on my laptop): http://codeforces.com/contest/552/submission/11649585
in D, how did O(n^3) pass for n=2000 I got 2 unsuccessful attempt trying to hack O(n^3) solutions
Codeforces servers run >10^9 operations in 1 second, they are really fast
In case the server run 10^9 in 1 second, there will be no TLE for many problems. So I think maybe the large data is just too lucky --!.
Please check the following two codes for Problem D:
http://codeforces.com/contest/552/submission/11648893
http://codeforces.com/contest/552/submission/11646357
I think both have same time complexity (O(n^3)) but first one got accepted and the other (my solution) got TLE. Why do I get TLE error. Please let me know if I have missed something. Thanks!
As you can see, you have done a lil more constant time computation and also used std::cin and std::cout for I/O while the other person uses much faster scanf and printf.
the main reason of TL is long long.
Woah! I never knew that the data types could affect the running time too. I made the changes and the solution got accepted. Is there an explanation to this? Thanks! :)
The size of different datatypes is different. Generally the trend is, more the number of bits in a datatype, more is the time taken to perform operations on it.
Input/Output — scanf/printf is much faster than cin/cout.
Да ну...
My solution for C was brute force:
if(w = 2 or w = 3)
The answer is always yes
else
Every weights has three cases:
1:on the left pan
2:on the right pan
3:unused
and the order is O(3 ^ x) where w ^ x = m
Mine was exactly same as your solution but i got time limit exeeded. problem in my code was when w = 3. can you explain why the answer is always YES when w = 3? and here is my submission : 11649907
3 base log of 10^9 is ~18.86 ,so the solution becomes 3^18 which gets TLE . but 4 base log of 10^9 is ~14.9 . 3^14.9 is less than 10^8 , so gets ac
you can easily prove it by induction!
Thanks, finally a straightforward advice!
My solution for C was brute force:
if(w == 2 or w == 3)
The answer is always yes
else
Every weights has three cases:
1:on the left pan
2:on the right pan
3:unused
and the order is O(3 ^ x) where w ^ x == m
thnx I did the same saw tle thought It was invalid solution
i tried solving D in contest but got WA.here's my submission...can someone please find a bug in my solution!!
I don't understand the solution for problem C. Specifically the second part -
"if it becomes equal to 0, then we don't put weight, in another case we can't measure the weight of our item and answer is No."
How will it become zero? In base w, no digit will ever exceed w-1, so by subtracting w you can't get zero :/
It can be w if we add one because the previous digit was greater than one.
Oh ok that makes sense! Btw is there any formal proof to this thay why solution does not exist in other cases?
In problem D there was also O(n^2 * maxX) solution. For each pair of points we calculate equation of line y(x). Then for each x coordinate we find y(x) and if it is integer and point (x; y(x)) exists, we decrease number of triangles by 1.
I did the same thing.
D passed in 1.7 seconds and it was
O(N^3)11653540This is not O(n^3), this is O(n^3 / 6)
My solution for Problem C is very simple and it passed: http://codeforces.com/contest/552/submission/11646617
Basically, let's try to solve:
Where each c0, c1, c2 are either -1, 0 or 1.
-1 means we used the weight on right, +1 means we used the weight on left and 0 means we did not use the weight at all.
Now, notice equation 1 and equation 2 -- we are trying to solve the same problem all over again! So let's recurse!
For such a solution to exist (m — c0) must be a multiple of w.
Let's divide both sides by w and recursively solve if we can find such an m-c0 where c0 = -1 or 0 or 1
Here is solution in plain code:
This is also one way of proving that if w = 2 or 3 it always possible since it is guaranteed to find atleast one multiple of 2 and 3 in m-1,m and m+1.
Wow, I loved this solution! Also, you have explained it very well!
Really very nice idea and very nice explanation.
answer for 3 105 should be YES or NO?
Answer is : YES, because : 105 + 3 = 81 + 27.
Wow. Thank you!
in trysolve function,can you explain how recursive relation is working?
Now the remaining c1 + c2*w^1 + c3*w^2 + ... should be equal to (m-c0)/w ,
but you are doing solve(w, (m-c0)/w) isn't this equivalent to c0*w^1 + c1*w^2 + c2*w^3 + ... = (m-c0)
We don't care about actual values of c0, c1 etc. We are just checking if a solution exists. It exists as long as there is a -1 <= c <= 1 such that m-c is divisible by w and (m-c)/w can also be formed by the weights.
That's what I want to ask why (m-c)/w should be again equal c0+ c1*w^1 + c2*w^2 + ...
Please forgive me if it's a dumb question
you call the function trysolve thrice with m,m+1,m-1(possible options of c0) now int that function you first check if the number that you received (ie m or m+1 or m-1) is divisible by w ,if it is you divide it by w and again call the function with the quotient ie (m-c0)/w so now the situaution is c2*w^2+c3*w^3... = (m-c0)/w-c1 ,at each step you'll have three choices for c1,c2...(-1,0,1 ie adding it on left/rigth or not adding it at all) if by subtracting any of these you can make the variable exactly divisible by w you choose that path if thus proceeding you reach the base state m=1 you get the answer as true. hope i made it clear :)
wonderful to solve this problem,easy to understand
Thanks for the great explanation! It should be in the editorial.
A beautiful solution...
Loved your explanation
Nice, really clean solution. Thanks a lot for the explanation :D
In problem B, Why funtion pow() to find powers of 10 doesn't work right sometimes ? ...anyone? in my machine pow() worked well, but when sent to CF judge I receive WA. T_T.
Same problem! I got 5 WA because of this :(
it has to do with pow() returning a double type value. even i got a WA verdict due to this
Use always
ceil(pow(a,b))function.. because pow() returns double and its values is always some what less than anticipated.. eg pow(4,2) will be 15.9999999... so the int will override the value and save it as 15.. using ceil() its ceiling fuction and will solve your problem.. you can also use
(pow(a,b)+0.01)because usually the remainder value is less than 0.01. see 11655937for Problem D,I have subtracted triangles formed from collinear points from total no of triangles but still getting wa. please help .Here is my solution
http://codeforces.com/contest/552/submission/11656405
(For problem B)
why function pow() doesn't work right sometimes?
what should I do in case of finding power ?
Thank you.
The problem with pow is that it returns a floating-point value and you are rounding it to an integer and losing precision. Implement your own exponentiation function using only integer variables and it should be fine.
C can also be solved with this simple approach :-
If m is a power of n then answer is "YES" otherwise check :-
In an array store values of powers of n such that values are less than m .. Also add m and a the power of n just greater than m.. (This is because higher powers of n will not be useful in contributing to the weight on either side !)..
Let elem be the count of elements in the array .. For ex- n=3 m=7, arr={1,3,7,9}; elem=4;
Then simply run a O(2^elem) recursive function to get the values of sum of all 2^elem possible subsets of the array ... If any of the sum (out of 2^elem) repeats then answer is "YES" otherwise "NO"..(It can easily be checked by using a map).
One of my friend Meintoo got it correct during the contest — his iterative solution
here's the link to my solution(after the contest) — recursive solution with comments
Hey I thought of the exactly same approach during contest, but could not come to the conclusion that if ANY of the sum repeats then always answer is "YES" else "NO".
can you please explain that?
Thanks for sharing :)
It is because every sum is a result of different subset so it is guaranteed that at least one element is different in the 2 subsets with same sum ..
And now the catch point — no array for any n can have 2 subsets of equal sum if it has only increasing powers of n .. check it yourself 1,3,9,27 ... no two distinct subsets can b equal ... (holds for any n >=2).
So if we are getting 2 subsets of equal sum then surely the number m is playing its role and is in one of the subset and not in other because its presence in both subsets create the same problem (no array with any n can have 2 subsets of equal sum if it has only increasing powers of n);
So the deed is done .. m is in one of the subset and weights on its side include the numbers in the subset containing m and the other subset constitutes the weight on the other side .. Now in case u worry that same element may be present in both subsets then simply eliminate it(subsets will have same sum, then also) and m can't be in both subsets as stated above .
Hope I explained clearly :)
Okay.. I was actually trying to prove that no array trick mentioned by you, but wasn't sure if number m plays it's role in only one of the subsets.
Thanks a lot for clarifying. :)
thanks your approach was really nice.just one more thing would this have worked in case m & w could be of order 10^18? in case it wouldn't what should be the approach? thanks.
No it won't work in that case . Because this solution is based on the face that for n==2 and n==3 the answer is always "YES". and for n>=4 we see that 10^9 < n^15( 4 <= n < inf) . So the 2^elem recursion is under time limit .. But for 10^18 it would be 10^18 < n^30 or so for 4<=n<inf and so our solution may get TLE ...
Also another problem would be that the sum of subsets may exceed the range of long long(in c++).
In case of n,m<=10^18 this solution may do fine ( i think so!!! ). I have added all the necessary comments in the solution. It's based on — wrick's solution ...
Thanks again. :)
nice explanation dextrous !!!
U were the creator though ! Thanks for the solution ...
I too got it accepted(during the contest) using the same concept.
In case anyone wants to view the solution: http://codeforces.com/contest/552/submission/11647268
Nice Approach .
Thanks for sharing your solution .
Why will the higher powers of n not be useful in contributing to the weight on the either side?
Wild_Hamster Many solution get AC below 3 sec.So TL 3 sec not enough to block the n^3/6 solutions.
UPD: Now I see some solution gets AC in 1.1 sec .
But in C++ O(n3) solution is even faster than supposed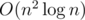 solution :)
solution :)
P.S.: Really nice contest! Thanks to the author!
Lots of STLs and calculations. You would not need most of them. :)
Check mine: 11652073
It was great contest especially the A,B and C problems can be solved in math ways :)
For problem D, I had a O(n*x[i]*y[i]) solution:
11646915
I wish this code was in C++!
I don't know if there's a way to make array starting from -200 instead of 0.
Yes there is. Let's say you need an array from -100 to 100. Make an array of size 201. Then every element can be accessed with the invariation A[X] = array[100+X]
As your wish, my O(n*x[i]*y[i]) code in C++
11655572
I think that it's not exactly right complexity. As I understand, it's O(n^2*log(max(x, y)) + n * x * y)
It can be done in O(n^2 +n*x*y) !!!
my code : 11655572
hello
in problem D , can anyone explain how to check the number of point that lay in each line in log(n)
thanks
Can anyone explain me the solution of C 11641785 by I_love_Hoang_Yen , the attempt part and the prove that it will give correct answers?
This brute-force solution. O(3 all.size())
Can you explain more in problem C. I am not getting when it is not 0/1 what are you saying. Plz explain something more means idea and concrete proof briefly
Unable to parse markup...
please fix this:) Wild_Hamster
Can someone please explain me why the time complexity of 552D for the solution mentioned is O(n^2*logn)?
Well , i would try to explain my approach which is O(n^2*logn) .
What I did is for each i , I calculated the slope of all lines taking ith one and all upto n . Then , total number of triangles having ith one as the vertex would be (n-i)C2 .. then i stored all the slopes in the map !! for all the lines having same slope , would not form a triangle , hence subtracted from the answer .
thus it was a O(n^2*logn) approach !!! check 11649484 this for better understanding and tell me if not clear .
n^2 for the nested loops and log(n) for the map used ...
Yhis is in accordance with the solution given by Meintoo above ...
Could someone please share their/an implementation of the editorial for C? I am struggling to implement the idea.
I explained the approach in this code ... ( using comments and examples ). You may go through it !
Thanks for providing solutions but I think it makes more sense to actually submit them to CF instead of putting to ideone. In this case we will be able not only see the code but also see the time and memory consumed by your solutions (and their own output in case if multiple solutions are allowed).
Java solution O(n^3) for problem D works :) 11671766
Could you explain your code please? :) Any idea why my code is giving a TLE?
From your code
area(x1, y1, x2, y2, x3, y3) = x1 * det(y2, 1, y3, 1) — y1 * det(x2, 1, x3, 1) + det(x2, y2, x3, y3)
So, area(x1, y1, x2, y2, x3, y3) = x1 * y2 — x1 * y3 — x2 * y1 + x3 * y1 + x2 * y3 — x3 * y2 = (x2 — x1) * y3 — (y2 — y1) * x3 + x1 * y2 — x2 * y1
Let a = x2 — x1, b = y2 — y1, v = x2 * y1 — x1 * y2 (or v = a * y1 — b * x1). We may not calculate these values everytime in inner loop.
area(x1, y1, x2, y2, x3, y3) != 0, so a * y3 — b * x3 != v
There are a lot of operations (additions and multiplications) in inner loop, so your code is giving TLE.
P.S. Sorry if my English is bad.
Can someone explain me this code for Problem D : http://codeforces.com/contest/552/submission/11636769
I know that he is calculating the equation of the line .. But how trip (variable) is working here and also about ans -= trip/3 .... Thanks in advance :)
Considering each point as a starting point he is iterating through all the second points to define the line that he would be considering. tp defines the equation of the line that he is considering and cnt[tp] the number of ending points considered till now that give the equation tp for the given starting point.
Let L be the set of line equations for the given starting point.
Notice how he does trip + = cnt[tp] before incrementing the value of cnt[tp].
So for each starting point he actually adds the value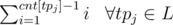 to the variable trip.
to the variable trip.
That is the same as adding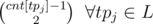
Okay so he has considered all the collinear triangles that he could have made. However, he has overcounted a little as he has counted a collinear triangle of the form: A – B – C thrice because he has counted this triangle once with A as a starting point, then B as a starting point and C as a starting point . So trip should be divided by 3 .
Obviously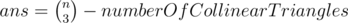
Thanks a lot !!
Zlobobers code for problem D gives compilation error on ideone
Can somebody explain why the complexity of E was O(|s|*17^2) !
It is given that max number of * signs are 15. In the editorial solution we are appending a 1 * at the beginning of the expression and a * 1 after the expression as that won't change the result. So the the number of * signs can be 17 now.
Then the code is something like this:
Hi everyone,
I'm trying to understand problem D (Vanya and Triangles) but I really can't get it. What does it mean "If some line includes x points, then in fact we counted, that it has 2 * x * (x - 1) points, because we included each point 2*(x-1) times in this line."?
I've tried looking at this solution http://codeforces.com/contest/552/submission/11663734 and I kind of get what he did even if it's not clear what exactly the normalize table does for me.
Can someone explain me more clearly?
For each pair of points get the equation of line (ax + by + c = 0, make sure a, b, c are coprime, i.e. convert 2x + 2y + 2 = 0 to x + y + 1 = 0). Now map this line with these 2 points. After processing all the points, if some line actually contains K points, we would have added 2*K*(K-1) points since we were processing each pair of points. We could have used a set to store the K points but that would add an extra log factor. Code
but in your code, you checked i*(i-1)==no.of points, doesn't it be 2*i*(i-1) ??
for (int i = 1; i <= n; ++i) { if(i * (i — 1) == points) { point_cnt = i; break; } } ans -= nc3(point_cnt);
Sorry for the confusion, my implementation is a bit different from the explanation. It's because I didn't use all n x n pairs of points to create lines, I only used C(n, 2) pairs. Check this part:
In this case, if a line contains k collinear points, there are C(k, 2) ways of choosing a pair of points and for each of these pairs, 2 gets added. So, in total, we have 2 * C(k, 2) instead of k. Hope it is clear now.
got it...thanks
I ways get a wrong answer on case 41 in problem E ,can anyone help me to check my program. http://codeforces.com/contest/552/submission/11986906
Thank you :)
how can E be done by brute force?
Man I can't understand a thing from those solutions, this editorial should be way more clear
Can someone please explain me how to turn some value into a w-ary representation? Because as I know it's always possible to turn any number to only BinaryRepresentation, sorry for my English if there're some mistakes. Thanks in advance!
I solved C a bit differently. Looks like it isn't mentioned in the comments. Apologies if I missed it. So if
n = 2the answer always exists. Fromn = 3let's find the sums of all possible subsets of (w^1, w^2, w^3, ...). We only need at most 20 because after that it exceeds10^9. (This limitation is actually a bit more complicated than that but let's assume it works). Because there are only 20 of these values, one can generate sums for2^20subsets within the time limit. Ifmis present in one of these sums, then the answer is YES. Or if the difference of sums for two subsets is m, the answer isYES. One additional condition to look for is that the subsets must be disjoint. Because you can't have the same weight in both the pans. So for each sum in the found sums array, check if a subset with sum =m - sum[i]exists and see thatposition_of_found_sum & iis 0 (disjointness).