558A - Lala Land and Apple Trees
Let's divide all the trees into two different groups, trees with a positive position and trees with a negative position. Now There are mainly two cases:
- If the sizes of the two groups are equal. Then we can get all the apples no matter which direction we choose at first.
- If the size of one group is larger than the other. Then the optimal solution is to go to the direction of the group with the larger size. If the size of the group with the smaller size is m then we can get apples from all the m apple trees in it, and from the first m + 1 trees in the other group.
So we can sort each group of trees by the absolute value of the trees position and calculate the answer as mentioned above.
Time complexity: 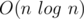
558B - Amr and The Large Array
First observation in this problem is that if the subarray chosen has x as a value that has the maximum number of occurrences among other elements, then the subarray should be [x, ..., x]. Because if the subarray begins or ends with another element we can delete it and make the subarray smaller.
So, Let's save for every distinct element x in the array three numbers, the smallest index i such that ai = x, the largest index j such that aj = x and the number of times it appears in the array. And between all the elements that has maximum number of occurrences we want to minimize j - i + 1 (i.e. the size of the subarray).
Time complexity: 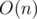
558C - Amr and Chemistry
Let the maximum number in the array be max. Clearly, changing the elements of the array to any element larger than max won't be optimal, because the last operation is for sure multiplying all the elements of the array by two. And not doing this operation is of course a better answer.
Now we want to count the maximum number of distinct elements that can be reached from some element ai that are not larger than max. Consider an element ai that has a zero in the first bit of its binary representation. If we divided the number by two and the multiplied it by two we will get the original number again. But if it has a one, the resulting number will be different. So, for counting the maximum number of distinct elements we will assume ai = x where x has only ones in its binary representation.
From x we can only reach elements that have a prefix of ones in its binary representation, and the other bits zeros (e.g. {0, 1, 10, 11, 100, 110, 111, 1000, ...} ). Let's assume max has m bits in its binary representation, then x can reach exactly 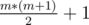 distinct elements. So, from each element in the array ai we can reach at most
distinct elements. So, from each element in the array ai we can reach at most 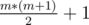 elements.
elements.
So, Let's generate the numbers that can be reached from each element ai using bfs to get minimum number of operations. And between all the numbers that are reachable from all the n elements let's minimize the total number of operations.
Time complexity: 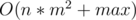
558D - Guess Your Way Out! II
First, each query in the level i from L to R can be transmitted into level i + 1 from L * 2 to R * 2 + 1, so, we can transform each query to the last level.
Let's maintain a set of correct ranges such that the answer is contained in one of them. At the beginning we will assume that the answer is in the range [2h - 1, 2h - 1] inclusive. Now Let's process the queries. If the query's answer is yes, then we want to get the intersection of this query's range with the current set of correct ranges, and update the set with the resulting set. If the query's answer is no, we want to exclude the query's range from the current set of correct ranges, and update the set with the resulting set.
After we finish processing the queries, if the set of correct ranges is empty, then clearly the game cheated. Else if the set has only one correct range [L, R] such that L = R then we've got an answer. Otherwise there are multiple exit candidates and the answer can't be determined uniquely using the current data.
We will have to use stl::set data structure to make updating the ranges faster. In each yes query we delete zero or more ranges. In each no query we may add one range if we split a correct range, so worst case will be linear in queries count.
Time complexity: 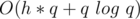
558E - A Simple Task
In this problem we will be using counting sort. So for each query we will count the number of occurrences for each character, and then update the range like this
for(int j=x;j<=y;j++)
cnt[s[j] - 'a']++;
ind = 0;
for(int j=x;j<=y;j++)
{
while(cnt[ind] == 0)
ind++;
s[j] = ind + 'a';
cnt[ind]--;
}
But this is too slow. We want a data structure that can support the above operations in appropriate time.
Let’s make 26 segment trees each one for each character. Now for each query let’s get the count of every character in the range, and then arrange them and update each segment tree with the new values. We will have to use lazy propagation technique for updating ranges.
Time complexity: 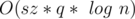 where sz is the size of the alphabet (i.e. = 26).
where sz is the size of the alphabet (i.e. = 26).











Thank you for Fast editorial
We have no rights to see the solutions. Please, change it.
Sorry, fixed.
For problem C, wouldn't a bruteforce on bits have a complexity of O(n*m) where m is the number of bits?
Yes, it can be done in O(n*m).
I loved the round! No issues during the contest (not with the statements, not with cf), an engaging problem set, and if it weren't enough, a lightning fast editorial publication. This is how a round should be done. Keep up the good work! :)
Can this solution work for Problem C:- For every element, find all the number that can be reached by applying the two operations between 0 and MAX and add one to each number's position in an array(lets say arr). Hence, we will have an array arr, which will tell us for each number i, how many elements given to us are reachable from i. So if we iterate over i from 1 to MAX and arr[i]==n, That means all the elements can be reached to i performing the operation. Then in n*log(n) complexity find the number of operations to convert all number to i and then print the minimum. Please tell me what is wrong with this approach.
It works.
Can you help me, with my submission then. http://codeforces.com/contest/558/submission/12060079 Thanks
You can reach 4 from 3:
3->1->2->4
After dividing, you should try to multiply again
The problem with your code is it will never reach all the possible numbers. For example if you take a test case n = 3 and elements as 11 10 21 In this case your answer will give answer as 4 considering all the numbers to reach 5. But the correct answer will be 3 because you can convert 21 to 10 in 1 step and 11 to 10 in 2 steps namely :- 11->5->10
So in the step when you are dividing by 2 i.e. p=p/2; you have to consider whether the previous p was even or odd. Since if previous p was odd e.g. if you have p = 11 then you will get different numbers by doing 2*(p/2). In this case 11/2 = 5 and 5*2 = 10. So you will have to find all the numbers <= Max in the step p = p/2 if p is even...
Also just try to debug with the example case of n = 3 and elements as 11 10 and 21. Try to print all the numbers element 11 is reaching according to your code and you will find that it is not reaching 10. That is the mistake.
I also did it in this way. You can check my AC code here. :- http://codeforces.com/contest/558/submission/12058744
Feel free to ask something you didn't got in this comment.. Hope it helps :)
Interesting round Waiting for your next :D Thank you
Problem C can be solved in O(NlogN). Imagine it as a binary heap such that according to the given operations, we can either go up to the parent( divide by 2) or to the left child (multiply by 2). Using such imagination, it can be solved as follows :
For each i, let
L[i] = Number of active nodes in left subtree of i
R[i] = Number of active nodes in right subtree of i
H[i] = Number of times i occurs in the input.
where a node is active if it occurs in the input.
We can calculate the answer if all of them are brought down to 1 using the level of each node.
Hence, now we move from 1 to the direction of optimal answer in the following way :
Here is a link of AC submission http://codeforces.com/contest/558/submission/12053885
Could you explain how your code is working?
The above picture shows the possible operations. Let ans[i] denote the answer if all of them are made equal to i. ans[1] can easily be computed using the levels of the nodes.
Now, We need to go from 1 to the optimal answer.
We can move from a node to its right child in search of the answer only if there is no active node outside the right subtree because there is no directed edge between from a node to its right child, hence there doesn't exist any path from outside the right subtree to inside the right subtree. Also, in such a case , we do not need to look for the optimal answer outside the right subtree because all the active nodes lie inside the right subtree and thus moving to right subtree must decrease the answer.
If we cannot move to the right child, then we go to the left child and compute it's answer and compare with the minimum.
Also, the answer of a child from its parent can be computed using
answer of child = answer of parent — Decrease in no of times we need to traverse the edge between child-parent.
Hope the approach is clear now. :)
Really appreciate your effort! Thanks! :)
Really cool solution :)
Not able to understand this line in your code.
Why are you using if(R[i] || H[i])up = true; ?
I think using if(H[i]) up = true; should be sufficient.
Please help me understand this line of code.
H[i] represents the count only of that node while R[i] represents the count of the right subtree. Up is true if we can enter the subtree from anywhere "outside" it. Outside means not just the immediate parent (represented by H[i] ) but also anywhere from the right subtree (represented by R[i]).
Very nice approach, thank you.
What's
UPbruh?C in linear time:
Let's create a binary tree with at least MAX_Ai nodes. With dp for every vertex we can say "what is a cost to move everything from its subtree to this vertex". Then from top to bottom we can do second dp — what is cost to move everything from outside of a subtree to this vertex? In my implementation rec(int,int,int) gets index of vertex, cost so far and number of elements outside of current subtree (cost increases by this number when we go to a child) Link: http://codeforces.com/contest/558/submission/12047835
and E without sqrt decomposition and lazy propagation: http://codeforces.com/blog/entry/19173?#comment-240849
Can you visualize your algorithm? I don't really understand from your code. Thanks for your attention
Let's say input is n = 3 and array 2,5,6. Consider a binary tree with 7 (in my code there are always 2^17-1) nodes where node number x has children 2*x and 2*x+1. Root has number 1. Now let's think about it as a graph. There is one "thing" in node number 2, one in node number 5, one in node number 6. What is a node minimizing sum of distances to these "things"? Draw it, it will help you to understand it.
Do you see a solution if we could go to parent and to each children? It would mean that we can do operations: x=x/2, x=2*x, x=2*x+1. The last operation means going to right child. Here we can only go up to parent (by dividing by 2) or to the left son (multiplying by 2). There is a small 'if' in my code for that.
I am not able to understand your code. Can you please explain what is stored in array res[]? I got that, the array ile[i] stores the number of elements in the subtree of vertex i.
res[x] is a cost of moving everything in a subtree x to vertex x
res[2*x]+res[2*x+1] is a cost of moving everything from a subtree 2*x to vertex 2*x plus the same for 2*x+1. Then we must move things from 2*x and 2*x+1 to vertex x. There are ile[2*x]+ile[2*x+1] things and we must move each of them by one (from 2x to x or from 2x+1 to x)
Can someone please tell me why this solution for D does not work ? (leftt is the starting index of the leaves and rightt the the last node) 12052248
Tanks a lot! :-)
In problem D you may get rid of h * q part by doing single jump from level i straight to leaves (12051754).
your code is what I call "code smart not hard". Nice code (Y)
Can you tell me why my code exceeds the time limit? Code
I don't know exactly but there may be the case when while(1) will cause an infinite loop so be careful with it. Also when you iterate through invalid vector, then you call dissolve function which catches two itr and itr2 "pointers" and then you iterate through it, I think this may not always be O(nlogn) algorithm, also there can be cases when you don't remove any segment from set s, and just split one segments into two parts and increase its size by one.
Anyway, keep going!
Thanks for the tips, I'll revise my code. As for the O(nlogn) part, I've noticed that the setter's code uses a similar sweeping algorithm though.
Why is q=0 in D (and E) allowed? Both are pretty dumb problems with q=0, and passing q=0 seems to be largely a matter of implementation (e.g. whether you include a "null" query of the whole range to begin with), rather than actually thinking about this possibility — I'm interested to know how many people actually noticed its allowed.
Am I going to have to look at lower bounds as well as upper bounds now? :P
Also just to give another idea for D — instead of keeping a set of segments that is good, you can keep a differences array — to make a segment [a,b] good, do val[a]+=1, val[b+1]-=1 — and take partial sums afterwards. Any good point is one where the sum there is q. (as a sidenote — it seems people who failed for q=0 did this idea without a null query)
Maybe there was no point in task E. But for task D those constrains will allow h = 1, q = 0 testcase which is interesting. :P
if (has[where]==maxn || val.count(has[where]+1)) can you please explain me second condition..
We are only storing a few values in this map (since there are like 2^49 leaves and we cannot store them all), so if val[x]=q, then also we know that for every x+1,x+2,... until the first one that has a different value in val also should satisfy val[x+i]=q (basically if the answer is unique, it must have val[x]=q, and also val[x+1]!=q).
ok got it... thanks...
Can someone explain how we are updating the segment tree in E? EDIT: Got it :)
I used the same way in problem C as the Editorial but I wasn't sure that there was no optimal answer above the max element ... my solution passed pretests but got TLE in test 21 ... i want to know why the number can't be greater than the max number
If you multiply the largest number by 2, you must multiply the other numbers at least once, right? Now suppose that you multiplied all the numbers by 2, you can get rid of that multiplication and improve the answer ( minus n moves)
If a*2=b*2=c*2=......=z*2 then a=b=c=...=z
12061940, working perfectly on my system but WA at #1. Please help
If neg and pos have the same size, you shouldn't add 1.
Duh,Me a noob! Thanks
Should the following input have an output of "cheated"?
Yes, it contradicts itself.
I Wrote the same damn code and it gave me wrong ans in A.
If l and r is the same, you can instead use b[i]+a[i-1]. That's why your answer is slightly smaller than jury's answer.
My solution for E is to deal with buckets.
First, count all the characters in the range.
If you have to count the whole bucket, use the precalculated counts(the one you use in counting sort). If you have to count individual alphabets in a bucket,
1) if sorted, use counting sort to pick one.
2) if not sorted, use the table(the naive one).
Now you have to recalculate the table.
If you have to update the whole bucket, use the idea of counting sort.
If you have to update individual alphabets,
1) if sorted, use the precalculated counts to write the table(the naive one). and do (2).
2) naively write the alphabet in the table(the naive one).
Problem C: I don't get the statement "From ai we can only reach elements that have a prefix of ones in its binary representation, and the other bits zeros." Say ai = 1101, then can't you reach 11010, 110100, etc.?
Problem C, setter's code, line 58. Why is it x > 100003, and not x>100000 only?
In div2-C tutorial :
Clearly, changing the elements of the array to any element larger than max won't be optimal, because the last operation is for sure multiplying all the elements of the array by two. And not doing this operation is of course a better answer.
can this thing be proved ?
All numbers can be written in the form n*2^k, where n is odd. For every number to be the same, they clearly need to have the same value of n. The only way to change the value of n is to divide by two. So this is the only operation we should do until all numbers have the same value of n. Once this is done, we need to make all the k the same. This is done optimally by finding the median number and making everything equal to that. So anything larger than the median, we divide by two until it is the same as the median, and multiply by two for anything smaller than the median.
When we make all n the same, clearly all numbers are decreasing. When we make all k the same, clearly all numbers are moving towards the median (which is less than the max). Hence, we never need to exceed the maximum number.
thankyou , i got the point :)
I don't get the C at all. Could you write that more formally? So many solutions here, but with so vague descriptions! Argh :(
"assume ai has only ones in its binary representation" — What do you mean by that? What if ai = 5?
Also, what do you mean by "ai has elements"? What are the "elements"? And why then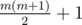 ?
?
Thanks in advance!
Okay, at last I got it. Thanks everyone for sharing ideas :)
Editorial enhanced. If there is any problem tell me.
"assume ai has only ones in its binary representation" that's only for analyzing running time, not the solution.
To solve Problem E, making a balanced binary tree that each node discribe some same character which located contigeously is much better than 26 segment trees, though both of their time complexities are O(sz*q*logn). It must because of the quantity of balanced binary tree is usually much less than segment tree. However, if it is sorting a long substring, balanced binary tree would delete many nodes and insert no more than 26 nodes; but the quantity of segment tree would not reduce.
There is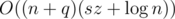 soltuion in E. It's similar to this solution. The difference is that we have only one set, each element of it describes a segment [l, r] with letter c.
soltuion in E. It's similar to this solution. The difference is that we have only one set, each element of it describes a segment [l, r] with letter c.
Because of using only one set we get rid of multiplier sz in complexity.
Solution works pretty fast on testcases (186 ms).
In your code, each query you need to insert a node into "set <pair <pair <int, int>, int> > s" at most 26 times. So why your complexity is O((n+q)(sz+logn))?
Yeah, thanks, you're right, I had slow implementation of this moment.
You can notice that elements we want to insert are in sorted order. It allows us to insert it in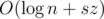 with second method from here.
with second method from here.
You can find new code here.
Thank you, I got it. I didn't not stl set can be used like this before. I can only write a splay tree so that realize O(logn+sz)....... Till now my program is the fastest in this problem, but a little long.
I did what Errichto explained but it was difficult atleast for me to implement in Java. But after some non-AC submissions, here is my submission: 44188936. I hope it helps.
But I still have one doubt about its complexity. It is amortized and range gets bigger as we do queries and hence query time reduces after every query. Is this the reason or is there some better/other reason?
Problem D (558D - Guess Your Way Out! II) looks like an exersize on compressed segment tree.
Let's tree(x) = 1 if an exit can be in x's leaf node and 0 otherwise. Segment tree will count sums of segments of function "tree". Initially tree(x) = 1 for all x in [2 ^ (h- 1); 2 ^ h- 1]. If the next query's answer is 1 then we need to assign tree(x) to 0 for all x in [2 ^ (h- 1); l- 1] v [r + 1; 2 ^ h- 1] where [l, r] — the segment on the h'th level of current query. It can be done with 2 queries to segment tree. And if answer is 0 then we need set tree(x) to 0 for all x in [l; r], we can do it with one query to segment tree.
Eventually sum of tree(x) for x in [2 ^ (h- 1); 2 ^ h- 1] will give the result.
Time complexity: O(q * h)
Memory complexity: O(q * h)
Implementation: 12067778.
There were some problems with memory, becaure each query to segment tree can add up to 2 * h new nodes in tree and each query with ans = 1 creates 2 queries to segment tree. Let process the queries with ans = 1 at first, we just need to intersect all segments of these queries. [L; R] is the result of intersections. After that we can build segment tree on segment [L; R] and process the queries with ans = 0. They creates one query to segmeng tree only.
Implementation: 12068161
For D, the second part can be done easier (without dealing with stl:set / range deletion) with an offline approach — just sort all queries with ans=0 by left coordinate and then sweep from left to right, computing the number of possible exits.
can anybody help me?
why my code for problem C is wrong?
my solution is O(N.logN) and i saw many people that thay solved like me but i get WA in test 7.
why?
I am not able to get where I am doing wrong in solution for problem A. Here is my solution. Can anybody please help me. http://codeforces.com/contest/558/submission/12052565
Did you forget sorting the array?
I want to mention that editorial code for problem D doesn't have really good decomposition and it makes it hard to understand how it solves the problem. Anyway, problems were really interesting and tricky a little. Thanks!
For problem D, Is the exit always on a leaf in the last level? I don't think it's specified in the problem statement, but correct me if I'm wrong. Thanks
"exit from the tree is located at some leaf node" this is clearly written in the editorial.
Could anyone tell me where I am going wrong for C? My code fails on #7 http://codeforces.com/contest/558/submission/12073898
My approach: - Find the max value - For all number in the array, divide until 0 is reached and multiply by 2 until max is reached. Record every possible number that can be formed in pos[] and record how many steps it takes to get that number in moves[]. - Now select moves[i] such that moves[i] is a minimum and pos[i] is equal to n.
Consider if number is 7. You multiply by 2 and hence form :
7 14 28 56......
Then you divide by 2 and form:
7 3 1 0
However once you reach 3 you can also form :
3 6 12 24
once you reach 1 you can form
1 2 4 8 16 32 64...
I don't think you've taken these numbers in consideration.
In D if there are two ranges with yes=1 but do not intersect, then will answer automatically be "Game Cheated!"?
Edit: Finally AC.Answer is yes.
Can anybody explain to me the complexity for E? For count sort, even if the count of each letter is given, isn't the complexity of building the string O(|N|), where N is the size of the string? I didn't think that was fast enough, as if each query takes N at least, then the complexity is O(N * Q), no?
If you use segment tree, it will be O(N * (26) * log2(N))
In problem B Div.2 how to break ties if we have same j-i+1.Here's my solution.Got a tle. Solution
This part gives you O(n^2) complexity: for(int in : ind){ ... for(i = 0;i<n;i++){
You should calculate first and last occurrences of numbers at once for all numbers.
I cant understand editorial to problem C, can anyone explain it to me in detail? Thanks.
For every number A[i] marks all the points less than 10^5. marking should be like this:
mark all the multiples of A[i] (i.e x=A[i]. while(x<1e5) mark[x]++; x=x<<1;)
repeat the process for A[i]/2,A[i]/4 until A[i]/2^c>=1.
for every value of i(1..10^5) check if current i is reachable from all A[i] (if mark[i]==n yes otherwise no) (if yes , find the number of steps and compare it with the current minimum) ( These all values are pre-computed )
print min
Problem A can be solved in constant time, no need to sort the list of coordinates.
As you read in the values, keep count of those on the left (values are less than 0) and those on the right (x > 0).
1)if the left count is equal to the right count, return the left+right.
2)return Min(left , right) * 2 + 1
We must calculate sum of some values, not only count elements. min(left,right)*2+1 is ok for calculating maximal number of apples, not maximal sum of their values.
For problem E, we could just keep a Segment Tree for interval [1..n] and update for each query the "order" of the interval [i j]: non-decreasing, non-increasing, unchanged. While updating, in case we reach on a path from the root an internal node that is already marked with some particular order, we can just mark its two immediate descendents with that order, unmark that node itself and continue. Time to process queries is therefore O(q * log n).
After we are finished processing queries, we can just do a preorder walk of the segment tree and determine for each position in the string [1..n] what kind of sort-order it belongs to.
Finally we would start walking the input string, counting the number of occurences of each character. Everytime the sort-order changes (or we reach end of string) we just output the characters we counted in the proper order and reset the counters. Time to output is thus O(q * sz + n).
The total running time is O(q * (log n + sz) + n), slightly better than the one in the editorial.
I don't think your solution is correct. You won't be able to know which character is where after a sorting operation.
Hmm... Yes, you are right. Didn't think this through... Thanks for noticing it!
Still feel like we could get rid of a sz factor. I will post if I figure out how and maybe implement that time also.
Best, Mircea**Hmm... Yes, you are right. Didn't think this through... Thanks for noticing it!** **** Still feel like we could get rid of a sz factor. I will post if I figure out how and maybe implement that time also. **** Best, ** Mircea**Hmm... Yes, you are right. Didn't think this through... Thanks for noticing it!
Still feel like we could get rid of a sz factor. I will post if I figure out how and maybe implement that time also.
Best, Mircea
For problem D, Why don't we just simply divides "Yes" and "No" queries to solve this problem in O( Q ) complexity?
For example let me explain how it works by dealing with "YES". First we set l=2^(H-1), r=2^H, which means that the exit might located in range [ l, r ). Then we get a query like x, h, "YES", we update [ l, r ), like l = max( l, x<<h ), r = min( r, (x+1)<<h )
Then we deal with "NO" in a similar way, but let variables l and r means the exit might located in [ 0, l ) and [ r, 2^H ) instead, just like above we got l = min( l, x<<h ), r = max( r, (x+1)<<h )
At last we just check out whether the ranges we inferred from "YES" and "NO" queries have an intersection on not, and answer the question respectively.
Is there anything wrong in my solution? Tell me if you found it, thanks.
For dealing with 'yes' queries, you're right.
The problem is, for every 'NO' queries, the 'YES' segments will be cut into pieces. So we have to find which 'YES' segment should be removed or contracted, which needs the log complexity.
In my opinion, we can "ignore" the "YES" questions and deal with "NO" questions independently.
Maybe it can be known more easily if I draw a picture, consider the following picture when we have to "combine" two "NO" questions together.
( So sorry that I cannot upload the picture for some reason ) http://image17-c.poco.cn/mypoco/myphoto/20150719/22/17831074120150719220100041.png
In a word, when I deal with "NO" questions, there is radically nothing to do with "YES" questions.
And finally we got the ranges that predicted ONLY from "YES" questions or ONLY from "NO" questions then find their intersections. Sincerely looking for your comments!
Yes, you can combine NOs and simply invert them to get possible ranges. As NO queries can be intersecting(like 1-5, 3-7) or separated(like 1-3, 5-7), we'll have to combine intersecting ranges so that there are only 'unique'(and separated) ranges. It can be achieved by two ways:
1) For each range, find appropriate place to insert current range. We can implement it with std::set or such, taking O(Q lg Q) time.
2) Use prefix array; if the range is [L, R], add 1 to a[L] and subtract 1 from a[R+1]. Finally take its prefix sum b[i]=a[0]+...+a[i]. If b[i]>0, i-th position is in NO range. Using this, we can achieve O(Q) time. But the indices should be normalized(coordinate compression), so O(Q lg Q) preprocessing is needed.
If I didn't got your point or missed something, please tell me.
I got your point.
My algorithm cannot combine 2 separated ranges like ( 1, 3, "NO" ) and ( 5, 7, "NO" ) because it will produce 3 possible ranges but not 2!
Sincerely appreciate your great help!
Div 2 problem c : i tried solving it like the editorial, and i got TLE, can anyone explain to me why ? here's my submittion http://codeforces.com/contest/558/submission/12195929 and i tried calculating the complexity, like the editorial, it's O(n*m^2) but maybe it's too slow ? i mean m=15 and n=10^5 in worst case ... maybe i got something wrong. thanks in advance
You are getting TLE because of the calls to memset here :
Instead of that, try coloring the vertices with a new color on every call to bfs
Also this can get you RE since you are accessing the element in the array before checking for the array boundry
A better way to do it is :
Hope this helps you.
I have implemented the same solution as mentioned in editorial for problem "Amr and Chemistry" in python but it is giving me time limit exceeded. Any thoughts? My submission: http://codeforces.com/contest/558/submission/12208553
Also can anyone please tell me about how much the time limits vary based on language(e.g. C++ vs python)?
LOL
Problem E can be solved using Square root decomposition also . Here is my accepted solution : http://codeforces.com/contest/558/submission/33019142
558B what is wrong with my submission 65573215 ? Why WA8?
Oh, I've found mistake. it was
r[i]-c[i]instead ofr[i]-l[i]I found a very weird bug while solving E. My solution using lazy propagation to sort the string. This is my initial code which gave tle: code.
I thought my implementation might be wrong, but it was correct. I just removed the line with the while(st<r) ( just before the sorting block ) and it got aced.
My st is the start of the block and en is the end of the block where I will put my characters. It shouldn't be a problem because in the end the st becomes r....
( i thought that it might not be the case so I used this code to verify, and it was true that st was becoming r code you can see that I added an if condition in the end, the same as termination of while loop ).
Another weird submission, wierd submission 2 because of the while loop.
I am not sure what the problem is so any help would be appreciated.