Hello.
Last Satuday we had the Brazilian Sub Regionals for ICPC 2015/16, an online contest was held at the same day on uva online judge.
I'm creating this post so we can discuss the contest problems.
Can anyone give me a hint on how to solve "I — Ominobox", "G — Curious Guardians" and "L — Lottery"?
(The other problems we either have solved during the contest or have solved after, so if you need help with any other one, let me know)











L — lottery
Let's imagine we picked some subset of the N guys and sum their values. We will end with a string that indicates the ordered parity of this chosen subset (something like EOEEO...) where E = even, O = odd.
So the only way the organizers can choose a parity ordered set of K numbers and never pay is if that string didn't show up by choosing one subset of N values.
This reminds us of linear algebra — let us think as the parity of the numbers chosen by the N people as vectors. If those vectors can generate the whole space of
then all parity subsets are covered.
However there's a slight trick as we must choose a non-empty subset of people. In Linear Algebra the vector (0, 0, ..., 0) always comes for free, but in this problem he doesn't.
By the way, I dunno who was the author but I liked this problem very much.
PS: another hint
Offtopic: It's brunoja. You can check the authors at the website: http://maratona.ime.usp.br/vagas15.html
Hello , is a good explanation. In addition you can solve in O(N * K) using a bit fast xor operation in gauss elimination
Hi ivanilos,
I've been trying to solve this problem... Can you give more hints?
I'm confused, because the combinations of the vectors (people's numbers) can't be arbitrary linear combinations, right? The coefficients must be either 1 or 0 (the person was choose, or not).
Could you explain from the point of view of linear algebra?
Thanks in advance!
The key topic to use in this problem which is related to linear algebra is linear dependence.
We model each person as a vector. A vector is "useless" if it can be made from a linear combination of other vectors (that is, it is linear dependent from other vectors), otherwise it is necessary.
Now, let's say we have X vectors, none of which is {0}K, such that everyone is linearly independent. Since no vector can be made as a sum of other vectors (considering only to pick or not pick a vector) we will have 2X - 1 possible sums (you either take an element or not, but you can't take nothing, so it is 2X minus the possibility of no vector taken). If not, let's say that we have a vector Vdep (or a sum of vectors) such that
Then at least one sum repeats, which means we don't have all the subsets we need.
The last step is to get the value {0}K — to get him we either need some dependent vectors or the {0}K itself, or both. So we can treat the "discrete" structure of the problem as "usual" continuous vectors. We can check vector linear dependence using Gauss elimination — for a matrix with N rows and K columns this can be done in
or even
(see ecapia comment).
I don't know if there is some field of study related to "discrete linear algebra", but if there is there might be some better (and shorter) explanation. This is how I solved the problem though, hope it helped.
G — Curious Guardians
For any unrooted tree we can pick a root arbitrarily, so let's say 1 is our root. Let dp(N, K) be how many trees we can construct with N nodes other than the root and with the root having at most K children. Then the final answer we want is dp(N-1, K).
1 will have at most K subtrees as children. Let's pick the first one of them. Say it has i nodes in it. We can choose nodes to be in this subtree in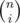 ways, then we can pick the root of this subtree in i ways, and fill the rest of the tree in dp(i - 1, K - 1) ways. The other subtrees that are children of 1 can be picked in dp(n - i, k - 1) ways.
ways, then we can pick the root of this subtree in i ways, and fill the rest of the tree in dp(i - 1, K - 1) ways. The other subtrees that are children of 1 can be picked in dp(n - i, k - 1) ways.
Maybe you realized this is actually overcounting some trees -- for example it considers 2-1-3 and 3-1-2 as distinct. If we have a problem because we are considering orders as distinct, let's force one order! Let's reorder the child subtrees of 1 so that, if you identify each subtree by its smallest node, they come in lexicographical order. This order is easy to achieve by forcing the smallest node available to go the first child subtree, which eliminates the double-counting.
Final solution:
Nice solution, in the contest i used an extra parameter and my solution was a little bit more complicated.
Hello everyone , I have founded other solution simpler. Imagine we have a partial tree , if I process in order from left to right about leafts I will never have count twice any tree so we just process one by one.
Let dp(n,k) be a tree which have k leafs and we want to add n nodes in those leafs, this will compute how many tree there will be with this conditions, so the answer will be dp(n-1,1) , as I said , if a process lefts in order I will never count twice some thing. In each configuration I try to add children en the first leaf of our current tree, also exist take nothing dp(n , k) -> dp( n, k — 1)
Final solution:
dp(n , k) = comb(n , children) * dp(n — children , k — 1 + children )
0 <= children <= min( (Is first node ? k : k — 1) , n)
The problem is equivalent to counting Prufer sequences where each of symbol appears (k-1) or less times, as the number of appearances in the Prufer code is degree — 1. So it's just counting the number of strings of length over symbols 1,2,..,n where each symbol appears k-1 or less times.
This then becomes a fairly standard string counting inclusion/exclusion principle problem, ie, Sum C(n,i)C(n-2,ik)(ik)!/(k!)^i n^(n-2-ik)(-1)^i.
Hah, I had this feeling that this problem had to have a cleaner solution, but I couldn't find it. Thanks a bunch for the pointer to Prufer sequences! :)
Edit: on trying to understand the inclusion-exclusion, are you not double-counting something? As in, the elements of the bigger than K groups and the rest are being permuted? I might need some more time to make sure but learning about these sequences was cool nonetheless.
Hi,
You are right, the formula is not quite correct, however with counting Prufer sequences, this problems simply reduces to the problem of ways of permutating n-2 elements picked from the multiset of {k*a1, k*a2,..., k*an}, where a1,..,an are the n labels. This can be solved with O(n^3) DP just like the tree problem.
A direct way of computing this though is using the simple generating function:
[ Sum over j (1<=j<=k) of (t^j / j!) ] ^ n
Let M be the coefficient of t^(n-2), then the answer is M*(n-2)! Since any time the coefficient goes over t^(n-2) in the computation, we can just drop it, we keep only O(n) terms each polynomial multiply, so the complexity of O(n log n) with FFT multiplies.
O(n log^2 n), in fact, because you need to do several multiplications. But while I haven't coded this (would be hard to do FFT with the modulo they used), this looks really likely to be correct.
I coded the FFT multiply solution, it got accepted: http://pastie.org/private/gumax8sj8m0dmwcssywvla
Why is FFT so slow u.u
Constraints are small, so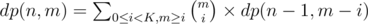 , where dp(n, m) is the number of sequences considering elements in [1, n], with length m and where elements repeat at most K - 1 times should do the job, and dp(n, n - 2) should give us the answer.
, where dp(n, m) is the number of sequences considering elements in [1, n], with length m and where elements repeat at most K - 1 times should do the job, and dp(n, n - 2) should give us the answer.
This solution seems to be the simplest, but I can't understand the logic. Can you explain your math? Thanks in advance!
This solution refers to baodog's observation (Prufer sequences) that all sequences of n - 2 elements in [1, n] (possibly repeated) form a bijection with the set of all spanning trees of complete graph Kn. Moreover, v appears k - 1 times in those sequences iff node v has degree k in correspondent tree.
So we can count number of valid sequences using the given DP. If we have sequences of m elements using only elements labeled in range [1, n], we can add 0 ≤ x < K elements labeled n + 1 to it so we will have a new sequence of m + x elements using elements labeled in range [1, n + 1].
We should be able to add these new x elements between any of the elements of the former sequence. It's equivalent to the problem of interpolating two strings without changing their original orders. There are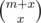 ways to do that. From that you can derivate dp(n, m) transitions easily.
ways to do that. From that you can derivate dp(n, m) transitions easily.
Hello,
I think that should be dp(i -1, K — 1) instead of dp(i, K — 1). [The rightmost recursive call]
Very nice solution, thanks (:
You're right, of course. Fixed.
Hi,
I'd like a hint to the problem A — Even Obsession.
Make a graph in which each vertex is (city, number of tolls is even or odd).
Then Dijkstra in this new graph can solve the problem.
Can someone give me a hint for Problem B — Stock Market ?
Use an extra parameter that says if you can buy/sell a stock.
It can be solved using DP. Each day you can either sell the stock (if you've already bought it before), buy it (if you haven't bought it already) or do nothing.
Can someone give a hit about problem K: Palindrome?
Dynamic Programming with states [left bound][right bound]. Try to build the palindrome from the borders. If both characters are equal, you can try to insert them in your current palindrome, otherwise, you have to 'discard' on of the characters. Remember that the problem asks you to minimize 2 parameters, used special positions and size, so you have to store a 'pair' as a state instead of a single digit. It is O(n^2)
Does uva online judge support virtual contest? Or maybe someone can upload it to gyms?
Near the bottom of the page http://uhunt.felix-halim.net/id/0 there is a virtual contest generator. You can get all the problems from this subregional automatically by looking for it under the "Past Contests" list.
It wouldn't be bad if someone could just upload it to gyms, though.
Idk what you need to do to upload it to the gyms, but in case someone wants to do it, the official in/out can be found here. (It's the "Entradas e Saídas" link next to each problem).
I believe you should also have a working solution, at least to measure time constraints. Which I'm not able to do since I haven't gotten my Ominobox to stop giving TLEs u.u
Hey guys. Any tips on solving the I — Ominobox?
I guess the trouble is to discover quickly the minimum height for each n-omino.
marcoskwkm? Help?
https://en.wikipedia.org/wiki/Polyomino
I pre-computed and stored the just the "free" polyminos (<5K for 10). This became fast enough for scanning through all the polyminos at each position on the grid. However, this seem to require a bit masking trick to work fast enough, and my code is a bit slow right now. Basically there are 8 orientations with rotation+flip. We have 5 bits (<30), so that fits in a long long. So we want to do single scan for all the orientations at the same time though grid, and do a min across each starting position of max of heights of cells.
Just create a bit mask for each row of up to each 30 heights of grid, and create bit mask of each polymino. Then binary search to see if each one can be placed at a certain height. On average only <2.5 binary search passes are needed for 30 height values. Here is the code:
Thanks a lot :) I was trying to do something similar but i tought the Binary search wasn't good enough for the time and the bitmasks got quite confusing. Your explanation was clarifying. Thanks.
I simply used a 1 to indicate "blocked" at that height and above, i.e.
Once I did this, the problem became really trivial. BTW, additional optimizations I haven't had time to try and is not needed is:
How to solve D? Is it gauss?
Read the statement more carefully.
but gauss would do as well, wouldn't it? It only has L + C equations and the problem says it's always possible to find a solution, so the number of variables is ≤ L + C ≤ 200, which is feasible with gauss elimination
Yes, it would. But in a time-limited contest, you don't want to miss the much easier solution because you didn't read one line, right?
Depends on the contestant. Some people might find easier to copy a gaussian elimination (or, in this case, just the back substitution step) implementation than writing/debugging the simulation solution for this problem.
But some should really avoid that, specially if the gaussian elimination implementation they have is a pretty buggy one made by their coach.
D is purely simulation. The statement is clear about the rules, specifically on this bit "it's always possible to find a row or a column where there's only one variable which its value is unknown". Therefore you should just find that variable, calculate it's value, and repeat this process.
alv-r, please give me your solution for Stock Marcket. Or a hint.
It can be solved with dynamic programming. The states can be represented by [current index][do I have have the stock ?], in transitions you can choose to buy the stock in the current day (in case you don't own it yet) or sell it (in case you own it).
The DP is something like this:
But (at least on uva) if you do it with recursion+memoization you'll get an Runtime Error because of stack overflow, so you gotta do it bottom-up. The following for loop uses the same idea, but without the recursion: