This problem can be approached from two sides - from a programmer's perspective and a mathematician's one. We consider both approaches.
First, let's write some general propositions. Let's put on a straight line all the moments of time when the trains arrive. We will refer the interval between two successive points to the girl, to who the train that matches the right end of the segment is going. Also note that the entire picture is periodic with the period equal to lcm(a, b). Vasya will obviously more often visit the girl, whose total length of the segments is larger.
The programming approach is about modeling the process. If we need to compare the lengths of two sets of intervals, then let's count them. We can do it using two pointers. Let's see what train comes next, add time before the arrival of the train to one of the answers, move the pointer and the current time. We should stop either when two last trains arrive simultaneously or when arrive a+b trains. The solution has asymptotic O(a + b), that fits the time limit. Don't forget that lcm(a,b) ~ 10^12, i.e., we need the 64-bit data type.
The mathematical approach provides us with a more elegant and shorter solution, however, it takes more thinking. It seems obvious that Vasya will more often go to the girl, to who trains go more often. This fact is almost true. Let's try to prove it. Let's divide a and b by their gcd - from this, obviously, nothing will change. To make it clearer, let a ≤ b. Let's calculate the total length of segments corresponding to the second girl. For this, we need to take a few facts into consideration.
1) All of them do not exceed a
2) All a segments are different (due to coprimeness of a and b).
3) They all are at least 1.
But such a set of intervals is unique - it’s set of numbers {1, 2, … , a} and its length equals
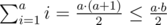 . Besides, the equality is fulfilled when the following condition is met: b - a = 1.
. Besides, the equality is fulfilled when the following condition is met: b - a = 1. Hence the following is true. The answer is Equal, when |a - b| = 1, otherwise Vasya goes more often to the girl to which the trains go more often. The key is not to forget to divide a and b by their gcd.
Problem Div1-B, Div2-D. Vasya and Types.
In this task, it was necessary to do exactly what is written in the problem's statement, for practically any complexity.
You are suggested to do the following. For each data type we shall store two values - its name and the number of asterisks when it is brought to void. Then the typeof request is processed by consecutively looking at each element of an array of definitions, in which we find the desired name of the type and the number of asterisks in it.
The type errtype is convenient to store as void, to which we added - inf asterisks.
Thus, fulfilling a typedef request, we find the number of asterisks in the type A, add to it a number of asterisks and subtract the number of ampersands. Do not forget to replace any negative number of asterisks by - inf, and create a new definition of type B, removing the old one.
Problem Div1-C, Div2-E. Interesting Game.
In this task you should analyze the game. However, due to the fact that with every move the game is divided into several independent ones, the analysis can be performed using the Grundy's function (you can read about it here, or here). Now all we have to do is to construct edges for each position. We can build the edges separately for each vertex by solving
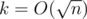 simple linear equations for each number of piles after splitting. We can construct all the divisions in advance, simply taking one by one the smallest pile and the number or piles and terminating when the sum exceeds n. The second way is better because it works for the O(m + n), where m stands for the number of edges, and the first one works for
simple linear equations for each number of piles after splitting. We can construct all the divisions in advance, simply taking one by one the smallest pile and the number or piles and terminating when the sum exceeds n. The second way is better because it works for the O(m + n), where m stands for the number of edges, and the first one works for  , which is larger.
, which is larger.We should evaluate m in the maximal test. The edges are no more than
 . However, in practice they are much less - about 520 thousand. Which is why there's enough time to build the edges within the time limit of O(nk).
. However, in practice they are much less - about 520 thousand. Which is why there's enough time to build the edges within the time limit of O(nk).You can try to find a Grundy's function by the definition if we xor all the required values for each position. But this may not work: it has too many long partitions (solutions with lazy countings or other ideas was working, though).
Let's learn how to quickly count a Grundy's xor function for a long partition. Let's use a standard method for counting functions on the interval - xor[l, r] = xor[0, r]\^xor[0, l - 1]. In the course of the algorithm we will keep a xor on a prefix of xor[i] up to i. Then the xor on the interval can also be calculated as O(1). The solution was strictly successful due to the number of edges, which is not very large.
Problem Div1-D. Beautiful Road.
In this task we should count for each edge the number of ways on which it is maximal. Since for one edge alone it does not seem possible to find the answer faster than in the linear time, the solution will compute answer for all the edges at once.
We shall solve the problem first for the two extreme cases, then, combining these two we will obtain a complete solution.
The first case is when the weights of all edges are identical. In this case we can solve the problem via DFS. For each edge, we just need to count the number of paths that this edge lies on it. This number is the product of the number of vertexes on different sides of the edge. If we count the number of vertexes on one side from it, while knowing the total number of vertexes in the tree, it is easy to find the number of vertexes on the other side of it, and hence the required number of ways on which it lies.
The second case - when the weights of all edges are distinct. Sort the edges in the order of the weight's increasing. Initially we take a graph with no edges. We add an edge in the order of increasing of weight. For each edge we join the connected components it connects. Then the answer for each new added edge is the product of the size of components that it has connected.
Now we must combine these two cases. We will add the edges in the ascending order, but not one by one, but in the groups of the equal weight. We should understand what the answer is for each of the added edges. After adding our edges some number of connected components was formed - for each edge, we calculate the same product of the number of vertexes on different sides inside his newly formed connected component.
To find this number of edges on the different sides, we should realize that it is only enough to know the sizes of the old connected components and connections between them - how they were arranged is not important to us. We use a DSU: adding an edge to our forest, we combine the old connected components by these edges. Note that prior to the merging of the components we must calculate an answer for our edges - and it is possible to make via a DFS on our compressed forest as in the first case, only instead of the number of vertexes on different sides of the edge we take the sum of the sizes of the connected components on different sides of the edge.
How to do it neatly:
- It’s good idea to dynamically create compressed graph at each step: it will have O(E’) vertexes and edges, where E' - the number of added edges of the source tree.
- Do not create unnecessary vertexes in the new created compressed column: after all, the DFS works for O(V + E), rather than O(E), so the unused connected components we do not include in the circuit.
- We should use the 64-bit data type. To store the response of the order of (105)2 it will fit more than the 32-bit one.
- We should not merge the adjacency lists explicitly when connecting components. It is too long.
- You can do everything instead of arrays on vectors / maps / heap, so the total time of nulling of the marks for an array of DFS occupied O(V). Or, instead of nulling of the array overlays we keep instead of a Boolean flag the iteration number. In general, it is better not to null extra arrays. After all, algorithm can make V iterations.
- Be careful, solutions with map works at TL's maximum, so it should be written very carefully; you should better use the vectors + list of involved nodes. The author's solution with the map fits in the TL with only half a second to spare. While using a vector has a four-time stock of time to spare.
Problem Div1-E. Mogohu Ree Idol.
In this task we had to verify that the point is the centroid of the triangle formed by points of the given three polygons. Lets reformulate the problem. We should verify the existence of three points A, B, C, such that A belongs to the first polygon, B - to the second one, C - to the third one, and 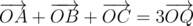 . Logically, you should understand what set of points determines this
. Logically, you should understand what set of points determines this 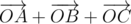 , you should understand how to build it and test a point on whether it belongs to the set or not. This set is called Minkowski sum. We will need only one of its properties: the sum of two convex polygons is a convex polygon whose sides coincide as vectors, with the sides of the original polygons. We will prove this later.
, you should understand how to build it and test a point on whether it belongs to the set or not. This set is called Minkowski sum. We will need only one of its properties: the sum of two convex polygons is a convex polygon whose sides coincide as vectors, with the sides of the original polygons. We will prove this later.
How do we use it now? The first thing that this property gives us is an algorithm to test for belonging. Once the sum is built you can test whether or not a point belongs to the sum using a standard algorithm of testing a point being inside of a convex polygon in logarithmic time. Also the constructing algorithm is immediately obtained. We just need to add the coordinates of the lowest (the leftmost of them) points of all three polygons. As a result, we get a point, which is the lower left for the sum polygon. The sides are now represented as a sorted by the polar angles list of parties of the original polygons (instead of sorting we may merge sorted arrays).
Proof.
We shall prove the correctness of the algorithm for two polygons, for three polygons the proof is just the same. Let the first polygon be represented by A and the second one - by B. Denote the sum as M.
We will prove that M is a convex set.
Choose some 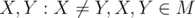 . By definition,
. By definition, 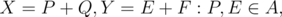 Q,
Q, 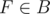 (here and below the point is identified with its radius vector).
(here and below the point is identified with its radius vector).
Let’s take some point 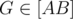 . We shall prove that
. We shall prove that 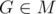 .
.
As G lies on the [AB], 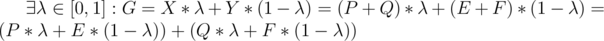 .
.
Note that the first bracket is obviously some point lying on the segment [PE]. That means the point lying inside the polygon A, since A is convex. Similarly, the second bracket is inside B. Hence, their sum, i.e., G, lies in the Minkowski sum. This means that the Minkowski sum is a convex set.
Let us consider some side XY of the first polygon. Let's rotate the plane so that the side XY was horizontal and that the polygon lied above the XY line.
Consider the lowest horizontal line intersecting B. Let it cross B along the segment of PR, where point P does not lie further to the right of the R (it is clear that PR can turn out to be a degenerate segment from one vertex or the segment between two consquent verteces). Let's call PR the lowest segment of the polygon. Then we construct in the similar way the lowest segment UV of polygon M.
Let's prove that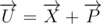 - if not, let
- if not, let 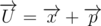 . It is clear that x and p are the lowest points of the polygons A and B - otherwise one of them can be moved to a small vector d, which lies in the lower half-plane, so that the point remained within its polygon. In this case U will move the same way to d, which contradicts the fact that U is one of the lowest points of the polygon.
. It is clear that x and p are the lowest points of the polygons A and B - otherwise one of them can be moved to a small vector d, which lies in the lower half-plane, so that the point remained within its polygon. In this case U will move the same way to d, which contradicts the fact that U is one of the lowest points of the polygon.
Thus, x and p are the lowest points of their polygons. Similarly, x and p are the leftmost points on the lowest segments of their polygons - otherwise we shift x or p to vector d that is directed to the left. It is also a contradiction - the U point stops to be the leftmost lower point.
Hence, U = X + P. Similarly, V = Y + Q. Hence, 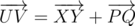 .
.
Thus, the sequence of sides M as vectors in the, for instance, counterclockwise order, is nothing other than the union of sides of A and B as vectors in the counterclockwise order, that immediately proves the correctness of the algorithm.











Sorry, we are soo sleeppy...
"Thus, the sequence of sides M as vectors in the, for instance, counterclockwise order, is nothing other than the union of sides of A and B as vectors in the clockwise order, that immediately proves the correctness of the algorithm.”
Yes, you're right. Fixed.
===
Well, there exist at least one human, who read that up to the end :-) Great.
thank you for good editorial. can you say what do you mean by position in problem Div1-C? Do you mean the size of each pile or some piles together?
Like in all problems that are solved using Grundy function, here position means "One pile of fixed size". It is true that if we have some piles of different sizes then games on each of them are independent — that's also the explanation why xoring of Grundy functions works correctly.
Thanks! I think i get the main idea of the solution!
For Div 2 C — Trains, is there a proof for the fact that the segment lengths will be different (as mentioned in the editorial)?
Yes, this can be proved by using the basic concepts of number theory. Let b > a, After dividing a and b by their gcd let new a = a/g, and new b = b/g, where g = gcd(a,b)
Now gcd(a,b) = 1. Let's calculate for each instance b, 2*b,.....a*b, the length of the segment.
For a*b the length of the segment will a. For i * b, i < a the length of the segment will be (i*b)mod a.
Let for two different instances i, j < a, the length of the segment is the same.
so i*b ≡ j*b mod a => i ≡ j mod a, as gcd(a,b) = 1, which is not possible as i and j are two different instances.
Thus the contradiction proves, for two different instances, the length of the segment cannot be the same.
A very clearly stated explanation. Thanks for the help!
I understand everything, but why Vasya has two girlfriends?