Problem A. PawnChess
Player A wins if the distance of his nearest pawn to the top of the board is less than or equal to the distance of the Player’s B nearest pawn to the bottom of the board (Note that you should only consider pawns that are not blocked by another pawns).
Problem B. The monster and the squirrel
After drawing the rays from the first vertex (n - 2) triangles are formed. The subsequent rays will generate independently sub-regions in these triangles. Let's analyse the triangle determined by vertices 1, i, i + 1, after drawing the rays from vertex i and (i + 1) the triangle will be divided into (n - i) + (i - 2) = n - 2 regions. Therefore the total number of convex regions is (n - 2)2
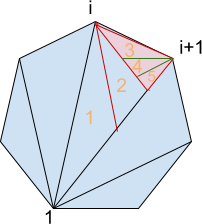
If the squirrel starts from the region that have 1 as a vertex, then she can go through each region of triangle (1, i, i + 1) once. That implies that the squirrel can collect all the walnuts in (n - 2)2 jumps.
Problem C. The Big Race
Let D be the length of the racetrack, Since both athletes should tie  .
.
Let M = lcm(B, W), then D = k·M + r. None of the athletes should give one step further, therefore r ≤ min{B - 1, W - 1, T} = X.
D must be greater than 0 and less than or equal to T so - r / M < k ≤ (T - r) / M.
For r = 0, the number of valid racetracks is 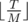 , and for r > 0 the number of racetracks is
, and for r > 0 the number of racetracks is 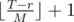 .
.
Iterating over all possible r, we can count the number of racetracks in which Willman and Bolt ties: 
Note that 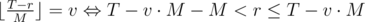 . That means that
. That means that 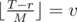 for exactly M values of r.
for exactly M values of r.
We can count the number of values of r in which 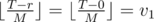 , and the values of r in which
, and the values of r in which 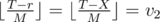 . Each of the remaining values v1 - 1, v1 - 2, ..., v2 + 1 will appear exactly M times.
. Each of the remaining values v1 - 1, v1 - 2, ..., v2 + 1 will appear exactly M times.
Problem D. Super M
Observation 1: Ari should teleport to one of the attacked cities (it doesn't worth going to a city that is not attacked since then she should go to one of the attacked cities)
Observation 2: The nodes visited by Ari will determine a sub-tree T of the original tree, this tree is unique and is determined by all the paths from two attacked cities.
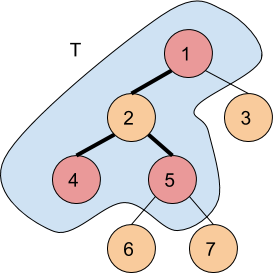
Observation 3: If Ari had to return to the city from where she started, then the total distance would be 2e, where e is the number of edges of T, that is because she goes through each edge forward and backward
Observation 4: If Ari does not have to return to the starting city (the root of T), then the total distance is 2e - L, where L is the distance of the farthest node from the root
Observation 5: In order to get a minimum total distance, Ari should chose one diameter of the tree, and teleport to one of its leaves.
The problem is now transformed in finding the diameter of a tree that contains the smallest index for one of its leaves. Note that all diameters pass through the center of the tree, so we can find all the farthest nodes from the center...and [details omitted].
Problem E. BCPC
Let’s represent the reading and writing speeds of the students as points in a plane. Two students i, j are compatible if ri'·wj' - rj'·wi' > 0 this equation is identical to the cross product: (ri', wi') × (rj', wj′) > 0. Using this fact is easy to see that three students i, j, k are compatible if the triangle (ri, wi), (rj, wj), (rk, wk) contains the point (x, y). So the problem is reduced to count the number of triangles that contains the origin.
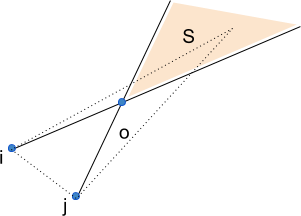
Let’s count the triangles that have two known vertices i and j (look at the picture above). It is easy to see that the third vertex should be inside the region S. So now we have to be able of counting points that are between two rays, that can be done using binary search (ordering the points first by slope and then by the distance to the origin).
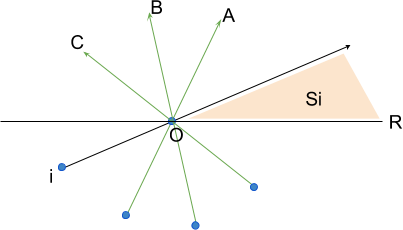
Now given a point i, let’s count the triangles that have i as a vertex (look at the picture above again). We have to count the points that lie between the ray iO, and every other ray jO (the angle between iO and jO must be ≤ 180).
Let Sj denote the number points that are between the rays OR and jO, then the number of triangles that have i as a vertex are 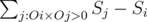 . This summation can be calculated if we pre-calculate the cumulative sums of Sj.
. This summation can be calculated if we pre-calculate the cumulative sums of Sj.
The overall complexity is O(n·log(n)).










Nice & creative problems!
Fast analysis, slow system grading :( hope everyone high rating
When does system testing usually finish? In 30 minutes?
No, it will finish tomorrow.
WHAT!!! I did a few contests half a year ago and testing took at most 1 hour! >_<
i solved B in diffrent way summation of odd number Link ;))
It is same, n^2 == sum of first n odd numbers
Yes thanks ;)
Can someone explain problem D in detail. I mean to say complete the details omitted.
Firstly, it is easy to see that we should start at an attacked city, because it would minimize the road we have to take. This give us the idea to cut away some part of the tree which doesn't contain any attacked city (in the test case above, is city 3, 6, 7), then we shouldn't care anymore about those thrown-away part. Now assuming that after we have throw away some part, we have a graph G(V, V-1). Assuming that we start our journey at some vertex U, and we have to come back to U after visiting all vertex in {V}, this would take us 2*(V-1) cost (Because we have to visit each edge once, and come back, so each edge would be visited twice). But we don't have to come back to U, so there are some edge we don't have to visit twice. In order to minimize the cost, we will visit all the edge in the longest path in G once. Let the longest path between any two vertex in G(V, V-1) (assuming it is X and Y) be LEN. Then the answer would be (2*(V-1) — LEN). You should also output min(X, Y).
Hope this help !
TooMedium Great! Thank you very mach :) All clear, but how to find this LEN? NP problem?
You can find LEN with this:
Choose a vertex U (not important which one you choose) and find the futhest vertex to U. Let's call this vertex as A. Then find the furthest vertex to A with same way. Let's call this vertex as B. The Longest SP between two vertices is the path between A and B. To choose minimum index (for A or B) it's enough to find the vertex with smallest index of furthest ones (both from U and from A).
In other words, it means to go along the longest path(say p) in the new tree and whenever there are branches in p(say b(i)) cover the branches first and return back to p which makes the total length traveled p + 2*b(i) for all branches i. But I still don't understand how that is optimal. Any help?
The vertices we travell along is a subtree of initial tree. And we start travelling from a leaf. We must go all the leaves. So let's call first leaf we travel on it (where we start) as S and the last leaf we travel as F. And P is the path between S and F. For branches of P we will travel on all edges twice (Going to leaf and coming back). So we are using all edges twice except edges in P. Total cost is 2*(edges in subtree) — L(length of P). So in optimal situation P is longest.
I got hacked on problem A for the case where the number of moves for 'w' and 'b' are the same by laablckdae. Figured it out and finally got my first chance to hack another user's submission. Unfortunately, it happened to be my friend fenil, who happened to be in the same hack room as me and also lives next door. Literally. Yes, he is quite upset :P
Problem C was so tricky!! If you didn't have bignum implementation for C++ (like me) and didn't want to think about the problem, you should have used another languages which have bignum inside such as python! but .. a lot of people didn't want to use python and failed in system testing because of overflow problems!! If only limits where 1e9, a lot of people wouldn't failed!
PS: I myself learnt python during the contest :\
I used Russian Peasant for Multiplication but later realized it was not necessary.
How is Russian Peasant used to avoid overflow if the end result is larger than unsigned long long ? for example a*b here where both a and b are 10^18
I used the same idea 13986831, the trick is that when you use this technique, the result grows slowly enough that you can do an early break once it exceeds t.
I'm not sure if what I did is the same as Russian Peasant Multiplication, but I'm essentially doing binary exponentiation with multiplication replaced by addition.
I get it now ... this should come in handy in future problems . Thank you :)
I used it to know if LCM(w,b) is greater than t or not.I used unsigned long long. It's more than 18.4e18 . Inputs are 5e18 . In first step you add some value X to the result and in the next step add 2X to the answer and then 4X and so on. Say your latest addition was X to the result that did not cross 5e18 but was very close to it . your next addition will be 2X . So, In worst case result will become something like 15e18. So,stop the calculation as you know the result will definitely be larger than what you needed.
I used
doubleto store the product of two numbers of the order of 10^18.Solution link: 13987689
Because you actually don't need the LCM (= w/g * b, where g = gcd(w,b)) when lcm > t, you can actually just do a check like this: if (t/b <= w/g) do lcm stuff else do without lcm stuff. Because you use division (also, you can verify that it is correct even with integer division truncation), it will not overflow. Problem solved :) 13998172
in problem C test case #24 : 1000000000000000000 1000000000 2000000000 could someone please explain the output 1/2 ?
It's simplified
Reading and writing speed being negative, student with reading and writing speed equal to -10 overwhelms one with reading and writing speed 5... Yes, this is definitely the worst story I have ever ever read ._. ...
Please explain test case in a detailed manner i am very confused in this test case it will be helpful for me 4000000000000000000 9999999999999997 99999999999999999
It means that each step of Willman is 9999999999999997 and that of Bolt is 99999999999999999. So if the total length is less than or equal to 9999999999999996, then either of them taking the step results in falling into the abyss. Hence, they don't take the step resulting in a tie. After that, upto a length of 99999999999999998, Willman can take the jump while Bolt has to stay at the starting point. So, Willman wins. On increasing the length, Bolt can also take the step causing him to win. Now, since the LCM of both their steps is very large, none of them will have the same stopping point again and no ties will occur henceforth. Hence, the probability of a tie is the simplified version of: 9999999999999996/4000000000000000000.
Actually gcc has an built-in function for checking overflows:
__builtin_mul_overflow,which computes the product of the first two argument(of any integral type) with infinite precision , give the value to what the last argument (a pointer to any integral type) points to and returns true if the last step causes overflow and false otherwise. Check this article on gcc.gnu.org for details and 13998217 (which is 13994692 with some modifications) for how can it be used on Problem C.I feel editorial given here for problem D is not sufficient. Can someone explain it ??
I could not understand observation 2 of problem D.
Can anyone please explain how can we generate the sub tree with bit more details?
remove all the nodes from the tree that are not marked and not between two marked nodes.
If you connect all the nodes that have been attacked then you get a unique tree.Uniue here means that the total length of tree is fixed.
Here from observation 1 it is clear that one of the nodes attacked have to be the starting point. So we are basically making one of the node the root and calculating the complete length of the unique tree.Suppose if the node attacked are:1 2 3 and tree is 1 2 1 3 then the total length of path=4; This is because of the fact that if we choose any of the attacked nodes and finally come back to it after visiting all the nodes the total path length must be unique.Here if you take nodes 1 or 2 or 3 as the starting point the total length is 4.Taking one node as root we calculate the minimum attacked node farthest from it(call it node1).Now basically we have to subtract the tree diameter from the total path length as explained in the editorial.now taking node1 as the root we find the minimum attacked node farthest from it(call it node2).their distance would be the tree diameter which we are seeking for.Here i am always calling minimum attacked node as there could be many nodes which are at the same level as compared to the root.Finally the answer is the minimum of node1,node2 as the starting point can be either ends of the diameter.
This is my solution for C http://codeforces.com/contest/592/submission/13982866. It gives correct ans for the case where I get WA on my local machine. How do I debug this? Similar issues with http://codeforces.com/contest/551/submission/12304739. Any help will be appreciated.
I didn't understand last two lines of editorial for C. Could someone explain them please?
Here is my explanation.
What we need to do here is count the summation part fast. This can be done by simple observation. If minimum floor value = vmin and max = vmax, then we will observe all floor values between vmin and vmax. Now, notice that the floor values are not random as floor((T-r) / M) is linear to r(T and M are constant). That means floor values are non-increasing if we move from r = 0 to x and non-decreasing from x to 0.
So basically we get floor values like this,
vmin, vmin, vmin, vmin + 1, vmin + 1, ......, vmax, vmax, vmax, vmax
vmin for r = x and vmax for r = 0 for equation floor((T-r)/lcm).
Now, we can also count how many v values we will get if we are standing at rth remainder. i.e. given that for current r value we get v = floor((T-r)/lcm), what is the farthest point where we will also get v. If we do that we can jump directly to next floor value which is v + 1. We do that until we reach vmax. Simple loop will do with direct jumping, or we could optimize the algorithm to get the answer directly.
So in simplest analogy, we have a very long road , road is full of coins, we are given how the value of coins change along the way by a linear equation and if we are standing at coin value v, we can find the farthest point where we will also get same coins using that equation, also we can teleport to any point, then, we will directly add (farthest_point — current_point + 1) * coin_value, and then teleport to farthest_point + 1. We continue this until we count reach the end of road.
Only if everybody helped people understanding maths.
Also, if we are at start of floor value v1, then we will see a total of LCM v1 coins adjacent until we see next floor value which is v1 + 1.
If we are at r, floor value v = floor((T-r)/lcm). The farthest point(r_farthest) where we will find floor value v will be T — v * LCM,
so simplest program to understand
For Problem D, I know how to calculate diameter, but how to determine the diameter node with minimal index in O(n)? Can anyone show me some ideas?
You basically make one of the attacked nodes a root.From there calculate the node of maximum distance(if there are many choose the smaller of them).Taking this node as root find the node of maximum distance(again in case of ties choose the smaller of them).This will require two dfs or bfs calls and hence the time complexity is O(n).
If you have found diameter, you should have started on one end of it and finished on another. It's in case you have used 2xDFS or 2xBFS to find diameter.
Does anyone know of a bug in converting unsigned long long to double?
For problem E, I thought that only one or two writing speeds should be negative in a team, neither none nor all. Let pi = ri / wi. The one with writing speed of opposite sign should have pi between the other two pi. I calculated this by iterating over a vector of pi both positive and negative separately.
wi may be zero. Now, I proved that only one wi can be zero. I calculated number of teams for two cases ri > 0 and ri < 0 and added them separately.
I get wrong answer on test case 3. Can you people help? Did anyone have similar ideas?
I solved exactly using this. You can see my solution. http://codeforces.com/contest/592/submission/14004649
Thanks for your help. This is my AC solution using the same method http://codeforces.com/contest/592/submission/14034786
Could someone explain the proof more clearly on prob D why 2e — L is minimum answer? I understood that 2e but why we get the right answer by subtracting L?
Because we needn't return to the starting city. So we go to the farthest node(L = path for this node) at the end, and wouldn't return.
i solved E problem with different idea. i think tutorial's solution isnt good. My solution : http://codeforces.com/contest/592/submission/14004649
O(NlogN) Time Complexity. It is very interesting. I wonder who solve this problem by using same method .
Can you tell me clearly what you think?I want to know your idea.
yes i can tell you.
"ri*wj > wi*rj" we can convert this expression to "ri/wi > rj/wj". but we should care wi and wj's case (pos. or neg.) to write '<' or '>'. Let xi = ri/wi.
we should find three integers i,j,k that xi <?> xj <?> xk <?> xi (<?> means '<' or '>') then look all cases for wi, wj, wk because wi,wj,wk will change expression (i meant < or > ). Care that we look w's cases. we dont look x's cases.
-> wi|wj|wk
this case will : xi > xj > xk > xi but i cant be true. it is impossible.
this case will : xi > xj > xk > xi but i cant be true. it is impossible.
this case : xi > xj && xj < xk && xk < xi. it can be true if xi > xk > xj is true.
this case : xi < xj && xj > xk && xk < xi it can be true if xj > xi > xk is true.
first put all xi values into two groups. ('positives' and 'negatives')
you can count all numbers in case 3. (case is +,+,-) Choose three value i,j,k . i from 'positive', j from 'positive', k from 'negative' that xi > xk > xj.
you can count all numbers in case 4. (case is +,-,-) Choose three value i,j,k . i from 'positive', j from 'negative', k from 'negative' that xj > xi > xk.
in other words (for case 3) choose some value from 'positive' then choose some value from 'negative' smaller then first then choose some value from 'positive' smaller then second.
i think the solutoion is clear. i forgot to say if wi == 0.
if wi == 0. we will say xi value that wi == 0 'zero value'. we seperate theese zero values from others.
because we cant use two or three zero values. because it cant be ri/0 > rj/0.
we can use one zero values. if we use zero values in case 3 (xi > xk > xj) it will be xi. if we use zero values in case 4 (xj > xi > xk) it will be xj.
thats all :)
I don't understand difference between two solutions of mine, AC : http://codeforces.com/contest/592/submission/14034786 and WA : http://codeforces.com/contest/592/submission/14034425 or WA : http://codeforces.com/contest/592/submission/14034857. Storing the value once gives AC while computing again when required gives WA. Can you please point out some difference. Thanks in advance.
help please .... why my solution for problem D got TLE it should be 6*N
I am unable understand the first testcase of problem C.
10 2 3
When L = 1, 5 and 7 then both will into abyss.
When L = 6 both will complete race at the same time.
So we should consider four cases when there will be tie. Why are we taking only 1, 6 and 7?
By Problem D. Super M, I studied about tree diameter deeply. Thanks
Div2,E Can anybody explain properly how to find the count of pairs of (j,k) for fixed i using two pointer ? I have thought about it a lot, but still not getting the method to do it! Thanks