I failed to manage any good resource on 2-SAT that illustrates printing solution for the value of each variable.Basically, I am stuck with this problem: lighoj — 1251 — Forming the Council http://www.lightoj.com/volume_showproblem.php?problem=1251
- What I did: for each (a v b) I connected -a ->b and -b ->a. Then I run SCC and check if a and -a exist in same component.
But how can I decide value of each variable?
Thanks in advance ...











Auto comment: topic has been updated by ivplay (previous revision, new revision, compare).
So you have made 2sat on the graph. That means that for all vertexes V: V is not in the same SCC az !V. Also if V and U are in the same component then their values are the sam (they are either 0 or 1). Then you chose a random SCC and set all of its values to 1 or 0 (you can chose one of them). You start DFS from any point in that SCC. Let's call that point U. Then all vertexes in the SCC of U are the same as it (0/1). And also for any vertex in the SCC of U (let's call it V) if value of V's SCC is 1 then the value of !V (or -V as you call it) is 0. The same goes if V's SCC value is 0, then the value of !V will be 1. You do DFS while there are vertexes with no set value.
After all vertexes have their value, you will have one possible solution.
It needs to be done in reverse toposort order not randomly.
I smelt something like reverse toposort order, but could not gather enough proof! whats the secret the behind reverse toposort as an working solution! Anyway , I saw many codes where random choice for any component works fine!
I don't see how random choice could work correctly for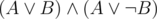 . A has to be true, but random choice could set it to false.
. A has to be true, but random choice could set it to false.
Yeah you're right, it must be in reverse topological sort order. I didn't realize that :/
As it is an implication graph , Consider a node A .
Suppose complement of A is reachable from A then A cannot be assigned the value true as that would also imply that (complement(A)) has to be true as it is reachable from A in the implication graph.
So for any pair of variables (x , complement(x)) whichever node is later in the topological ordering amongst them is assigned the value true and the other complementary one as false.
I have assumed that a valid assignment of variables exists .
Thanks to both of you
Great explanation, thanks a lot. I got the idea :)