Let's fix the number a of strings of length p and the number b of strings of length q. If a·p + b·q = n, we can build the answer by splitting the string s to a parts of the length p and b parts of the length q, in order from left to right. If we can't find any good pair a, b then the answer doesn't exist. Of course this problem can be solved in linear time, but the constraints are small, so you don't need linear solution.
Complexity: O(n2).
612B - HDD is Outdated Technology
You are given the permutation f. Let's build another permutation p in the following way: pfi = i. So the permutation p defines the number of sector by the number of fragment. The permutation p is called inverse permutation to f and denoted f - 1. Now the answer to problem is 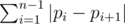 .
.
Complexity: O(n).
612C - Replace To Make Regular Bracket Sequence
If we forget about bracket kinds the string s should be RBS, otherwise the answer doesn't exist. If the answer exists each opening bracket matches to exactly one closing bracket and vice verse. Easy to see that if two matching brackets have the same kind we don't need to replace them. In other case we can change the kind of the closing bracket to the kind of the opening. So we can build some answer. Obviously the answer is minimal, because the problems for some pair of matching pairs are independent and can be solved separately.
The only technical problem is to find the matching pairs. To do that we should store the stack of opening brackets. Let's iterate from left to right in s and if the bracket is opening, we would simply add it to the stack. Now if the bracket is closing there are three cases: 1) the stack is empty; 2) at the top of the stack is the opening bracket with the same kind as the current closing; 3) the kind of the opening bracket differs from the kind of the closing bracket. In the first case answer doesn't exist, in the second case we should simply remove the opening bracket from the stack and in the third case we should remove the opening bracket from the stack and increase the answer by one.
Complexity: O(n).
612D - The Union of k-Segments
Let's create two events for each segment li is the time of the segment opening and ri is the time of the segment closing. Let's sort all events by time, if the times are equal let's sort them with priority to opening events. In C++ it can be done with sorting by standard comparator of vector<pair<int, int>> events, where each element of events is the pair with event time and event type ( - 1 for opening and + 1 for closing).
Let's iterate over events and maintain the balance. To do that we should simply decrease the balance by the value of the event type. Now if the balance value equals to k and before updating it was k - 1 then we are in the left end of some segment from the answer. If the balance equals to k - 1 and before updating it was k then we are in the right end of the segment from the answer. Let's simply add segment [left, right] to the answer. So now we have disjoint set of segments contains all satisfied points in order from left to right. Obviously it's the answer to the problem.
Complexity: O(nlogn).
612E - Square Root of Permutation
Consider some permutation q. Let's build by it the oriented graph with edges (i, qi). Easy to see (and easy to prove) that this graph is the set of disjoint cycles. Now let's see what would be with that graph when the permutation will be multiplied by itself: all the cycles of odd length would remain so (only the order of vertices will change, they will be alternated), but the cycles of even length will be split to the two cycles of the same length. So to get the square root from the permutation we should simply alternate (in reverse order) all cycles of the odd length, and group all the cycles of the same even length to pairs and merge cycles in each pair. If it's impossible to group all even cycles to pairs then the answer doesn't exist.
Complexity: O(n).
The author solution for this problem uses dynamic programming. I think that this problem can't be solved by greedy ideas. Let's calculate two dp's: z1i is the answer to the problem if all numbers less than ai are already printed, but the others are not; and z2i is the answer to the problem if all numbers less than or equal to ai are already printed, but the others are not. Let's denote dij — the least distance between i and j on the circular array and odij is the distance from i to j in clockwise order. Easy to see that z2i = minj(zj + dij) for all j such that the value aj is the least value greater than ai. Now let's calculate the value z1i. Consider all elements equals to ai (in one of them we are). If there is only one such element then z1i = z2i. Otherwise we have two alternatives: to move in clockwise or counterclockwise direction. Let we are moving in clockwise direction, the last element from which we will write out the number would be the nearest to the i element in counterclockwise direction, let's denote it u. Otherwise at last we will write out the number from the nearest to the i element in clockwise direction, let's denote it v. Now z1i = min(z2u + odiu, z2v + odvi). Easy to see that the answer to the problem is mini(z1i + dsi), over all i such that ai is the smallest value in array and s is the start position.
Additionally you should restore the answer. To do that, on my mind, the simplest way is to write the recursive realization of dp, test it carefully and then copy it to restore answer (see my code below). Of course, it's possible to restore the answer without copy-paste. For example, you can add to your dp parameter b which means it's need to restore answer or not.
Complexity: O(n2).











Can we get the editorial in english ? Please....
I'm working on it.
Thanks
Done.
It would be nice if we get the sample codes for all the problems ....
Not like there aren't hundreds of solutions to all the questions as it stands... just look at some other people's code, you'll gain a lot of new tricks you never knew about before!
For A, there's also a simple O(N) DP solution in which F[i] is true if we can represent i as A*p+B*q or false otherwise. It's easy to restore a possible sequence if F[n] is true :)
Also you can simply iterate from 0 to max_possible_B and check if ((n — i*q) mod p == 0). If found — its an answer. If not — impossible.
Hi there!
In trying on Problem E, I implemented the idea per the Editorial, to create and sort events, and linearly scan them. But I got TLE on input #19. Any ideas?
I'm not sure if it's appropriate to paste my code here. But if so, I'd love to share with you and receive any feedbacks!
You can post a link to you submission. When looking at your profile history, I see the submission history anyway.
Your I/O is too slow. There has been written a lot about
cout/cinvs.scanf/printfon Codeforces, just search.First, do not use
endlafter every line — it flushes the output buffers, therefore is slow.Second, add this code at start of
main():Then try again and it should be AC.
Totally lost in editorial of "The Union of k-Segment". what is the "balance" and what is "decrease the balance".
what is the deal with event time?in simple words please.
The algorithm being used is a Sweep line algorithm. We're sweeping the x-axis from left to right. It makes sense to call the openings and closings of the given segments 'events'. Since we want to sweep the x-axis from left to right, we're going to create a bunch of events, sort them by x-coordinate, then process them.
The balance is the number of segments that have been opened so far as I'm sweeping the x-axis. When this balance is increased to
k, you're in a satisfied part of the x-axis. When the balance decreases fromktok-1, you're on the boundary of a satisfied part of the x-axis.I am not able to understand Square Root of Permutation editorial can someone provide detailed expalnation for that ?? It will be really helpfull :)
Here are some hints: http://math.stackexchange.com/questions/266569/how-to-find-the-root-of-permutation
The answer still may be too advanced to understand if haven't studied the math of permutation groups. Basically, every permutation can be expressed in a cyclic notation. To do that, first write the permutation as multiplication of transpositions (a transposition is a cycles with two elements). For the example
q = [4, 5, 1, 2, 3], 1 maps to 4, 2 to 5 and so on, so we write it down:q = (1 4)(2 5)(3 1)(4 2)(5 3)Now some transpositions can be merged. In fact in this example all of them can be merged, but that will not always be the case:
q = (1 4 2)(2 5)(3 1)(5 3) = (1 4 2 5)(3 1)(5 3) = (1 4 2 5 3)(3 1) = (1 4 2 5 3)The resulting cycle of length 5 denotes the same original permutation
q, just in a different way.Now if
q=(i1, i2, i3, i4, i5)then inq^2elementi2moves one step away fromi1:q^2=(i1, ..., i2, ...), elementi3one step away fromi2and so on (modulo the size of the permutation):q^2=(i1, i4, i2, i5, i3)In the example,
q^2 = (1 4 2 5 3)^2 = (1 2 3 4 5). Written back in the original form, it is the permutationp = [2 3 4 5 1].The analysis so far works for cycles with odd length. For a cycle with even length
l, for examplep = (i1, i2, i3, i4)elementi_n-2maps back toi1and so on; the result in this case is two cycles with lengthl/2:p = (i1 i3)(i2 i4)To solve the exercise, you need to do the opposite: permute every odd-sized cycle back, and merge every pair of same-sized even cycles. (If there are more than one pair of cycles with size
2n, then multiple solutions exist.) If there are even-sized cycles with no pair, then a solution does not exist.Finding the cycles in the given permutation requires some preprocessing, but it can be done in
O(n)time.thank you.
It seems that while explaining how to find the square of a permutation, you have explained how to find the root of the permutation.
Link to editorial(tutorial) added under contest material on contest page is not working(redirecting to edit blog link).
D getting TLE for O(NlogN) in python.
Python isn't really a good choice for competitive programming. Some simple algorithms works there like 40 times slower than C#/Java/C++.
On top of than you should have very fast console i/o. It could be impossible to solve this task in Python at all.
You are right. I just wanted to know if anyone got AC for that problem in python.
Question to people who solved problem E in round what made you think of this problem as a graph problem? and what lead you to that observation i mean i've been to solve graph problems for a while and still i can't reach that graph mentality which enables me to realize the point of such a problem if anyone would kindly share their experience or a few pointers that would be great (p.s: sorry for double post but first time was by mistake in russian)
It is quite standart idea to consider a permutation graph. And in this problem some outputs for small cases helped me to get the right idea;)
Can you please provide some links to tutorials or problems , where this idea has been used .
I don't know about articles on English about it, you may take a look at Wikipedia though or try to find some other information in Google. There had been some problems on Codeforces with such idea but i could not find them now. One of the famous problems is to find the k-th power of the given permutation of size n. It can be solved with O(n log k) complexity using binary exponentiation but with idea of the permutation graph it can be done in O(n).
It seems to me that the solution for F is a bit incorrect. Especially, recalculating of z1. It is claimed that we need to move only in one direction (i.e. clockwise or counterclockwise). However, sometimes we need to move in one direction, then return to the initial point and continue moving in the direction, opposite to the initial direction. For example, test:
We need to do the following sequence of steps: +0, -1, +2 (or -1, +1, +1) firstly. And the suggested author's solution gives correct answer to this test. Can you please explain, what's going on?
I know it's been three years, but I also stumbled on this, so maybe it will help future upsolvers.
If you define $$$z1_i$$$ as the minimal cost of starting at position $$$i$$$ and visiting all positions with values greater than or equal to $$$a_i$$$, then indeed you have to consider a general case: move in one direction to some $$$j$$$, then move in other direction to some $$$k$$$:
In the picture above going only in one direction from $$$i$$$ will give too big cost $$$z1_i$$$. But note that cost $$$z1_j$$$ will be calculated correctly.
Now consider calculating $$$z2_x = \min_y(z1_y + d_{xy})$$$ for some position $$$x$$$ where $$$a_x$$$ is the biggest value smaller than $$$a_i$$$. If it's optimal to move from $$$x$$$ to $$$i$$$ (i.e. $$$y=i$$$ achieves minimum), then we make a move from $$$x$$$ to $$$i$$$ and then to $$$j$$$. Since all values $$$a_i$$$ will be visited on path from $$$j$$$ to $$$k$$$, we could have moved directly from $$$x$$$ to $$$j$$$. Thus $$$y=j$$$ also achieves minimum, and since $$$z1_j$$$ is correct, then $$$z2_x$$$ will also be correct.
To summarize: values $$$z1_i$$$ in author's solution are sometimes bigger than advertised, but it doesn't matter, since there is at least one correct value that achieves minimum.
Question about 612E: I didn't get what the editorial means with merge cycles in each pair. For example, the permutation
2 1 4 3has two cycle of size 2 which are2->1->2and4->3->4. How should I merge this?I ran one correct solution for this input and I got
3 4 2 1which means that the result of merge should be3->2->4->1->3. But I didn't get the idea behind the merge process.See my answer to masterwayne
Can someone explain me why C problem 11-th test answer is 7? Input:
(([{>}{[{[)]]>>]
My program outputs 3 and I when I tried to do this manually I also found that only 3 changes are needed:
(([{>}{[{[)]]>>]
'<'([{>}'<'['<'[)]]>>]
Did I misunderstand the problem or the test is wrong?
Why in Problem D. The Union of k-Segments in first sample test with input:
we get output
and not
as far as I can see all the points of interval 0 5 belongs to at at least 2 segments therefore set of one segment (0 5) is the smallest?
Actually it's not. Here the problem says that all satisfied points (I presume that you are mistaking for satisfied INTEGER points) must be included. Indeed, 2 and 3 are satisfied points but 2.5 is not
you can solve problem A using dp in linear time 167881923
For the future solvers
Problem D
test#1 case ans is two segments because all the real numbers between 2 and 3 aren't satisfying the condition
test#2 case all the real numbers between 2 and 3 also satisfying the condition so only one interval is required
My appraoch
since real numbers check is required so our standard sweep line template wont work, we need to add some more checks, the way i did it quite easy to understand i think,
lets say our current interval is [ a , b ] and previous valid interval is [ c , d ] if these points are integer then can't have the information of the numbers in between two intervals so we need real numbers, but that will not be very intuitive when implementing.
so what i did is, multiplied each interval end point by 100,
and updated the map, mp[left]++ , mp[right+1]--;
now if two intervals differ less than 2 then they can be merged if not they will be seperated,
this above implementation is same as having real number of precision of 0.01, but we are doing it with integers only.
here is the my AC code implementation: