→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/27/2024 02:15:04 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










the content isn't working now: while opening file this message is found "the archive is either in unknown format or damaged"
Very strange. Anybody has a similar problem?
Yes, me too.
I had that problem too. But when I opened that file with 7zip, it has been opened normally.
Does anyone know how to solve 3rd problem (C problem) in better complexity than O(N*sqrt(N))?
Consider a set of points (l, r) on plane such that 0 ≤ l ≤ r ≤ n - 1 where the point (l, r) corresponds to a segment [l, r].
Consider some number x and all its occurrences. Suppose that the number x is one of the numbers that make some particular segment [l, r] be bad. Then one of the following situations should happen: either there are from 1 to x - 1 or more than x + 1 occurrences of x in [l, r]. That means that for the fixed l there are two segments of banned values for r. Actually, for any possible l lying between two consectuvie x's, those two banned segments for r will be the same. It can be reformulated that there are O(cx) banned rectangles on a plane that point (l, r) isn't allowed to be in, where cx is the number of occurrences of x.
Construct all such rectangles for all numbers x, there will be O(n) of them in total, and then calculate the number of points that do not lie in any banned rectangle in via sweeping line.
via sweeping line.
Although this solution has better time complexity, there are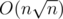 solutions that work even faster because they do not utilize much memory and use only simple operations.
solutions that work even faster because they do not utilize much memory and use only simple operations.
Code for reference:
Sorry, just mixed up.
Why it's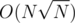 ?
?
Isn't there supposed to be an extra line between 26 and 27 which is like line 31?
Ask not me, but Errichto.
But you are good enough to check other's code right?
nah, I'm more about writing comments :)
:)) thanks for not helping :))
.
Can someone explain the solution of problem A Day1?
The download link doesn't work for me, can you share the problem statements somewhere else?
It's in Russian anyway
Oh ok. I thought it was in english since the discussion was in english.
Problem A
GL & HF :)