It's optimal to do the biggest possible step everytime. So elephant should do several steps by distance 5 and one or zero step by smaller distance. Answer equals to 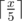
Solution 15550796
We are given array which contains only ones and zeroes. We must divide it on parts with only one 1.
Tricky case: when array contains only zeroes answer equals to 0.
In general. Between two adjacent ones we must have only one separation. So, answer equals to product of values posi - posi - 1 where posi is position of i-th one.
Bonus: what's the maximal possible answer for n < 100?
Solution 15550806
First radius equals to zero or distance from first fountain to some flower. Let's iterate over this numbers. Second radius equals to maximal distance from second fountain to flower which doesn't belong to circle with first radius. Now we should choose variant with minimal r12 + r22.
Bonus: It's O(n2) solution. Can you solve problem in O(nlogn)?
Solution O(n2) 15550812
Solution O(nlogn) 15550822
Answer equals to one if all coordinates x or y of points are same.
When answer equals to two? Let's iterate over all pairs of points. Let first point in pair is beginning of polyline, second point is end. Only one or two such polylines with answer two exist. If third point is on the polyline it belongs to rectangle with corners in first two points. We can just check it.
Else answer equals to three. We can build vertical lines which contains the most left and the most right point and horizontal line through third point. If we erase some excess rays we will get polyline.
Solution 15550843
617E - XOR and Favorite Number
We have array a.
Let's calculate array pref (pref[0] = 0, 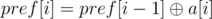 ).
).
Xor of subarray a[l...r] equals to 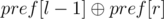 .
.
So query (l, r) is counting number of pairs i, j (l - 1 ≤ i < j ≤ r) 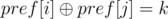 .
.
Let we know answer for query (l, r) and know for all v cnt[v] — count of v in a[l - 1...r]. We can update in O(1) answer and cnt if we move left or right border of query on 1. So we can solve problem offline in 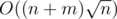 with sqrt-decomposion (Mo's algorithm).
with sqrt-decomposion (Mo's algorithm).
Solution 15550846










Bonus in C — ternary search on first radius?
http://codeforces.com/contest/617/submission/15538579
Ternary Search won't work. I tried the same during contest and after it.
What I had assumed was that the
sum = r1^2 + r2^2will first decrease as we increaser1from zero and then increase after a certain "sweet spot". Turns out, that assumption was wrong.An example for that is say we have fountains at
(0, 0)and(10, 0)and a flower at(0, 15). Nowsumincreases asr1increases from zero, sincer1is increasing butr2remains the same since it has to cover point(0, 15)till the timer1can't cover it.For problem D, did anyone else interpret
To mean that the kind of shape on the left would be invalid and that you would need at least three segments (like on the right) for the following example?
Because personally, a few of my fellow competitors and I found it very confusing which led to me being hacked and not knowing why.
Sorry for potato quality, let me know if you guys had the same issue.
Edit: These are the six valid line configurations that yield an answer of
2.That is self touching like you suspected. Did you consider the case where the x-value of the bottom point lies outside of the x-range of the other two points?
Shape on the left is invalid because it isn't polyline
Yes it's the same here, I thought that the answer for the left case is (2) !
During last 3 minutes of the contest the server was very lag. Luckily I could submit again my solution for D at that time and got AC after the system testing. Anyway, this contest was very tricky and interesting :)
Bonus C: use set to store points, that are currently belong to second circle, sorted by distance to the centre of the second circle (from the farthest to the nearest). Sort all points by their distance to the centre of the first circle (from the nearest to the farthest). Now iterate over this points: you should erase current point from set and try to update your answer (it will be min(ans, dist(*st.begin(), r2) + dist(a[i], r1)).
Yes, you're right.
I don't think I understand your explanation.
Are you saying to map each point to the circle which is closest to it? Some form of greedy approach?
Ehmm, not really. You should just keep two sets of points, which belongs to appropriate circle. This can be done by storing one set of points in std::set and another set of points in a sorted vector.
Here's my code: http://pastebin.com/wT5t0etA
P.S. Sorry for my poor english ;(
nlogn solution for C. http://codeforces.com/contest/617/submission/15538579
Store the distances of each flower from fountain1 in a vector. Sort this vector, let D1. It stores the prospective values of R1. Store the maximum values of Suffixes of distances of flowers from Fountain2. Now iterating over the distances in D1 vector, it is easy to see that if R1 is equal to D1[i], it means that Fountain1 can cover all of 0..i flowers. So now we need the value of R2 needed to water flowers i+1...n-1. R2 is the max distance of any of these flowers from F2. (obtained from the suffix maximum we stored earlier)
WOW! Very nice solution
Most welcome, Ayush :P
Bonus B: 3*2^48
Would someone mind clarifying, in O(n2) solution to C, what the significance of the line
dist.push_back({0, 0})is? It is required for AC.Case if radius of one of fountains equal to zero
B can be also solved using DP with state f[i] representing cuts ending at position i. Solution 15522284
I solved C in nlogn ! my solution is like this , for every point store two distances , distances1 from fountain1 and distance2 from fountain2 . sort the points on basis of distance1 in decreasing order and now for every i do this solution=min(solution,distance1[i]+maxvalue_of_distance2_upto_i)
How to solve E in O(n*polylog)?
I know how to reduce my problem to counting cnt[v] * cnt[v] but don't know what to do next.
Let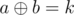 .
. 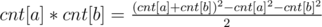
We can consider following:
So we have two arrays ai and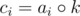 . We need to count number of l ≤ i, j ≤ r such that
. We need to count number of l ≤ i, j ≤ r such that 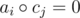 , i.e. ai = cj. Any ideas what to do with it?
, i.e. ai = cj. Any ideas what to do with it?
Anybody did n^2 dp for problem B?
for problem D: in the following case,Why shouldn't the answer be 2 ?
A B -----.-----. | | . CCould someone explain Problem — E ? The editorial is not easy to understand.
In the editorial, prefix[i] = prefix[i — 1] ^ A[i] (^ means xor) and cnt[v] = number of elements with prefix[i] = v, where i lies in the current mo's windows. So now, in mo's algorithm, you push the queries in sqrt(N) blocks according to left pointer, and then sort each block of queries according to right pointer. Now when you add an element to the window, suppose element A[x] is inserted in the window, where x is the indice added and y = prefix[x] ^ k, then ans += (cnt[y]). We do this because cnt[y] stores all the elements in the current window having prefix xor equal to y. And if we do xor of prefix[x] with any of these elements then the resultant xor will be k. While adding and removing you also need to constantly update cnt[] array.
See the editorial code for a clearer view.
Thanks :)
Can someone explain problem D? I had a look at the solution and cannot understand what's the need of the function is_between()? 617D - Polyline
Given three points you have to find whether any three points satisfy the properties as given.Here's how to solve . Three conditions have to be considered:
All points are collinear , answer is 1 (All points are in a straight line) .
All points are not collinear , answer is 3 :) .
Only two points lie in a same axis , This is the case we have to think about :
i> If all points form a pythogorean triplet , answer is 2 .
ii> If axes( Either X or Y coordinate ) of a two point are equal , we check whether the other third point come strictly bellow or above the other pair. In this case the answer is 2 . Else if it comes between the two points , the answer is 3 .
In the 3rd point : - There is no need to check for the pythogorean triplet. Only checking if the third point lies strictly below or above the other pair or if it lies in between the points is enough. I got it accepted without checking for a pythogorean triplet
for problem C we can also make a binary search on the answer here is my code : 15552813
why do we have to use the pref[i] = pref[i-1]^a[i]; instead of just testing with the normal number?
Because we are interested in number of subarrays such that A[i]^A[i+1]..A[j-1]^A[j] is equal to k. A[i]^A[i+1]..A[j-1]^A[j] = pre[j]^pre[i-1]
Could someone explain the following case for the problem 617D — Polyline:
(1, 1)(2, 2)(3, 3).Aren't we need 4 segments to construct the polyline?
No answer is 3 . with these points : (3,3)->(3,2)->(1,2)->(1,1)
No, correct answer: 3 segments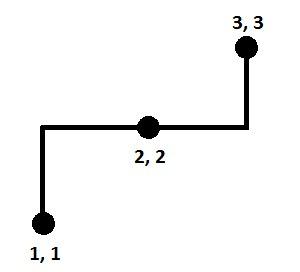
Wow, that configuration didn't come to my mind :)
Thank you.
Can anyone make me understand this line written in problem E?
Let we know answer for query (l, r) and know for all v cnt[v] — count of v in a[l - 1...r]. We can update in O(1) answer and cnt if we move left or right border of query on 1. So we can solve problem offline in with sqrt-decomposion (Mo's algorithm).
Same doubt ..did you get it later?
Nope AJBOI..
in problem E(xor and favourite number),what does cnt[v] of the following line mean: "Let we know answer for query (l, r) and know for all v cnt[v] — count of v in a[l - 1...r]. "