Div 2. Problem А. Cifera
To solve this task, let's describe what is needed more formally. We should answer whether is number l some positive degree of number k or no. To answer this question we can proceed in 2 ways:
1) Using 64 bit data type, we can find minimal degree h of number k, such that kh ≥ l. If kh = l, then the answer is YES, and number of articles is equal to h - 1. Otherwise, the answer is NO.
2) We will divide l by k, until k divides l and l ≠ 1. If l = 1, then the answer - YES and number of articles is equal to numberOfDivisions - 1, and the answer is NO otherwise.
1) Using 64 bit data type, we can find minimal degree h of number k, such that kh ≥ l. If kh = l, then the answer is YES, and number of articles is equal to h - 1. Otherwise, the answer is NO.
2) We will divide l by k, until k divides l and l ≠ 1. If l = 1, then the answer - YES and number of articles is equal to numberOfDivisions - 1, and the answer is NO otherwise.
Div 2. Problem B. PFAST Inc.
We can reformulate the statement more formally.
In this case, we have a undirected graph, and we have to find some maximal clique in it. If we have a look to constraint n ≤ 16, then there can be noticed that we can iterate over all possbile subsets of vertices and find the answer. To do this, one can use bit masks and iterate from 0 to 216, checking current subgraph for being a clique. Also, it's necessary not to forget about sorting the names while printing the answer.
In this case, we have a undirected graph, and we have to find some maximal clique in it. If we have a look to constraint n ≤ 16, then there can be noticed that we can iterate over all possbile subsets of vertices and find the answer. To do this, one can use bit masks and iterate from 0 to 216, checking current subgraph for being a clique. Also, it's necessary not to forget about sorting the names while printing the answer.
Div 1. Problem A. Grammar Lessons
This task is an example of task that requires accurate realization.
After reading the statement one can understand that we have to check whether the text from input represents exactly one correct sentence or no. If yes, therefore the text can be either a single word from our language or a following structure:
{zero or non-zero count of adjectives} -> {a single noun} -> {zero or non-zero count of verbs}, and moreover, all these words should have equal gender.
So, to check these facts, one can do the following:
We count number of words. If this number is equal to 1, we check this word for being a valid word from our language. Otherwise, we can get gender of the first word, and iterate through the rest of the words validating existing of only one noun and order of these words. Also, while iterating we check the gender of each word for being equal to the gender of the first word.
Div 1. Problem B. Petr#
Let's find all occurrences of begin and end. Then we'll map the whole string to number 0. After this we will simply add one symbol per iteration to already seen sub-strings and map new strings to some non-negative integers. One can notice that we will never reach a situation when more then 2000 different strings exist, so we can map them easily. Now, as per we know all the ends and beginnings of strings and different string of equal length are mapped to different numbers ( and equal strings are mapped equally), we can simply count the number of necessary sub-strings of certain length. So, we have time complexity O(N2LogN), since we are making N iterations and each is done in O(NLogN) time.
Div. 1. Problem C. Double Happiness
In this task one have to find quantity of prime numbers that can be reproduced as sum of two perfect squares. Obviously, that 4k + 3 prime numbers are not suitable as sum of two perfect squares can not be equal to 3 (of course, modulo 4). So, we can prove or use the well-known fact ( also known as Fermat theorem), that every odd 4k + 1 prime number is a sum of two perfect squares. Also, we have not to forget about 2, as 2 = 12 + 12.
Now, how can we get this task accepted? Simply using the sieve will exceed memory limit, but we can use block sieve, that works in the same time (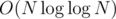 ), but uses
), but uses 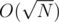 of memory. Also, we can use precalc for intervals of length equal to 100000. Also, Romka used the fact, that using bitset compress memory up to 8 times, and it will enough to suite the ML. Also, it would be nice to count only odd numbers while buliding the sieve.
of memory. Also, we can use precalc for intervals of length equal to 100000. Also, Romka used the fact, that using bitset compress memory up to 8 times, and it will enough to suite the ML. Also, it would be nice to count only odd numbers while buliding the sieve.
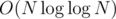 ), but uses
), but uses 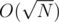 of memory. Also, we can use precalc for intervals of length equal to 100000. Also, Romka used the fact, that using bitset compress memory up to 8 times, and it will enough to suite the ML. Also, it would be nice to count only odd numbers while buliding the sieve.
of memory. Also, we can use precalc for intervals of length equal to 100000. Also, Romka used the fact, that using bitset compress memory up to 8 times, and it will enough to suite the ML. Also, it would be nice to count only odd numbers while buliding the sieve.Div. 1. Problem D. Museum
Let's consider a pair (i, j) as a state - this means that now Petya is in room i, and Vasya is in room j. Therefore, their meeting is state (i, i) for some i. So, it's quite easy to build transition matrix - this means that for each state (i, j) we will know probability of reaching state (x, y) in one step, where 1 ≤ i, j, x, y ≤ n. Also, from meeting state we can reach only the same state.
Let's try to solve such a problem - what is the probability of meeting in the first room? We build system of linear algebraic equations:
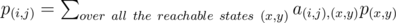 , where a(i, j), (x, y) — probability of transition from state (i,j) to state (x,y). One can notice that p(1, 1) = 1, and p(i, i) = 0 when i ≠ 1, and the answer will be p(a, b).
, where a(i, j), (x, y) — probability of transition from state (i,j) to state (x,y). One can notice that p(1, 1) = 1, and p(i, i) = 0 when i ≠ 1, and the answer will be p(a, b).
This system can be easily solved using Gauss method. Similarly we can solve such a problem for every room (considering that we will meet in certain room), but we have complexity O(n7), that will not pass time limit. But, after some observations, we now see that each time we are solving system Ax = b (and the only thing that is changing — is vector b). So, we can solve matrix equation Ax = b, where b is a matrix with dimensions n2 * n, and the answer will be in the row that corresponds to state (a, b) . With this approach we have time complexity O(n6), that will pass time limit.
Let's try to solve such a problem - what is the probability of meeting in the first room? We build system of linear algebraic equations:
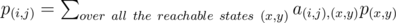 , where a(i, j), (x, y) — probability of transition from state (i,j) to state (x,y). One can notice that p(1, 1) = 1, and p(i, i) = 0 when i ≠ 1, and the answer will be p(a, b).
, where a(i, j), (x, y) — probability of transition from state (i,j) to state (x,y). One can notice that p(1, 1) = 1, and p(i, i) = 0 when i ≠ 1, and the answer will be p(a, b).This system can be easily solved using Gauss method. Similarly we can solve such a problem for every room (considering that we will meet in certain room), but we have complexity O(n7), that will not pass time limit. But, after some observations, we now see that each time we are solving system Ax = b (and the only thing that is changing — is vector b). So, we can solve matrix equation Ax = b, where b is a matrix with dimensions n2 * n, and the answer will be in the row that corresponds to state (a, b) . With this approach we have time complexity O(n6), that will pass time limit.
Div. 1. Problem E. Sleeping
Let's consider function F(x) (where x is some moment of time) — amount of moments from 0..00:00..00 up to x (and x doesn't switch to next moment ) when n k or more digits will be changed . The answer will be F(h2: m2) - F(h1: m1), also it's necessary not to forget that if h2: m2 < h1: m1, then F(h2: m2) will be enlarged by a day.
Now we will learn how to calculate F(x). To start with, let's count amount of such numbers when hour will remain the same. As hour is not changing, then k or more digits have to be changed in minutes, but in this case we need our number of minutes to be of the following form:
a..a99...9, where a means any digit,and at the end we have k - 1 nines. So k digits are changing every moment that is divisible by 10k - 1.
So, the total amount of such moments (without changing an hour) is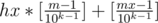 , wherehx и mx are numbers of hour and minute in time moment x, and [] is integer part.
, wherehx и mx are numbers of hour and minute in time moment x, and [] is integer part.
Now let's deal with such moments when hour is changing. If this happens, then minute turns from m - 1 to 0, and we have y different digits, where y is amount of non-zero digits of number m - 1. Therefore we have to count for hours ( in similar way) amount of moments, when k - y or more digits will be changed. k - y digits are changing every moment that is divisible by 10max(0, k - y - 1), this means that total amount of such moments is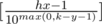 . And the final value of F is
. And the final value of F is 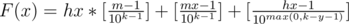 .
.
Now we will learn how to calculate F(x). To start with, let's count amount of such numbers when hour will remain the same. As hour is not changing, then k or more digits have to be changed in minutes, but in this case we need our number of minutes to be of the following form:
a..a99...9, where a means any digit,and at the end we have k - 1 nines. So k digits are changing every moment that is divisible by 10k - 1.
So, the total amount of such moments (without changing an hour) is
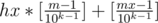 , wherehx и mx are numbers of hour and minute in time moment x, and [] is integer part.
, wherehx и mx are numbers of hour and minute in time moment x, and [] is integer part.Now let's deal with such moments when hour is changing. If this happens, then minute turns from m - 1 to 0, and we have y different digits, where y is amount of non-zero digits of number m - 1. Therefore we have to count for hours ( in similar way) amount of moments, when k - y or more digits will be changed. k - y digits are changing every moment that is divisible by 10max(0, k - y - 1), this means that total amount of such moments is
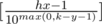 . And the final value of F is
. And the final value of F is 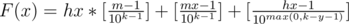 .
.










is it possible to solve it greedy ??!
i mean ..
1.clear the person that doesn't get on well with the max number of people
if there still some one doesn't get on well with another
repeat 1
else
print the ans
__
is that okay?!
in your case b is the person that doesn't get on well with the max number of people (a and c)
then first remove b
that gives a and c with no problems
then the ans is 2 a c
5 4
a
b
c
d
e
a d
a e
b d
c e
----
the answer is 3 a, b, c . but it's not achievable using greedy.
and connect every pair of vertices that are diametrically opposed.
The biggest clique is of size two, and all degrees are 3.
Add a triangle.
The biggest clique is now the triangle, but the first three vertices removed would be those of the triangle.
update: Here is a corresponding testcase. The answer is "g h i".
9 24
a
b
c
d
e
f
g
h
i
a c
a e
c e
b d
b f
d f
a g
a h
a i
b g
b h
b i
c g
c h
c i
d g
d h
d i
e g
e h
e i
f g
f h
f i
Anyone has a reference for an explanation of this algorithm?
choosing from between them randomly ...(first to find or last , depends on ur Algorithm) won't give the right answer for all the cases ...
Suffix tree/array seems to be most efficient way to solve B.
Thanks. good editorial
In problem E, the formula of $$$F(x)$$$ should be
Yes, there is some problem with border processing.
can anybody provide code for Div 1. Problem B. Petr# using editorial approach. i'm getting MLE :(
:) can u help me pls, i got wa on test 24
I looked at your submission but couldn't understand it (sorry!) but i can tell you what i did.
I simply store all indices (start) of s which begin with s_beg and all indices (end) that end with s_end. then for each pair of start,end i store hash of substring to ensure no substring is counted more than once. 222393498
I hope it helps :)
thanks