651A - Joysticks
Idea author: fcspartakm, preparation: fcspartakm.
Main idea is that each second we need to charge the joystick with lowest power level. We can just emulate it or get an O(1) formula, because process is very simple.
651B - Beautiful Paintings
Idea author: fcspartakm, preparation: fcspartakm.
Lets look at the optimal answer. It will contain several segment of increasing beauty and between them there will be drops in the beautifulness. Solution is greedy. Lets sort all paintings and lets select which of them will be in the first increasing segment. We just go from left to right and select only one painting from each group of several paintings with the fixed beauty value. We continue this operation while there is at least one painting left.
With the careful implementation we will get  solution.
solution.
But this solution gives us the whole sequence, but the problem was a little bit easier — to determine number of such segments. From the way we construct answer it is easy to see that the number of segments always equal to the maximal number of copies of one value. Obviously we can't get less segments than that and our algorithm gives us exactly this number. This solution is O(n).
651C - Watchmen/650A - Watchmen
Idea author: ipavlov, preparation: ipavlov.
When Manhattan distance equals to Euclidean distance?
deu2 = (x1 - x2)2 + (y1 - y2)2
dmh2 = (|x1 - x2| + |y1 - y2|)2 = (x1 - x2)2 + 2|x1 - x2||y1 - y2| + (y1 - y2)2
So it is true only when x1 = x2 or y1 = y2. This means that to count the number of such pair we need to calculate number of points on each horizontal line and each vertical line. We can do that easily with the use of std::map/TreeMap/HashMap/Dictionary, or just by sorting all coordinates.
If we have k points on one horizontal or vertical line they will add k(k - 1) / 2 pairs to the result. But if we have several points in one place we will count their pairs twice, so we need to subtract from answer number of pairs of identical points which we can calculate with the same formula and using the same method of finding equal values as before.
If we use TreeMap/sort then solution will run in  and if unordered_map/HashMap then in O(n).
and if unordered_map/HashMap then in O(n).
651D - Image Preview/650B - Image Preview
Idea author: fcspartakm, preparation: fcspartakm.
What photos we will see in the end? Some number from the beginning of the gallery and some from the end. There are 4 cases:
- We always go right.
- We always go left.
- We initially go right, then reverse direction, go through all visited photos and continue going left.
- We initially go left, then reverse direction, go through all visited photos and continue going right.
First two cases are straightforward, we can just emulate them. Third and fourth cases can be done with the method of two pointers. Note that if we see one more picture to the right, we spend more time on the right side and the number of photos seen to the left will decrease.
This solution will run in O(n).
Alternative solution is to fix how many photos we've seen to the right and search how many we can see to the left with binary search. For this method we will need to precompute times of seeing k pictures to the right and to the left. But this is solution is  , which is slightly worse then previous one, but maybe it is easier for somebody.
, which is slightly worse then previous one, but maybe it is easier for somebody.
651E - Table Compression/650C - Table Compression
Idea author: LHiC, preparation: iskhakovt.
First we will solve our problem when all values are different. We will construct a graph, where vertices are cells (i, j) and there is an edge between two of them if we know that one is strictly less then the other and this relation should be preserved. This graph obviously has no cycles, so we can calculate answer as dynamic programming on the vertices:
for ( (u, v) : Edges) {
dp[v] = max(dp[v], dp[u] + 1);
}
We can do this with topological sort or with lazy computations.
But if we will construct our graph naively then it will contain O(nm(n + m)) edges. To reduce this number we will sort each row and column and add edges only between neighbours in the sorted order. Now we have O(nm) edges and we compute them in 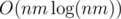 time.
time.
But to solve the problem completely in the beginning we need to compress all equal values which are in the same rows and columns. We can construct second graph with edges between equal cells in the same way as before and find all connected components in it. They will be our new vertices for the first graph.
650D - Zip-line
Idea author: LHiC, preparation: LHiC.
We need to find the longest increasing subsequence (LIS) after each change if all changes are independent.
First lets calculate LIS for the initial array and denote its length as k. While calculating it we will store some additional information: lenl[i] — maximal length of LIS ending on this element. Also we will need lenr[i] — maximal length of LIS starting from this element (we can calc it when searching longest decreasing sequence on reversed array).
Lets solve the case when we take our new element in the resulting LIS. Then we just calculate maxi < a, h[i] < b(lenl[i]) + 1 + maxj > a, h[j] > b(lenr[j]). It can be done online with persistent segment tree or offline with scanline with regular segment tree in  time. This is the only case when answer can be larger then k, and it can be only k + 1 to be exact. Second case is when we change our element and ruin all LIS of size k. Then answer is k - 1. Otherwise we will have at least one not ruined LIS of size k and it is the answer.
time. This is the only case when answer can be larger then k, and it can be only k + 1 to be exact. Second case is when we change our element and ruin all LIS of size k. Then answer is k - 1. Otherwise we will have at least one not ruined LIS of size k and it is the answer.
Lets calculate number of different LIS by some modulo. It can be done with the same dynamic programming with segment tree as just finding LIS. Then we can check if liscount = liscountleft[a] * liscountright[a]. This exactly means that all sequences go through our element.
But if you don't want the solution with such "hashing" there is another approach. For each element we can calc if it can be in LIS. If so then we know on which position it will go (lenl[i]). Then for each position we will know if there are several elements wanting to go on that position or only one. If only one then it means that all LIS are going through that element.
Overall complexity is  .
.
P.S. We can solve this without segment tree, just using alternative approach to calculating LIS with dynamic programming and binary search.
650E - Clockwork Bomb
Idea author: Zlobober, preparation: Zlobober.
First idea is that answer is always equals to the number of edges from the first tree, which are not in the second one. This means that if we have an edge in both trees we will never touch it. So if we have such edge we can remove this edge and merge its two vertices together, nothing will change.
Second idea that if we will take any edge from the first tree there always exists some edge from the second tree, which we can swap (otherwise second graph is not connected, but the tree is always connected). So the order of adding edges from the first tree can be arbitrary.
Third idea is that if we will select leaf node in the first tree, then cut its only edge, then we can add instead of it any edge going from this vertex in the second tree.
Overall algorithm: we store linked lists of edges in vertices, when edge is in both trees we use disjoint-set union to merge vertices and join their lists. We can simply traverse first tree to get any order of edges in which the current edge will always contain leaf as one of its vertices.
Complexity is O(nα), which in practice is almost linear.










Finally...
16609675
What does this above solution for the Div2-C run in? Is it O(nlogn) or O(n) or worse than that? I'm not able to figure out. Thanks!
nlgn because you sort the array of guards
maybe even worse than nlog n, because you have two nested for loops in the end, but I couldn't determinate what the exact complxcity...
Good contest.
There is no point in sorting an array in div2B. Number of segments with increasing beauty is just the maximal number of occurences of the same beauty (denote it by X). It cannot be less, because there is at most one painting with the most frequent beauty in each segment, and we can make it exactly X with a greedy algorithm. So we lose at least (X-1) happinesses on the borders of these segments of (N-1) possible, the answer is (N - 1) - (X - 1) = N - X, and we can get it in O(n) time.
Yes, i've described the solution for the harder problem — how to output this sequence.
Awesome. Took some time to understand well.
The idea is awesome once you understand it. Maybe a more detailed description will be better? When I was trying to follow the idea, I was confused by this test case: 100 100 100 100. Once you can figure out how this test case follows the idea described above, you will understand it.
It is always hard to determine what details to explain and what to omit (in explanation of an algorithm or mathematical proof), because different people need different degree of detalization.
romanandreev can you please give the c++ code of problem C- watchmen using TreeMap/sort
When i say A/B/C, i mean A or B or C.
Hello.
Could anyone please explain in C how we get 11 in the second output?
0 0 0 1 0 2 0 1
4*(4-1)/2 — 2 = 4
0 1 -1 1 0 1 1 1
4*(4-1)/2 — 2 = 4
4 + 4 = 8
Where am I wrong?
Hello, if I can see well, then second input is:
61) 0 02) 0 13) 0 24) -1 15) 0 16) 1 1Now, let's see.. for first point it is true while paired with points2 3 5, for second3 4 5 6for third5for fourth5 6and for fifth6(notice I have not wrote the duplicates) anyway it makes3+4+1+2+1+0==11.can anyone explain the implementation of div2-c problem??
Hello, well .. it is true for pair of points if they share x or y coordinate. So an implementation would look like to group all points, which share x/y coordinate. It can be done by two maps, which would be indexed by the coordinate. Here, for every group, the number of pairs is N*(N-1)/2. Anyway here is a little problem, that all pair points which share both x/y coordinate (so they are same) were counted twice. So you will have to create another map, indexed by the points (and every group will be substracted by similar formula [N*(N-1)/2])
Thanks for editorial! I have one issue for future editorials in general — difficulty in problems like DIV2-A and DIV2-B lies mostly in proving the greedy algorithm correctness, not in implementation, so it would be really nice if future editorials focus a little bit more on how to prove such greedy solutions. I understand writing full proof might be tiresome thing to do, but it gives a reader a really good opportunity to learn how to prove things quickly and in contest time.
I've added some explanation to the DIV2B problem. But i think tutorials should leave reader something to think about. Also some things are omitted for the sake of simplicity.
Could someone please explain Div2 E in more detail? Especially this part "But to solve the problem completely in the beginning we need to compress all equal values which are in the same rows and columns. We can construct second graph with edges between equal cells in the same way as before and find all connected components in it. They will be our new vertices for the first graph."
That is: Split the table in two graphs, first graph contains the vertices having unique value, and the second graph contains other vertices. For the second graph, add edges between same cells, and 'shrink' them(using dsu), these new vertices will be added to the first graph. Finally, we can get the min value of each cell through the toposort on the first graph.
Therefore, 3 steps in total: 'shrink' equal cells, add one-way edges, do toposort.
I think there is another solution for DIV1C with union-find sets and greedy.
Describe it, please! :D
Sort the whole array and then iterate it from smaller to larger. Maintain the maximum value of every row and column to decide what the next value will be.
I tried using this method only, but we have to take care that if a number occurs multiple times in a row or a column, then its final value should also be same. And a number x if it occurs multiple times but in different row and column then its final value needn't be same. How to handle this?
Use union-find sets to merge the sets of every "relevant" element, whose values should be the same. For every set you iterate all its members and get the maximum of their rows and columns.
prateek_jhunjhunwala The way to handle the case of equal values would be to make use of Disjoint set data structure to make sure that all the equal values which need to be SAME are put together in a single set.
You can read this here 18008861.
From lines 33 to 45 you can see the application of disjoint set to put equal values together. And in line 44
f[r2] = max(f[r1],max(f[r2],max(ax[a[k].x],ay[a[k].y])) ) ;
You can see that the parent has the best possible value that needs to be set for all the EQUAL values in this set. Finally in line 48
ans[a[k].id] = max( f[find(a[k].x) ] , f[find(a[k].y) ] ) +1 ;
We set the answer.
We had such solution as main, but i've decided to describe another one, because it contains more general ideas.
Why 651E's time complexity is O(NM log(NM)) instead of O(NM(log M+log N))? I wonder if there are mistakes during my analysis. http://codingsimplifylife.blogspot.tw/2016/03/codeforces-651etable-compression.html
Don't worry, you're ok. There's a logarithm property that says:
log(a*b) = log(a) + log(b)
So, NM log(NM) = NM(log(N)+log(M))
;D
Wow, I got it!
Thanks for your explanation!
:D
(Did I ask a stupid question? Why my comment vote became so negative...)
I guess that they thought that you should know that. But we are humans :D
I have thought over it for hours still not able to find the testcase I am failing. http://codeforces.com/contest/651/problem/D http://codeforces.com/contest/651/submission/16641326
You can temporary fix that test (only temporary!) Something like
if(result == 74815) result++
So you'll pass that test (but maybe your code have another bug in the next test cases). But you need to fix that bug anyways.
This algorithm is amazing; it can solve any Codeforces problem in O(#testcases) time by reducing it to 100 if statements!
I feel a small testcase can always tell me where my algorithm is going wrong. Anyways thanks for the help.
Yes, that's right. But if you are in hurry, is a simple fix.
Just in case you still need it, here is a small test case your code fails on: 5 1 100 7 hhhhw Correct answer is 4 but your code prints 2.
Could you please explain why following test case gives 7 as answer???
10 2 3 32 hhwwhwhwwh
considering 1-indexed, shouldn't answer be 8 (1-2 && 5-10) with time 31. Need help.
Thnx
Can someone explain more about div 1 D? What does scanline mean?? I dont undrestand the approach explained in the editorial :/
In this case scanline means that we have 2D points (a, b) and we are going through them from left to right (scanning by x axis) and storing segment tree on the y-values (y-axis line).
Здравстуйте! Обьясните мне пожалуйста почему в задаче 651C — Хранители/650A — Хранители мы отнимаем только количество одинаковых точек, а не их вклад в общий ответ? Как я понимаю таким образом мы отнимаем только те пары, между которыми расстояние равно 0.
Hello! Please, explain to me why in problem 651C — Хранители/650A — Хранители we subtract only number of similar points, not their contribution to the total answer? As I understand doing this we subtract only point pairs which have distance 0.
Hello. Well if we wouldn't do it, we would get all pairs which share x coordinate + all pairs which share y coordinate. As you can see from the "statement" we clearly counted every pair, which shared both ( x and y) coordinates twice [once because they share x + once because they share y ]. So here we just substract only the pairs, we counted twice :) (which are all pairs, which are same).
Thanks a lot!
for Div1 E, i have a solution which requires union-find-delete DS implementation which i dont know how to implement. does any one has a solution which does not requires union-find-delete implementation ?
Described solution doesn't need delete operation. Read it more carefully.
In problem 651D suppose we want to find maximum number of photos we can see if we first travel right and then travel left.so basically how to know at which index we should stop when we first go right
We go through all right positions and for each one of them we identify the optimal leftmost position.
Could someone explain Div1 D(Zip line) in more detail? I don't understand exactly except the fact that answer can be k-1, k, k+1.
trying to solve div1 D with persistent segment tree
im using two persistent segment trees one to find element before and one to find element after
keep getting MLE no matter what i did
is there a way to do it with one persistent segment tree or am i missing something ?
here's the submission
For Div 1 D problem. Could someone explain me how to determine if some element belongs to all LIS?
you have to count the number of LISes that the element is the head of
and the number of LDSes the element is the head of
and if the number of the LISes in the whole array is the same as multiplying the two calculated values then the element is a part of all LISes
I got that part, but how is the algorithm to count the number of LIS?
i did it using segment tree where for each element the number of ways this element is the head of an LIS is the number of sum of ways each element before it with maximum length LIS
for example : 1 1 3 2 2 4
number of ways: :1 1 2 2 2 6
for 4 we summed ways of 3 and 2 and 2 since 3 and 2 and 2 are the head of length 2 LIS and there are no longer ones
For Div1-B problem, I used binary search to solve the problem but i am getting wrong answer for case 16. i cant figure it out, can anyone help my solution: http://www.codeforces.com/contest/650/submission/16875724
Can anyone explain the approach for Div2 E ?
Didn't get it from the editorial !
How to solve 651A in O(1)?
Can someone give the O(1) solution for Problem A — Joysticks ?
Can someone explain the solution of 651D/650B,
I dont get the tutorial solution... Why do we have to start from the 1st photo only,can't we skip the first photo and then move on the check the other ones, for example in case
5 2 4 13
wwhhw
The answer should be 3 as we can see the pictures 2,3 and 4 ("wwh"),but the algorithm given in the editorial will give answer to be "2", Maybe I dont understand the tutorial,please help,Thanks a lot!
Just realized 650C - Сжатие таблицы was revived in the ACM-ICPC 2017 Regional (Hochiminh City site, Vietnam).
Statement of the problem in the HCMC site
Ah... the nostalgia...
Thanks neko_nyaaaaaaaaaaaaaaaaa for pointing that to me...
Another non-hashing O(nlogn) solution for div1D : My submission
--------------------------------------------------------
The point is to determine whether a element in the initial array must appear in a LIS. My solution is to find the "leftmost" and "rightmost" LIS, and their intersection are the necessary elements which must appear in any LIS.
Definition on the leftmost LIS:
During the process of finding a LIS, for every element E=array[i] we have to find its predecessor P, which is the element before E in a LIS of the subsequence [1...i] containing E as its(refers to the LIS) end.Thus, if we take the leftmost P (which has the smallest index) every time, the final LIS that we get is the "leftmost" LIS.
The rightmost LIS is defined similarly.
Proof on the correctness:
Let's denote the leftmost LIS with L, and the rightmost one with R. Let P be a element in both L and R.
Obviously the index of P in L and that in R are the same. Otherwise there would be a longer increasing subsequence than L or R.
If P's predecessor in L is the same as that in R, it means there can be no other candidates for P.
On the other hand (pred_in_L(P)!=pred_in_R(P)), different predecessors lead to the same P, then it is more inevitable that P is the only candidate!
--------------------------------------------------------
Well, I know this isn't quite a scientific proof, but the solution passed all the tests after all... Waiting for a more rigorous one :)
My solution to C is completely different from the editorial. Its too long to describe too. And it just passed all cases. Here: 92662769