A div2. Required row is row that have only one star inside. Requred column is comumn that also have only one star inside. So, you can iterate over all rows/columns, calculate number of stars inside them and find the answer.
Authors are MikeMirzayanov, Gerald .
B div2. Naive solution O(n3) (where you check all triplets) doesn't fin into time limits.
You can see that for every two points from triplet (for example, for A and C) you can find place of the third point. So you can find number of requred triplets just inerate over all pairs of points and check middle point between points in every pair.
How to fast check position? You can add 1000 for all coordinates (you can see that this operation doesn't change the answer) and mark them in the 2-dimensional boolean array 2001х2001. So you can check every position for point in O(1) time.
Obtained solution works in O(n2).
Authors are MikeMirzayanov, Gerald
A div1. C div2. In this problem some greedy solution expected.
Let fix 2 planets: in planet i we will buy items, in planet j we will sell the ones. Profit of item of type k will be b_jk-a_ik. Every item has size 1, so you should greedy take items in order of decreasing of profits of items while you have place in the hold.
Scheme of full solution: you should iterate over all pairs of planet, for every pair greedy take items and find total profit. At the end you should find maximal total profit over all pairs and output it.
Author is Ripatti
B div1. D div2. You can see that split oparetion is just cyclically shift of string. You can go from any cyclically shift to any other one except the current one.
Let's call some cyclically shift good iff it equal to the final string. All others cyclically shifts we will call bad. You can check all shifts in O(|w|2) time. Let's you have A good shifts and B bad ones.
Let's define dpA[n] as number of ways to get some good shift using n splits and за dpB[n] as number of ways to get some bad shift using n splits.
dpA[0]=1, dpB[0]=0 or dpA[0]=0, dpB[0]=1 according to the first shift is good or not. All other values of dp you can get using following reccurences:
dpA[n] = dpA[n-1] * (A-1) + dpB[n-1] * A
dpB[n] = dpA[n-1] * B + dpB[n-1] * (B-1)
Answer will be dpA[k]. So you have O(|w|2 + k) solution.
Also this problem can be solved in 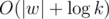 time.
time.
Author is havaliza
C div1. E div2. The second player have easy strategy to hold some chip in position (X, Y) in one of four half-planes — x ≤ X + 2, x ≥ X - 2, y ≤ Y + 2 и y ≥ Y - 2. He can chose one of these half-planes by himself.
So, in case max(|x1 - x2|, |y1 - y2|) > 4 the second player wins — he just holds chips in half-planes that have no common cells.
Cases for max(|x1 - x2|, |y1 - y2|) ≤ 4 expected to solve using some bruteforce. You can see that moving chips in way of distancing from each other is not profitable for the first player. Therefore you can bruteforce the game in square no more than 5 × 5. If your bruteforce so slow and doesn't fit into 2 sec, you can use precalculation. Also you can write some dp using masks.
Also you can check cases max(|x1 - x2|, |y1 - y2|) ≤ 4 by hand. But there you can easy make some mistakes.
Author is Ripatti
D div1. Let's define dp[pre][len] as the minimal prefix of hyperstring that have with prefix of t of length len largest common sequence of length len.
Then you have see reccurences:
dp[pre][len] = min(dp[pre - 1][len], leftmost position of letter s[pre] in t that right than dp[pre - 1][len - 1]).
For finding value of the second part inside min-function of formula above in O(1), you should calculate some additional dp's:
dp1 — for every basic string, positions inside of them and letter you should calculate leftmost position of current letter that right than current position;
dp2 — for every element of array of basic strings (it is hyperstring) and letter you should calculate leftmost basic string that have current letter and this string is rinht than current basic string.
So you have 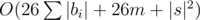 solution.
solution.
Author is havaliza.
E div1. At the first let's try to solve another problem: we have k chosed vertices in the tree and we want to find sum of subtree that "spanned" dy them in time 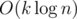 (with any preprocessing time).
(with any preprocessing time).
Let's sort all k vertices in order of dfs traversal — v1, v2, ... , vk. Consider pathes v1-v2, v2-v3, ... , v(k-1)-vk and vk-v1. You can see that they cover only our requred subtree and every edge is covered exactly two times. So you can just find sum of lengths of these pathes (you can do it in required 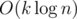 time using LCA algo) and divide obtained value by 2.
time using LCA algo) and divide obtained value by 2.
For solving initial problem you should support set of active vertices in ordered state (for example, you can use std::set) and sum of all pathes between all neighbour vertices. Now you can process insert/remove queries in 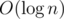 , and recalculate sum of pathes by finding no more than 3 new pathes also in
, and recalculate sum of pathes by finding no more than 3 new pathes also in 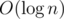 .
.
So you have 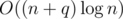 solution.
solution.
Author is Ripatti.











For problem D (div 2) the formula is slightly incorrect. Correction:
Yes, you're right.
Thank you, fixed
In div2 E. Why does the second win when the input is "5 5 1 1 5 4"
Brute force proves it
Did you write the program using brute force and find the regularity before you submit the problem?
Yes I am. But I've got Wrong answer on test 9 and then write brute force.
For div 1 B, I want to know that what are values A and B in the recurrence relations? Also I would like to find some AC submissions to this problem.
For Div1E I have an alternative solution which focuses on binary searching the LCA of a point and a set of points as I didn't noticed that I can double count all necessary path by sorting dfs visiting time.
Code: http://codeforces.com/contest/176/submission/20437271
(Now reviewing the code, the part of getLCA and sparse table is not required for finding LCA between a point and a set of points)
The current length of all necessary path is always updated.
Pre-processing:
dfs for finding the visiting time and ending time of each vertex. O(N)
Pre-calculate the binary exponential distance from each vertex to the 2^N parent. O(NlogN)
The current length of all necessary path is always kept
Keep a segment tree to check if there are any restored village in a sub-tree in O(logN) time, we will need it for the binary searches for the queries.
How to handle queries:
'+': Find two poitns: 1. the LCA of the village being restored with any other already restored villages, 2. the LCA of the new set of points. Update the LCA of all villages if necessary. This can be done in O(logN * logN) time.
'-': Find two points: 1. the LCA of the remaining set, 2. the LCA of the village being destroyed with any other villages that are still available. Update the LCA of all villages if necessary. This can be done in O(logN * logN) time.
Remember to handle cases where the restored villages set size if smaller than 2.
'?': Just return the length value, this can be done in O(1) time.
Total time complexity: O(NlogN + qlogN * logN), which is slightly worse than the intended solution but it still fits in the TL very easily.
O(|w| + logk) solution for 176B - Word Cut (Div 1 B) 96438522