Someday I will arrange C and D correctly :)
Firstly, in case c = 0 we should output YES if a = b else answer is NO.
If b belongs to sequence b = a + k * c where k is non-negative integer.
So answer is YES if (b - a) / c is non-negative integer else answer is NO.
x a y
b m c
z d w
Number in the center may be any from 1 to n because number in the center belongs to all subsquares 2 × 2. So, let's find answer with fixed number in the center and then multiply answer by n.
Let's iterate over all possible x. Sums of each subsquare 2 × 2 are the same so x + b + a + m = y + c + a + m and y = x + b - c.
Similarly, z = x + a - d and w = a + y - d = z + b - c.
This square is legal if 1 ≤ y, z, w ≤ n. We should just check it.
Also we can solve this problem in O(1).
We have array ai and should make all numbers in it be equal to zero with minimal number of operations. Sum of all ai equals to zero.
We can divide array into parts of consecutive elements with zero sum. If part has length l we can use all pairs of neighbours in operations and make all numbers be equal to zero with l - 1 operations.
So, if we sum number of operations in each part we get ans = n - k where k is number of parts. We should maximize k to get the optimal answer.
One of the part consists of some prefix and probably some suffix. Each of other parts is subarray of a.
Let's calculate prefix sums. Each part has zero sum so prefix sums before each part-subarray are the same.
So we can calculate f — number of occurencies of the most frequent number in prefix sums and answer will be equal to n - f.
Bonus: how to hack solutions with overflow?
We have binary search tree (BST) and should insert number in it with good time complexity.
Let we should add number x. Find numbers l < x < r which were added earlier, l is maximal possible, r is minimal possible (all will be similar if only one of this numbers exists). We can find them for example with std::set and upper_bound in C++.
We should keep sorted tree traversal (it's property of BST). So x must be right child of vertex with l or left child of vertex with r.
Let l hasn't right child and r hasn't left child. Hence lowest common ancestor (lca) of l and r doesn't equal to l or r. So lca is between l and r in tree traversal. But it's impossible because l is maximal possible and r is minimal possible. So l has right child or r has left child and we know exactly which of them will be parent of x.
That's all. Time complexity is  .
.
Let the indexation will be from zero. So we should subtract one from all ai. Also let an - 1 = n - 1.
dpi is sum of shortests pathes from i to i + 1... n - 1.
dpn - 1 = 0
dpi = dpm - (ai - m) + n - i - 1 where m belongs to range from i + 1 to ai and am is maximal. We can find m with segment tree or binary indexed tree or sparse table.
Now answer equals to sum of all dpi.










Lightning fast editorial. Respect mate.
And better yet, lightning fast system testing. It's 4:00 JST, and I would've woken up a lot more to see if I passed systests.
Systests are done already?! Blessup
What is the idea for solving B in O(1)?
when comparing x,y,z,w, we can determine which are the smallest and largest, and determine the difference (more important). If the difference is d, than there can be only (n-d) variations for x,y,z,w
Thanks! It turns out I used that exact idea, but I still managed to mess up and had O(N) code as in the following.
n, a, b, c, d = map(int, input().split()) lo = min(a+b, a+c, c+d, b+d) hi = max(a+b, a+c, c+d, b+d) ans = 0 for x in range(1, n+1): ans += max(0, n-hi+lo) #n-(hi-lo) print(ans)facepalm intensifies
I found an interesting solution that scales easily to bigger problems:
Thank you my friends :)
good.I solved the problem like this too.
For problem E, can anyone explain why such dp works? Or how to prove such dp is correct? Sorry for my bad English :)
We want to calculate distance from i to j. If j < a[i] then distance is 1. Otherways, it is optimal to move to cell with maximal a[i] (to maximize our range at next step). That is, distance[i][j] = distance[m][j] + 1, where m is cell with maximal a[i].
Finally understand. Many thanks!
We can simply take minimal dpm+m instead of maximal a[i]. But why it is optimal to move to cell with maximal a[i]?
Choosing the maximal a[i] do not mean we must go to it after this move; it means that there are more positions to choose when we go next (as we can choose any position between i+1 and a[i]). The more choices we have, the better solution we may get.
"The more choices we have, the better solution we may get". Here we are making a greedy move. What is the intution/logic/proof behind it?
That is to say, getting more choices won't make the answer worse. You can choose not to follow this choices, but the answer won't be worse than when we have fewer choices.
Na2a You said that we have to maximize our range at next step, so why isn't it optimal to move to a cell with maximal (a[i] + i) ?
Because range of jump is [i, a[i]] not [i, i + a[i]].
Oh silly question! Thanks!
B: "Let's iterate over all possible x"
How can it be O(1) after this?
He said "Also we can solve this problem in O(1)." So above was O(n) solution, but it could be done for O(1).
Thank you, it's clear now :))
The O(1) solution is mentioned but not actually given. You can use the following formula, n·(max(0, n - max(a + b, a + c, c + d, b + d) + min(a + b, a + c, c + d, b + d))). Proof is left as an exercise to the reader, of course. B-)
can u please elaborate it with example.i am not getting the logic behind it. thanks in advance.
Consider only the four unknown corners of the 3 × 3 box. Note that if any one corner's value is known, the values of the other three corners are fixed. Without worrying about the condition that the 2 × 2 boxes have the same sum, there are n possible sets of values for the four corners (read the previous sentence).
However, say you have n = 5, a = 1, b = 1, c = 2, d = 2. If the bottom-right corner has value 5, the top-left corner must have value 7 for the top-left and bottom-right 2 × 2 boxes to have the same sum. Thus, the number of possible sets of values for the four corners is at most n - greatest_difference_among_{a + b, b + d, c + d, a + c}. This is because these are the fixed values such that if one corner's value is determined, there is only one possibility for the other three corners based on a, b, c and d.
Now consider case n = 1, a = 1, b = 1, c = 2, d = 2. In this case, n < greatest_difference_among_{a + b, b + d, c + d, a + c}. Thus, the difference cannot be compensated for regardless of what four values of n you choose for the four corners. Finally, the total number of sets of values for the corners is max(0, n - greatest_difference_among_{a + b, b + d, c + d, a + c}), or max(0, n - (max(a + b, b + d, c + d, a + c) - min(a + b, b + d, c + d, a + c))) which is the same as my original comment, max(0, n - max(a + b, b + d, c + d, a + c) + min(a + b, b + d, c + d, a + c)).
There is some minimum value for x (let's call it xmin), such that all the remaining variables y, z, w become valid (that is, they are in the range [1..n]).
There is also maximum value xmax that still holds y, z and w in the valid range.
The trick is to understand that for all the values in between xmin and xmax we can always make the triple y, z, w valid.
If xmin = 5 and xmax = 9 then x = 6, x = 7, x = 8 are also valid (we don't need to check them explicitly).
http://codeforces.com/contest/675/submission/17953232
Why codeforces shouldn't know that task D was on HR 23 days ago?
Click
Will be russian version of editorial available?
I think there is a error in the solution to E. m must be chosen from range [i+1,a[i]] not [i+1,n-1]. The code is also given as such
Fixed, thanks
You're correct
For Problem D, my submission 17949387 O(NlogN) got a TLE, while 17954833 passed. Is this because of the test data set, or is the first submission actually slower and if so, why?
The first submission is not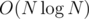 , since it is naive BST and hence might get unbalanced to have O(N) height = O(N2) performance over N insertions.
, since it is naive BST and hence might get unbalanced to have O(N) height = O(N2) performance over N insertions.
My dad, a vietnam veteran, told me that there's one thing that always sticks with kids and adults no matter how old they are.
Napalm.
For problem B, referring to :
"Help Vasya find out the number of distinct squares the satisfy all the conditions above. Note, that this number may be equal to 0, meaning Vasya remembers something wrong.
Two squares are considered to be different, if there exists a cell that contains two different integers in different squares.
Output Print one integer — the number of distinct valid squares."
Is is me who understood that all squares should be distinct (for example the input 1 1 1 1 1 should give 0 because the only answer is a matrix of 1 where the squares are not distinct) or is it the problemset ?
How the solution of C Works? Seriously :O
Example case: 15 0 0 0 -15
The prefix sum: 15 15 15 15 0
As you can see, the answer is 1 since 15 occur 4 times
The repeated prefix sum means there are 4 part which produce zero (in case 15)
Let i is the array position where 0<=i<5
The first part is i=0 and i=4 -> we directly move the money from i = 0 to i = 4 since zero sum is guaranteed.
The second part is i = 1 -> 0 move
The third part is i = 2 -> 0 move
The fourth part is i = 3 -> 0 move
So the answer is 1.
Conclusion number of repeated prefix sum means number of parts if the sum of subarray from 0 to x is the repeated prefix sum.
I've solved E with something like binary-lift. #code
why can this submission accept? http://codeforces.com/contest/675/submission/17948510 who could make a hack data to kill it, help!
Dont understand why we have to choose m such that Am is maximal, it seems like greedy Update: Got it, larger am will always cover other choices
can someone explain the o(1) solution for problem B? i did it in o(n);
You have 3 different explanations from above :) Ask clarifying questions to one of those comments.
Problem D is almost same with this problem: https://www.hackerrank.com/contests/womens-codesprint/challenges/mars-and-the-binary-search-tree
How to hack this O(N^2) solution?? http://codeforces.com/contest/675/submission/17956511
Can anyone explain the solution of problem C ?
Suppose that the money is as follows ----> -1 2 -3 5 3 -6
Then the prefix sums will be -----> -1 1 -2 3 6 0
Since the highest frequency is 1 so our k=1 and answer = N-1
Another Example be ------> 15 -5 5 -15
Prefix Sums ---> 15 10 15 0
15 is repeated twice so answer = 4-2 = 2 transfers one from 15 to -15 and 5 to -5
A segment of x bank accounts which sums to zero needs x-1 money transfers to make all bank account money =0 .
For eg:- 5 0 -5
i) First we transfer 5 from first bank account to second bank account. Now accounts look like this 0 5 -5 ii) Then we transfer -5 from second bank account to third bank account. Now accounts look like this :- 0 0 0 Thus is 2 ( 3-1 ) transfers I made all account's money to zero.Now suppose there are k segments in given array whose sum is equal to zero. Let length of segments be x1,x2,....,xk .
Now for first segment we take x1-1 transfers , for second x2-1 .... and for kth xk-1 transfers.
Total number of transfers = x1-1+...... xk-1 = (x1+x2+x3+....xk)- (1+1+...ktimes) = n — k
If we want to minimize total number of transfers we have to maximize value of k( Remember we assumed number of segments to be k )
So what can we do to maximize value of k ?
Let f[1],f[2],f[3],....f[n] denote cumulative sums of given array.
f[i] = a[1] + a[2] +.... a[i]
f[j] = a[1] + a[2] + ..... a[j]
Suppose f[i]=f[j] then
a[1] + a[2] +.... a[i] = a[1] + a[2] +.... a[i] + a[i+1] + .... a[j] Therefore , a[i+1] + a[i+2] +..... a[j] =0 Also since the sum of array as a whole is given to be zero . Remaining array sum is also zero. a[j+1] + a[j+2] .... a[1] + a[2] + .... a[i] =0Therefore we got 2 segments with sum =0 when we had two cumulative sums same.
Now suppose f[i] = f[j] = f[k] for some 1<=i,j,k <=n , i<j<k
Therefore a[i+1]+....a[j]=0 a[j+1]+....a[k]=0 a[k+1]+....a[1]+...a[i]=0
Therefore try to find the frequency of most frequent cumulative sum and reduce it from n to get answer.
Hope it helps.
Great Explanation Mayank Pratap. Codeforces should hire you to write editorials.Then it will a lot easier.
Godspeed Bro.
Best explanation on C I've read. Thank you.
At last understand it..simply awesome.
but how to handle the case when the segment is a prefix and a suffix ?
Thanks for nice explanation. I thought the solution over 2 hours. Finally, I could understand this problem after reading your explanation.
thx :)
Can anyone explain how problem C solution hit your mind. I mean to say how to have a good proof for that.
hope my explaination helps.. ;)
Thank you ! But i already solved that one :)
Can someone provide a more detailed explanation for problem C ?
Can somebody explain why Solution C "prefix sums" is correct answer? thanks.
See this
Obviously the answer is less than the number of banks, which shows that when you put all these banks on a ring and use some roads to connect these banks, there are at least one road where no money goes through in the optimal way.
Let's cut one road, break the ring into a list and iterate all the banks. It is easy to see that whenever the prefix sum becomes zero, we can find a way to transfer money in the banks we have iterated so we can cut the next road.
Now we just need to iterate the road we cut at first and maintain all prefix sums. Every time we fix the current road and cut the next road, all prefix sums would simultaneously increase or decrease by a number, which depends on the order you iterate, so we just need to maintain the offset.
Can anybody provide a more detailed explanation for DIV2 E?
In Problem B, why are we multiplying the answer by n?
note that center '?' can be in range 1~n, whatever other '?' is.
Actually I don't know what is happening but when I run my c++ program on my laptop for Codeforces Round 353 Problem D, it gives correct result, but when I run it on codeforces, it gives different result. It is not that it has happened to me first time. So I would request you to please have a look at this so that I do not face this problem in future.
Code link: http://codeforces.com/contest/675/submission/17955668
I don't know how this works in your computer but one of the problems is here :
when it==my.end() , then it isn't element, so haven't .first ! if you used -- for going back before using it, you must write it like this --it.
also notice that in every place you used it--, it's value is really changed and isn't temporary.
I have changed from it-- to --it. It has passed the first test case but the problem is still there as it failed the 2nd test. You said that "also notice that in every place you used it--, it's value is really changed and isn't temporary.", but I am overwriting its value in each iteration.
New code submitted: http://codeforces.com/contest/675/submission/17962900
I didn't say that you must change all
it--to--it. I just want to note their difference for you .and for 2nd test check these part of your code :
Hello. How to use spoilers ?
Choose last drop down in writing window, then click on spoiler. Add your text between > and <
Some comments:
In problem C, As mentioned in the tutorial, a segment of x bank accounts which sums to be 0 needs x - 1 transfers to make all bank accounts to be 0. So the basic idea is to break the whole circle into as many such segments as possible. Suppose the prefix sum are f[1], f[2], ..., f[n]. For any i and j, if we have f[i] = f[j], then a[i+1] + a[i+2] + ... + a[j] = 0 and a[j+1] + a[j+2] + ... + a[n] + a[1] + a[2] + .. + a[i] = 0. So, the problem can be transferred into a problem of finding the mode of the prefix sum list.
In problem E, Since we have dpi = dpm - (ai - m) + n - i - 1, i + 1 ≤ m ≤ ai, we can also find maximal dp[m] + m rather than maximal a[m]. The idea of finding maximal a[m] comes from the intuition that we can reduce the answer if we go to a city which can go to as many cities as possible. The idea of finding maximal dp[m] + m comes from the formula itself. So I think finding maximal dp[m] + m will be more rational.
Problem B: How to be sure that 64-bit integer will be enough for total valid combinations count, and there is no need to use
BigInteger? It's seems that total valid and invalid combinations count is10^5*10^5*10^5*10^5*10^5 = 10^25which obviously can't be represented by 64-bit integer.There is only 10^5 * 10^5 different correct positions, because every position can be set by two numbers
Hi, For problem D, I have the following submission http://codeforces.com/contest/675/submission/17953025
It uses a balanced binary search over the possible intervals so it's clearly O(n*log(n)). Yet, it timesout on test case 7. Solution is similar to the proposed one, so I guess the only thing that slows it down to get a timeout is the fact that C# is slower than C++, which might not be fair taking into account that it shouldn't be about what language you use.
I might be wrong and not realise the test-case where it's not O(n*log(n)), but I really can't see how.
Your algorithm has problems when the input is a decreasing array. It has nothing to do with the speed difference between C# and C++.
Can you give more details or a test-case I can try? Tried 3 / 3 2 1 and it seems to work fine.
The problem is that its time complexity is O(n^2) for decreasing arrays. You have the test case. Just try appropriate size, like 10^5.
That's not true. Binary search over an inverse-sorted array is still O(log n). I have just tried it and for 100k descending value elements it makes 1468961 comparisons inside the binary search. Less than n*log2(n)
Found the problem. It seems that C# Insert and Remove are O(n) operations.
Hello guys, Can someone tell me why is my solution for D receiving TLE ? I am pretty sure i am adding elements here in log N p.e and printing out solution per node in log n... Submisson: http://codeforces.com/contest/675/submission/17963314
Cheers!
You code a solution that's O(n) for every insertion. Test it locally with:
The tree generated with this has a form like a list: 1 -> 2 -> 3 -> ...
So, for every insertion you transverse all the tree, since, O(n)
I solved problem D using segment tree RMQ but I didn't have the time to code it during the contests .
submission : 17964060
nice one.... I like the approach
There is simpler solution of problem D: 17964559 Idea is: for each "child place" (i.e. place where new node can be added) we keep minimal number which will be placed there.
Can someone explain what is wrong with my solution of problem D ? My code link
Hey, I am still not able to understand the solution for problem C. :/ If someone could help me see the solution in a simpler way ? i went through the comments where this comment was suggested. I still couldnt figure it out. From the editorial i have understood the part till dividing it into parts and if length l the l-1 operations so if k parts ans = n-k. After this i cant understand. Any help please ?
could somebody plz explain D in a bit more detail!!
Sorry if my explanation is tedious.
Let's consider the second example: 4 2 3 1 6
At first, our BST is empty, so the root value will be 4. That means that all values that lie in the interval [1, 3] will go to the root's left, and all values that lie in the interval [4, 10^9] will go to its right.
So, at the moment we have two candidate places to put our next number: [1, 3] (value=4) and [5, 10^9]{value=4}.
If we insert the next value we find that it should to go the root's left because 2 is in [1,3]. Since we have filled the root's left children, we must remove the interval [1, 3]{value=4} and add two new ones: [1, 1]{value=2} and [3,4]{value=2}. So now we have the following candidates: [1, 1]{value=2}, [3,4]{value=2} and [5, 10^9]{value=4}.
If we do the same thing with all sequence values we will know all parent values and we will keep an updated information about where new values should go. It is not necessary to keep the empty intervals (i.e: those that its right value is smaller than its left), since that means that no value can be a child of that node.
In order to know quickly on what interval a new value should go you can keep them sorted by its right values, then for a number x find the first interval right that it is greater or equal than x. You can do this because you know the interval is unique (as the BST paths are).
You can check my solution for more clarification: http://codeforces.com/contest/675/submission/18001556
You solution seems buggy to me. Could you please explain how does set::upper_bound() select the proper interval from the set. Shouldn't it be set::lower_bound() instead?
As per my understanding, if the set contains three interval,
i.e. [1,1]{2}, [3,3]{2} and [5,1000000000]{4}
and now I insert the element 3, upper_bound({3, 3, 3}) should select the interval [5,1000000000]{4} (see the definition here). Clearly, this messes up the solution.
Let me know, if I am wrong here
.
lower_bound is first ">=", upper_bound is first ">". Yes, names are very confusing.
Can somebody explain why in problem E we should change the indexing to 0-based?
Using the reasoning described in the editorial the dp formula I find is:
dp[i] = dp[m]+(m+n)-(a[i]+i),
which works just fine.
I don't see however why the indexing should affect our formula and why it comes out different.
It was just more comfortable for me to use 0-based indexing. You can use 1-based indexing if you want.
Can someone please explain how is the recurrence dpi = dpm - (ai - m) + n - i - 1 actually derived. I understand that for any pair i,j dp[i][j] = 1 + dp[m][j] where m is the index which has the greatest value of ai. Yet, I fail to understand how is the recurrence derived from it ?
thanks, in advance!
Yes, I know that editorial for E is too short, sorry about that.
ρi, j = 1 for j = i + 1... m
ρi, j = ρm, j = 1 for j = m + 1... ai
ρi, j = 1 + ρm, j for j = ai + 1... n - 1
Sum of ρi, j for j = m + 1... n - 1 equals to dpm + n - 1 - ai
Sum of ρi, j for j = i + 1... m equals to m - i
So, sum of ρi, j for j = i + 1... n - 1 equals to dpi = (dpm + n - 1 - ai) + (m - i) = dpm - (ai - m) + n - 1 - i
ρi, j = ρm, j = 1 for j = m + 1... ai
This is only possible when a_m >= a_i, which may not be necessary. Am I going wrong somewhere?
We must choose maximal possible am because we want to maximize range on the next step.
aj ≥ j + 1 for each j by the statement.
am ≥ ai + 1 if we choose m = ai. So, maximal possible am ≥ ai + 1.
Ahh, it suddenly struck me. Thanks for the beautiful problem. I can sit whole day long just admiring the problem.
For problem E, where did (a_i — m) come from? Doesn't that assume that a_m >= a_i?
In problem D, st.upper_bound(a); gives AC http://codeforces.com/contest/675/submission/18177277 whereas upper_bound(st.begin(),st.end(),a); gives TLE. http://codeforces.com/contest/675/submission/18177176. What could be the reason...?
Can somebody explain me how this greedy approach works in Div 2 E.(ie) choosing the m from the maximal a[i].Can you give me a more formal logic or proof for it? According to me it should be dp[i]=max(dp[m]+m-i) where m belongs to [i+1,a[i]] which makes it a n*n*log(n) approach instead of n*log(n)
Hope, those comments will be useful for you: first, second
Your formula is a bit wrong. But even if it was right I don't understand why it's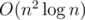 . If we calculate dp naively we get O(n2) solution. Also we can keep dpm + m in segment tree and find maximum in
. If we calculate dp naively we get O(n2) solution. Also we can keep dpm + m in segment tree and find maximum in  what leads to
what leads to  solution.
solution.
In DIV-2C — "So, if we sum number of operations in each part we get ans = n - k where k is number of parts." Can anybody provide me a prove of this statement? How to verify its correctness?
komendart Please Explain the dp transition and describe why does it work. I can not understand this transition of dp calculation.
Wow I use DFS which turns out to be such an overkill for problem C: hahaha