Remember to register.
--- EDIT, the contest is over ---
BearBall, 250 points
There is a special case when all points are in one line. Otherwise, for any pair of bears the number of throws is 1 or 2.
So, for each points you should count how many points are directly reachable from this one. You achieve it by sorting other points. The complexity should be 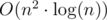 .
.
BearGridRect, 600 points
Hint: use flows, maybe mincost.
BearCircleGame, 800 points
Dynamic programming. Iterate over the number of remaining players, from n to 1. In each moment, you need an array of size with probabilities — for each number of bears what is the probability that Limak is this far from the starting bear. Then, for each bear we need probability that he loses and thus we will know the next array (for remaining - 1 remaining bears).
a loses with probability  .
.
Try to first write O(n3) approach — find cycle in a sequence of indices a + 1 - k, a + 1 - 2k, a + 1 - 3k... and then over indices in the cycle sum up 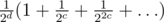 where c is the size of cycle and d says which place this index has in the cycle.
where c is the size of cycle and d says which place this index has in the cycle.
To make it faster, notice that the answer for a and for a + k will be similar. It's enough to multiply (or divide, whatever) by the sum by two, and then add one value.
WINNERS
And congratulations to Petr for solving all problems and thus winning the parallel round.











That was a bit of spoiler.
Btw, problem 600 can be solved without using mincost-flow, but using an LR-max-flow algorithm (for finding maximum flow when there are lower bounds of flows for each edge).
Problem 600 can be solved with maximum matching (with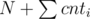 vertices on each side).
vertices on each side).
Nice, I didn't expect that. How to do it with matching?
As I see, the first part contains N rows and cnt[i] vertices for each rectangle -- placeholders for columns that are supposed to cover by marked cells in rectangle.
The same holds for the second part, but for columns and rows' placeholders.
Btw, thanks for such interesting problems!!!
What's wrong with the solution using bfs for the 250 pointer ?
There could be O(N2) edges, so the complexity could be O(N3) right?
This can be overcome by breaking out of the BFS as soon as all vertices are visited.
Did that in last minute but failed systest because of integer overflow -_-
Small clarification, this would only speed up BFS in practice right?
I mean, consider some graph with N / 2 nodes with all pairs of edges connected. the rest N / 2 nodes connected as a chain with this main component. Here BFS from any of those nodes in main component will be still O(N2) right?
Yeah, it does not help the asymptotic behavior in the general case. But in this problem, BFS becomes O(N) instead of O(N2), for the same reason the more clever solution works.
Lol there's nothing wrong when you do a bit of optimization such as returning when all of the vertices are in the queue = ))
Why did you set the time limit for the 800-pointer two times the usual 2s?
I tried to write my Java solution to be as slow as reasonably possible. It requires ~2s for the current constraints so I chose 4s to be TL.
But you may ask why I chose high constraints. Well, to not be afraid about O(n3) approach. In hard problems it's a disaster when people get worse complexity accepted so it's very convenient for me to set high constraints. I think that everything would be fine today with lower constraint for n but I also don't see important pros.
My screencast
Slightly unrelated, but what tool are you using for opening problem statement in browser and coding in Dev C++ instead of the arena?
It is really tough to use the arena(UX wise)
Actually, I just started to use Greed and I like it. Previously I used KawigiEdit. There are some nice posts about Greed on Vexorian's blog. For what it's worth, my config is the following:
(replace DOLLAR with dollar signs).
In your code for BearCircleGame, I believe that is a geometric series not an arithmetic series. Please correct me if I'm wrong.
Thanks, corrected now.