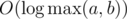Блог пользователя skpro19

Help needed in a number theory problem
Автор skpro19, история, 8 лет назад, По-английски

The problem is this.

The tutorial says this:

"If a fraction can be obtained with k resistors, then it is simple to calculate that we can obtain fractions and with k + 1 resistors. So adding one resistor means performing one operation backwards in Euclidean algorithm. That means that the answer is equal to the number of steps in standard Euclidean algorithm.

At first we thought about the major problem (any two elements can be joined), but had a moment of eureka and got that the given problem unexpectedly naturally can be reduced to GCD. "

I do not understand the tutorial. A little help will be really appreciated.

Thanks!

  • Проголосовать: нравится
  • +1
  • Проголосовать: не нравится

»
8 лет назад, # |
← Rev. 2   Проголосовать: нравится +2 Проголосовать: не нравится

Resistances of all possible elements are:

  1. one resistor — 1
  2. an element and one resistor plugged in sequence — greater than 1
  3. an element and one resistor plugged in parallel — less than 1.

So if you are given a target resistance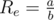 , there is only one possible way to construct it:

  1. If Re = 1 (a = b), use one resistor
  2. If Re > 1 (a > b), use an element e' and one resistor in sequence so that Re = Re' + 1. Or, equivalently, .
  3. If Re < 1 (a < b), use an element e' and one resistor in parallel so that . Or, equivalently, .

In the second and the third cases you now need to build an element e', and it can again be done in only one possible way (depending on whether Re' is greater than, less than or equal to 1). By continuing these steps we get a sequence of resistances , such that the next pair (a, b) is obtained by the previous by subtracting the smaller element of the pair from the larger one. We can now build this sequence naively, but it will take too much time in case, for example, a = 1018, b = 1.

We can make a shortcut by subtracting the smaller value multiple times at once. Say, a > b, then a = kb + r, where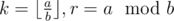 . So if we subtract b from a k times, we obtain the pair (r, b). This is essentially the GCD algorithm (except we calculate the sum of all values k in addition to 'normal' calculations), so it works in

→ Ответить