710A - King Moves
Easy to see that there are only three cases in this problem. If the king is in the corner of the board the answer is 3. If the king is on the border of the board but not in a corner then the answer is 5. Otherwise the answer is 8.
Complexity: O(1).
710B - Optimal Point on a Line
The function of the total distance is monotonic between any pair of adjacent points from the input, so the answer is always in some of the given points. We can use that observation to solve the problem by calculating the total distance for each point from the input and finding the optimal point.
The other solution uses the observation that the answer is always is the middle point (by index) in the sorted list of the given points. The last fact is also can be easily proven.
Complexity: O(nlogn).
710C - Magic Odd Square
The problem was suggested by Resul Hangeldiyev Resul.
The solution can be got from the second sample testcase. Easy to see that if we place all odd numbers in the center in form of rhombus we will get a magic square.
Complexity: O(n2).
710D - Two Arithmetic Progressions
I wanted to give this problem a lot of time ago. I thought it is very standard problem, but I underestimated its difficulty.
Let's write down the equation describing the problem: a1k + b1 = a2l + b2 → a1k - a2l = b2 - b1. So we have linear Diofant equation with two variables: Ax + By = C, A = a1, B = - a2, C = b2 - b1. The solution has the form: 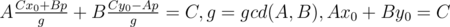 , where the last equation can be solved by extended Euclid algorithm and p is any integral number. The variable p should satisfy two conditions:
, where the last equation can be solved by extended Euclid algorithm and p is any integral number. The variable p should satisfy two conditions: 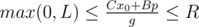 and
and 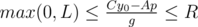 . The values A and B are fixed, so we can get the segment of possible values for the values p. The length of the segment is the answer for the problem.
. The values A and B are fixed, so we can get the segment of possible values for the values p. The length of the segment is the answer for the problem.
Complexity: O(log(max(a1, a2))).
710E - Generate a String
The problem was suggested by Zi Song Yeoh zscoder.
This problem has a simple solution described by participants in the comments.
My solution is a little harder. Let's solve it using dynamic programming. Let zn be the smallest amount of time needed to get n letters 'a'. Let's consider transitions: the transition for adding one letter 'a' can be simply done. Let's process transitions for multiplying by two and subtraction by one simultaneously: let's decrease the number 2·i i times by one right after getting it. Easy to see that such updates never include each other, so we can store them in queue by adding the new update at the tail of the queue and taking the best update from the head.
The solution is hard to describe, but it is very simple in the code, so please check it to understand the idea :-)
Complexity: O(n).
710F - String Set Queries
The problem was suggested by Alexandr Kulkov adamant.
Let's get rid of the queries for deleting a string. There are no strings that will be added two times, so we can calculate the answer for the added (but not deleted strings) and for the deleted separately and subtract the second from the first to get the answer. So we can consider that there are no queries of deletion.
Now let's use Aho-Corasik algorithm. The only difficulty is that the strings are adding in online mode, but Aho-Corasik algorithm works only after adding all the strings. Note that the answer for the given set of strings equal to the answer for any part of the set plus the answer for the remaining part. Let's use the trick with converting the static data structure (Aho-Corasik in this case) to the dynamic one.
For the set of n strings let's maintain a set of no more than logn sets of the strings with sizes of different powers of two. After adding new string we should move the sets from the lowest powers of two to the largest until we got an invariant set of sets.
Easy to see that each string will be moved no more than logm times, so we can process each query in O(logn) time.
Complexity: O((slen + m)logm), where slen is the total length of the string from the input.











In problem B , How do we prove that "the answer is always in one of the given points" .
Sort the array, and just find the median.
Why we can forget about them ?
Because, they're part in the answer is length of the interval, and we can just add this interval in final sum, and then forget
I just want to detail TaTaPiH's answer a bit more, but he has 100% of the credits (thanks btw).
Let the two points be x1 and x2. If you take a point y between x1 and x2 (x1 <= y <= x2) the sum of distances to get to y is (y — x1) + (x2 — y) = x2 — x1, which means that independent of the point y you take, the total distance will be the same (the length of the segment).
Let's sort array x which has the n points, 1-indexed. For example, suppose n = 5. We want to minimize the total sum of distance to some selected point y.
Consider points x[1] and x[5]. These 2 points alone will always sum (x[5] — x[1]) to the final sum of distances if you choose some (any) point y between them. (See case n = 2 for explanations). So let's sum that to the final sum and move on.
Now we're left with points x[2], x[3], x[4]. For points x[2] and x[4] you should also take a point y between them, because otherwise a point y outside points x[2] and x[4] would sum something greater then the length of that interval to the final answer. Note that a point between x[2] and x[4] is a point between x[1] and x[5] so you can continue this logic without changing the answer for the previous points. Now only one point (x[3]) is left, see case n = 1.
So the pattern is: you fix 2 extremes points (one to the left and one to the right), now you'll now that an optimal answer must choose a y between them, and move on to the next points, until you're left with 1 or no points.
Assume that we are moving a point from left to right to get the optimal answer, consider the following scenario. (X denotes a point, # denotes the current chosen point)
(XXX m points XXX) # (XXX n points XXX)
Whenever you move to the right, the resulted total distance changes by n-m since you are moving closer to n points and moving away from m points. At one point, when n becomes smaller equal than m, you need not to continue go right for the answer since we only need the leftmost point as the answer. Hence, the answer is always one of the given points.
Where is english version?!
Google translate
Does'nt seem to be working well
English version please? :(
This round is important and must have an English Editorial.
Codeforces is a good international site.
Please don't limit us by only releasing in Russian. I kindly request you to release an English version.
A lot of people are making a great effort to learn english to understand and take place in the community. Are U serious with this EDITORIAL in russian? I hope an english version release of this editorial.
In particular I am very interested in the solution for problem F.
Sorry for the delay with English editorial. I'll write it as soon as I can.
TNX ;))
Now,Thanks!
Longing For Solution in English...
Can someone please explain to me the logic behind problem E. I have used a 1-D array to store the least time to generate i no. of a's.
Let dp[i] be the optimal cost to produce string of length i. We have two cases:
If i is even, then the optimal cost for dp[i] is the minimum of dp[i-1] + x (add new char) or dp[i/2] + y (copy from half the length)
If i is odd, then the optimal cost for dp[i] is the minimum of dp[i-1] + x (add new char) or dp[(i+1)/2] + x + y (copy then remove). For example, you can get string of length 15 either by adding from length 14, or copy from length 8 then removing 1 character
(Note: I don't know if this is the logic used in the editorial code)
I have previously implemented the same.But it is showing incorrect. This approach fails in the following case.
Suppose we want to produce the string of length 30 then according to above approach dp[15]=min(dp[8]+x+y,dp[14]+x)
dp[30]=min(dp[15]+y,dp[29]+x)
you can see that we are having an extra x seconds(which is the same time spent in removing an extra 'a' generated from doubling 8 a's) while calculating dp[30]. Now if we want to produce a string of higher length then there would be more and more extra x seconds while calculating the cost.Hence this approach won't work.
First of all, how do you know that dp[15] must be dp[8] + x + y? It could also be dp[14] + x, depending on the x y values.
Secondly, I don't quite get what you mean by "more and more extra x seconds", but looking at your submissions, I guess your mistake is implementing the dp when i is odd as min(x + v[i/2] + y, v[i-1] + x). It should be v[(i+1)/2]
I don't get something
Lets say i is even, then you that dp[i] is the minimum of dp[i-1] + x or dp[i/2] + y, but why can't it be dp[i+1]+x, like if we can get to 31 faster then to 29, and we need to get to 30. Same question if i is odd.
EDIT: Nvm figured it out
Can you please explain why we aren't considering dp[i+1]+x, I am having the same doubt?
for those still having this doubt..
consider the case when i is even say 30..then one possible choice for making 30 is cost(30)=cost(15)+y which is considered in the above recursion...but another possible choice can be cost(30)=cost(16)+2*x+y when cost(16) is lesser than cost(15)..in this case cost(15) maximum value can be cost(16)+x..so replacing the maximum value of cost(15) in the equation cost(30)=cost(15)+y it becomes->cost(30)=cost(16)+x+y which is still lesser than cost(16)+2*x+y...so when i is even we can say that its optimal answer will be among cost(i-1)+x and cost(i/2)+y only..
we can similarly prove it for the odd case..
can u please explain dp recurrence a little?
I solved problem 710E - Generate a String using Dijkstra, but it got AC with 1918ms :D almost TLE
could anyone explain the other solution using Dynamic programming?! i did not understand what is written in the editorials!!!
Hi, my interpretation of the solution was that instead of using Dijkstra, they managed to use a slightly-different graph that was a DAG, so finding shortest paths is O(N).
You can note that between doubling operations (after the first one, of course), there is at most one + or — operation, because otherwise you could be more efficient by moving them before the previous doubling operation. (for example, the sequence +*++ -> 4 could be done as ++*). If you take a graph with only these edges, it becomes a DAG, and dijkstra is not necessary.
EDIT: Here is incredibly simple solution with this idea http://codeforces.com/contest/710/submission/20469970
Amazing idea!!
Incredible!!
But it seems more acurate to say there is at most one
+or-after*, because*++can be replaced with+*and*--can be replaced with-*. With this statement we know if there exists*in the path, the end of the path is one of*+,*-and*.If you say "there is at most one
+or-between two*, there can be more than one+or-after the last*", it contradicts the above statement.Can I see your code please? my code works with Dijkstra but I got TLE I wanna see if I can do any thing about it!
Did anyone solve problem D?
I know how to derive x0, y0, where Ax0 + By0 = C by using Extended Euclidean Algorithm, but I don't know proceed from here to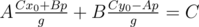 . Also, it seems to me that
. Also, it seems to me that 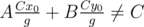 . Am I misunderstanding something? If not, can somebody perhaps elaborate more on this step? Thank you!
. Am I misunderstanding something? If not, can somebody perhaps elaborate more on this step? Thank you!
Also obviously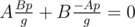 , so the first equation is also true.
, so the first equation is also true.
The only difficulty thing is to prove that all solutions can be described in the given form. It is a standard fact and I think you can easily find the prove in the internet.
I found that no one can solve Problem F by Java 8 because of TLE in test case #19 (demands flush*300000) though problem statement refers to Java's flush.
Did writers&testers check whether it can be solved by Java 8?
What is the "floor (y0*C, A)" in the end of problem D's code for? Why is it here ? How did we get to "y0*C/A" ?
Proof of Problem E , DP — Solution
Hello can someone explain why I got a TLE on test B?
Here is the code: https://codeforces.com/contest/710/submission/91295249.
I believe it is because I use Java but I am not sure. Is that correct?
In ques D, I first calculated solution of x0,y0 using extended Euclid algo, and then i found the value of x=a1*x0+b1, and from their i found the req. resutlt as possible solutions will lie at a jump of lcm(a1,b1) from x. BUT, while calculating x, x is getting overflow because of large value of x0 and a1, in test case 78, can anyone tell me how to solve it. Thanks
I have a (logn)^2 approach to solve problem, could be reduced to O(logn) if map is not used.
I have a assertion that,
let j=log2(i); the best way to reach i is,
1). either reach j and then use operation 1 (x) to reach i.
2). either reach j+1 and then use operation 1 (x) to reach i.
3). if i is even then reach (i/2) and use operation 2 (y) to reach i and if i is odd then reach (i/2 and do operation 1 and operation 2 to reach i) or reach (i/2+1 and do operation 1 and operation 2 to reach i ).
These are the possible best transitions, and we easily calculate best way to reach i if i is power of 2.
My submission:- https://codeforces.com/contest/710/submission/93869685
Problem F — String Set Queries can be solved using hashing. It seems easier to me than Aho-Corasik solution.
Wow, I actually managed to solve a 2400 problem without looking at the solution! >.<
I have a different solution than the editorial. There's no need for Aho Corasick, finite-state machines, tries, or anything like that. It's just suffix array and hashing.
So once we construct our suffix array, we can effectively partition things into "blocks". So like say we have the string "caccc"; then the suffix array will correspond to:
accc
caccc
c
cc
cc
At the first iteration, we have several "chunks" of blocks which are the same
accc
caccc
c
cc
cc
At the second iteration, once we look at prefixes of suffixes of length two, we have some more chunks:
accc
caccc
c
cc
cc
And so forth. Effectively, at the $$$i$$$th iteration, all chunks correspond to suffixes whose prefixes of length $$$i$$$ are the same. It's easy to update these chunks: offline, check the least common prefix between pairs of consecutive entries in our suffix array and make a new chunk divider at that point. If we use some dynamic data structure, like a set, to keep track of chunks, the complexity of this chunk-finding is $$$O(|S| \log (|S|)$$$.
For each chunk, we want to know if it's corresponding prefix of length $$$i$$$ is in the array. That will be $$$O(|S| \log (|S| \cdot \sum {\text{# of chunks at ith iteration}})$$$. That's pretty bad because we could have a lot of chunks.
But actually, a lot of chunks are useless. If a chunk does not correspond to a prefix of anything in $$$D$$$, we can ignore it.
But how do we know if a chunk corresponds to a prefix in $$$D$$$? I used hashing. So I hashed all the prefixes of elements in $$$D$$$ using a rolling hash. Then I put all those hashes into a map. Then, I rolling hash the corresponding prefix-suffix chunk thing in $$$S$$$. And check if it's in the map.
To find the answer, at each iteration, check if a chunk corresponds to something in $$$D$$$ (again can be done using hashing).
Code is kind of long (265 lines long). Most of the code comes from generating the suffix array and hashing (I used 3 hashing moduli to ensure no collisions). So it's actually not as long as it seems.
The end.