In the very beginning of this post I would like to thank everyone who contributed to make this contest happen — both onsite and online versions. Thanks a lot to GlebsHP for helping to organize mirror on Codeforces.
Last year there were 4 teams that solved all the problems before contest ended so we tried to make this year's problems a bit harder. I would also like to mention that 2042 teams registered to this contest,676 managed to solve at least one problem and there is 1 teams that solved all the problems before contest ended. Congratulations to everybody!
Congratulations to tourist and VArtem for winning this competition!
Ok, so here is top 10 of Codeforces version of Bubble cup:
| 1 | 1322: tourist, VArtem |
| 2 | Um_nik |
| 3 | anta |
| 4 | m3m3t3m3: JoeyWheeler, gongy, rnsiehemt |
| 5 | NanA: jiaqiyang, ExfJoe, AcrossTheSky |
| 6 | Moscow IPT Jinotega: Arterm, ifsmirnov, zemen |
| 7 | HellKitsune |
| 8 | MLW: sokian, Merkurev |
| 9 | uwigmanuke: uwi, snuke, sigma425 |
| 10 | BSUIR POWER: andrew.volchek, netman, teleport |
All of them will get T-shirst. But apart from them, as we promised, there will be 10 T-shirts more sent to randomly chosen teams, here they are:
- 95 Singapore zhsh
- 26 Japan natsugiri
- 19 Russia Cryptozool0.6y: Golovanov399, Kostroma
- 12 Rekine: kpw29, Reyna
- 65 China Will not Easily Go Die: wyxoi, Arturia, FHW_SO_WALL
- 82 AkaneSasu
Editorial will be added in a few hours
I am sorry for it taking so long time: problems' authors live all over the world and it took several days rather than hours to assemble it. Editorial for geometry problem will be added as soon as I get it from the author, all others are here











You said there will be 10 T-shirts for random competitors, not teams!
I also said that whole teams will be getting T-shirts. It would be strange if in a team one gets T-shirt and others dont
I agree, but choosing the teams in this way is not fair, as the probability of getting a t-shirt when you're in a team of 1 is different than if you're in a team of 2 or 3.
Can you please share standings of the onsite contest?
That is all I have now
Editorials ?
In "few hours".
there should be some range of "few hours".
In "few years".
in few decades
in few centuries.
in few Millennium.
maybe infinite
i just came here looking for tutorials
Who's from 2022 looking for tutorials?
well google it u will find a doc having solutions
can you tell where did you find the doc of solutions
editorial is loading...loading...loading
Editorials ?
we will upload that in "few centuries"
few "forevers"*
How to solve B ?
Deleted
Looks like on test time and O(n) memory.
time and O(n) memory.
100000000 1 100000000
solution for problem B from editorial will work in
Can you please explain your solution of square root complexity?
The main idea is the same as in editorial. How many vertices with cost x·c0 + y·c1 (I mean vertices with x zeroes and y ones)? It is Cxx + y. Now I want to find the (n - 1)-th vertex in non-decreasing order of cost. I will binary search that cost and check if there is enough vertices with this cost or smaller. Now I want to calculate the number of vertices with cost no more than W. For fixed y: x have to be smaller or equal to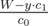 . If y = 0 than all the Cxx + y = 1 and we can calculate its sum in O(1). For all other y we will try all the x and maintain Cxx + y.
. If y = 0 than all the Cxx + y = 1 and we can calculate its sum in O(1). For all other y we will try all the x and maintain Cxx + y. time? Because for fixed y we will try no more than
time? Because for fixed y we will try no more than 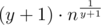 variants of x or the sum will become greater than n.
variants of x or the sum will become greater than n.
Why will it work in
After finding maximal cost I have to calculate the answer. It can be done in a similar way, please refer to my code.
You are right.
We apologize for this. Indeed our solution works in O(NlogN) time and O(N) memory at your test. None of us notices that, we are sorry. Edge test cases contained tests like 10^8 0 10^8, but did not have tests 10^8 1 10^8, our solution works well on tests when 100 <= cost <= 10^8 (and only this kind tests we had). I guess complexity is something like O((maxCost/minCost + logN)*logN), though can't be sure anymore.
If you don't mind I will mark our solution as wrong in editorial and add your square root complexity. Again we are sorry.
Actually there was an idea for a different solution, one with complexity O(log^2(n) log(n c0) ).
Let's assume that c0<=c1. The tree construction from editorial can be viewed in a different way: We have an infinite binary tree with some cost assigned to the nodes. We assign c0+c1 to the root. The cost for the left child is cost of parent + c0 and cost for the right child is cost of parent + c1. We want to select the subset with minimum total cost, since total cost equals to the problem's answer. For the sake of simplicity, before we proceed let's add (c0+c1)*(n-1) to the answer and subtract c0+c1 from every cost.
Let's do binary search on the biggest cost, that we are going to use. To do so, we will need to be able to count the number of nodes with cost, less or equal to C. To count them we use the fact, that it is never necessary to used more than log2(n) expensive letters. So we may iterate on the number of them and sum up the count. If we denote j as the number of expensive letters, then we will be able to use up to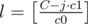 of the cheap ones. Their total count is
of the cheap ones. Their total count is 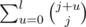 . This trivially equals to
. This trivially equals to 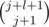 .
.
Now we know the cost of the most expensive node, we are going to use. How many such nodes are we going to use? n-count(C-1). So now we need to add all nodes, whose cost is less or equal to C-1.
Once again we iterate over the number of expensive nodes j. For taking all the nodes with cost up to C-1 we will have to pay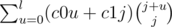 . Probably we may stop at this sum, if we are satisfied with linear solution. To get a fast solution we have to sum it up. After some transformation it may be reduced to
. Probably we may stop at this sum, if we are satisfied with linear solution. To get a fast solution we have to sum it up. After some transformation it may be reduced to 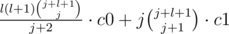
20620974 implements this solution with complexity O(log^2(n) log(n c0) ).
Awesome solution!By the way,I think this solution is a little bit similar with this:GCJ2014 FINAL D
Can someone tell me how to solve I ?
Problem A in http://www.bubblecup.org/Content/Media/Booklet2016.pdf