What is the best for Dijkstra's algorithm: set with erasing of the vertices adjacent to the current one and the subsequent insertion of them with the new values or a priority_queue with a lot of irrelevant vertices? Or maybe some other approach using std?
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3690 |
| 2 | jiangly | 3647 |
| 3 | Benq | 3581 |
| 4 | orzdevinwang | 3570 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | Radewoosh | 3509 |
| 8 | ecnerwala | 3486 |
| 9 | jqdai0815 | 3474 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 165 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 160 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | orz | 146 |
| 8 | SecondThread | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: May/01/2024 15:48:33 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I remember in an article on Topcoder about STL (you can google it easily, part 2), they are said to not differ much in terms of performance, only by 0.1% in practice.
Dijkstra with set, in my opinion, is clearer to code.
How did you measure that?
Try solving this with
std::set.I didn't manage to succeed even though I'm pretty sure my code is optimal enough,
std::setis slower thanstd::priority_queueby more that 30 times on this specific task.I have also submitted 20C - Dijkstra? more than 30 times with using many different data structures, so I guess that priority_queue is WAY faster than
std::set, at least like 2-3 times, but sometimes this advantage can be up to 20-30 times on some specific graphs.The only drawback I've seen so far is that the memory consumed by this Dijkstra is not O(N) but is O(M).
The task from main (sums) could be solved without Dijkstra, in a linear way. You're always adding edges as a kind of a cycle. For this specific problem, set might be slower but I've heard that it's better in general.
This might be because when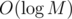 . It might be slower for graphs where M is several orders greater than N.
. It might be slower for graphs where M is several orders greater than N.
priority_queueallocates O(M) memory it will work inBut isn't it that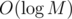 =
= 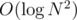 =
= 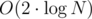 ?
?
This should be some sort of weird task where N2 ≤ M, and for shortest-path problem we can ignore multiple edges, so most of these problems will still work in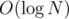
Usually in tasks you see something like 1 ≤ N, M ≤ 105 so, I believe, in general it is better to use
priority_queue.You are mixing apples and oranges.
First of all, if you use Dijkstra to solve Sums from MAIN, you should use an O(n^2) implementation, because it is a dense graph. The set/priority_queue implementations are both O(n^2 log n) for dense graphs. The log n overhead is unnecessary.
Benchmarking set vs. priority queue on dense graphs is pointless, as you shouldn't use either data structure in that setting.
Second, you are probably doing something wrong/suboptimal in your Sums implementation. I just submitted an O(n^2 log n) solution using Dijkstra with a set for Sums and got 100 points.
Finally, regarding the big picture: For sparse graphs I've seen a lot of benchmarks. The exact results of this comparison depended on way too many factors, such as the platform, compiler version, and optimization flags used. Still, the result was always (that I remember) that the runtime of one implementation was within twice the runtime of the other. In terms of programming contests (and also in terms of real life) a factor of two is negligible. I would never use the words "much faster" in this context.
Feel free to choose the implementation you like better, in the tasks when using either is appropriate.
off the topic but i wanted to know how to solve the above problem in linear way. I don't know how to approach the problem. Even a little hint would be very helpful.
This is the infamous article where I learn STL, I do not do any measurement but I think there is no reason I should not believe in this great post
UPD: Just now I've realized that it doesn't make any sense since the Dijkstra algorithm should use the set/priority_queue to get the minimum element and the unordered_set does not give us that.
From my experience, priority_queue is much faster, maybe 2x faster than set.
http://codeforces.com/contest/20/status/C?order=BY_CONSUMED_TIME_ASC
A friend of mine has made such "comparisons" as well. You know what? The results were different :D
This is all really weird.)
I tested Dijkstra's speed on this problem on spoj. ( spoj.com/problems/TSHPATH )
As per the results: Set: 1.51 seconds while Priority Queue: 0.98 seconds.
In my opinion too, priority queue is much faster than set.
Correct me if im wrong but priority queue is basically a heap so we get the min element in O(1) whereas set is a balanced bst so extract min is a O(logn) operation
Yes, you are wrong. In a heap you can find the minimum in O(1), but you then need O(log(heap_size)) anyway if you want to remove (pop) it from the heap. Which, in Dijkstra's algorithm, you do need.
Sometimes
setis faster thanpriority_queuebecausepriority_queueincludes extra set of vertices which makes my code lengthy.This submissionI don't know much coz i'm a beginner, i always used priority_queue for dijkshtra purpose but today used set for the below problem related to dijkshtra.
i found set took 4 seconds whereas Priority_queue implementation took 6 seconds.
what i concluded is Use set for sparse data when most of the valus are repeating or null(0) otherwise use priority_queue(note: std:p_queue is max heap , so pass negative distance for appropriate shortest cost and again negate it when retriving distances fom it)
Question link is here Synchronomous shopping Hackerrank
Firstly, why do you necropost that have already answers
You should put your long code into the spoiler (else it causes lag and makes people annoy)
Am I right that priority queue can sometimes give wrong answers?
reference — Problem from IOI 2011 "Crocodile's Underground City":
WA with pq AC with set
Can anybody explain this, please?