Div2 A. You can just output "0 0 n".
Author is Alex_KPR .
Div2 B. You should check for every circle of one ring: it have intersections with another ring or not. So, there are 4 checks.
There are 2 cases:
1. circle is inside of ring;
2. circle is outside of ring and ring is outside of circle;
3. circle is outside of ring and ring is inside of circle.
If at least one of these cases is performed, circle is good.
You can easily do checks following way. Let us d be a distance between centers of ring and circle, r1 and R1 are inside and outside radii of ring, r be radius of circle. Then conditions for all cases will be
1. d + r ≤ r1.
2. r + R1 ≤ d.
3. d + R1 ≤ r.
You can check all conditions in integers using squares of distances.
Author is Alex_KPR
Div2 C. Div1 A.
The first solution. Consider sequence a0 = 1, ai = ai - 1k + b:
a0, a1, a2, ..., an = z.
You can see that for all numbers from segment [a0, a1 - 1] you can number not less than z using exactly n steps. But for n - 1 steps you will bet number less than z. It works because transformation is monotonous. Analogically, for numbers from segments [a1, a2 - 1], [a2, a3 - 1], etc, you need exactly n - 1, n - 2, etc steps. So you just need find segment that contains number t. You can do it by generate a few first members of the sequence a. You need no more than t members.
The second solution. Equation:
tkx + b(kx - 1 + kx - 2... + 1) ≥ kn + b(kx - 1 + kx - 2... + 1)
Using formula for geometric progression you can get: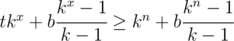
For k ≠ 1 we can multiply both sides by k - 1, (you can consider case k = 1 by yourself).
t(k - 1)kx + bkx - b ≥ (k - 1)kn + bkn - b
kx(t(k - 1) + b) ≥ kn(k - 1 + b)
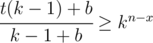
So, you can find value n - x using simply raising to a power.
Authors are Gerald and Ripatti
Div2 D. Div1 B. You should construct graph where vertices are areas of walls and edges are actions of ninja. Then you should run BFS with one modification: is you reach vertex later then water, you shouldn't do moves from this vertex.
It is solution in O(n).
Author is Ripatti
Div2 E. Div1 C. If you can reach the planet in time t, you also can reach one in any time greater then t (you can just reach planet in time t and then move along with planet). There exists some t0 for that for all t > t0 you can reach planet, and for all t < t0 you cannot do in. Let us find t0 using binary search.
Checking every of t inside of binary search you can do following way. You should calculate place if planet after time t and find distance between ship's place and new planet place.
So, you have following "classic" problem: there are two points A and B and circle with center in O and radius R (points are outside of circle), you need find distance between points and you cannot moving inside of circle.
There are 2 cases:
1. You can move direct way
2. You should skirt the circle
The second case is performed iff two following conditions are performed:
a. Angles OAB and OBA are acute
b. Height OH of triangle OAB less than R
All checks you can do in integers.
Well, let's understand how to precess our cases:
1. Obviously
2. Let us C and D be tangency points (i.e. you are moving along line ACDB). Thiangles OAC and OBD are right and you can easily calculate all angles inside of them. Then you should find angle COD. After that you can find length of line ACDB. You can see that you don't need find places of points C and D.
Author is Ripatti
Div1 D. We will construct solution recursively. For every k it is possible construct parallelepiped k × k × (k + 1) that contains 2 cubes k × k × k. For k = 2 solution is obliviousо. How to build solutions for k > 2 is shown in following picture:
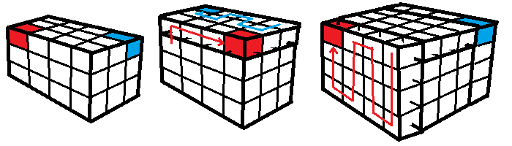
Red and blue cubes are start and end of chain. Firstly you should build one floor over. Then you should build 2 layers on two opposite sides.
For every n you can build parallelepiped n × n × (n + 1), and drop one layer for getting cube n × n × n.
Author is Ripatti
Div1 E. You can allocate all grippers as points on plane with coordinates (distance, mass). So, when you use some gripper, you are collecting grippers inside some rectangle with corner in origin. Let us collect grippers and put them into queue. For current gripper you should take all grippers from rectangle and store them into queue. Then you should take next gripper from queue and do some manipulations with them and so on. Well, now you need do it fast.
Let us create segment tree (for example, there you can use Fenwick tree) for dimention "distance". In every vertex of that tree you should store stack of points ordered by "mass". More details: every vertex of segment tree is some range of coordinates, and you should store in thet vertex points only from this range. At the top of every stack should be point with minimal mass. Well, let us put all points into tree. Every position is covered by no more thenм  segmetns, therefore all tree will require
segmetns, therefore all tree will require  of memory.
of memory.
When you process query, you should extract points from some stacks and put them into queue. You can see that you may put some points into queue twice. To avoid this you should also put number of point into stack. So, when you are extracting point from stack you can check that it is the first extract using some array of flags.
This solution works in  .
.











What does cout<<0<<0 print in prob A div 2.Please explain.
InputThe input contains of a single integer n (0 ≤ n < 10^9) — the number that should be represented by the rules described above. It is guaranteed that n is a Fibonacci number.n is Fibonacci number =)because N is definitely a fibonacci number, and so is 0, so 0+0+n always works
I think it's obvious that problems 1D and 1E should've been in other order.
Sorry to interrupt, but can problem 1E use priority_queue?
I solved the Div1. B running DFS And i think there's a problem with my code and the algorithm is wrong but it was accepted by the test 21324539
That's a good luck Sometimes my algorithm was correct but I got wrong answer on test >= 100 U R so lucky
In Div2 C, I am using C++14 to solve the question. I have performed the same math as given in the editorial and to find the minimum value of x, I apply log. That is x >= n-log(LHS_value)_to_base_k. I am using double as the type for x and am finally storing (long long)(ceil(x)) as the answer and printing that. However, I am running into precision issues. For example, in one testcase, x came out to be 1 but ceil(x) got evaluated as 2. When I am submitting the same logic using Java, everything is working fine. Here are the 2 submissions:- C++ — 39201368 Java — 39201512
Long double will also work.