→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 21:32:19 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Reminder! It starts in two and a half hours :)
Are you author?
There are many authors, and yes, I am one of them.
who are others can you say?
Dgleich, mislav, mtomic, stjepanp, dpaleka, nikolapintaric, Branfili, gegicmarija
How to solve the fourth problem ? (full solution)
Hint : you don't have to check paths of length more than 20 whose nodes values are more than or equal to 2 ,because 2^20 is bigger than maximum number of nodes.In general, it can be proven that any path that may be the solution should have at most one value > 1, leading to a solution based on a few DPs to find the longest paths consisting only of ones.
imagine the optimal solution is path C. C is either a single vertex or a path with at least 2 nodes then we can divide C in to two non-intersecting paths A & B. if magic of A is a / b and magic of B is c / d then magic of C is a * b / (c + d); magic of C is smaller than a / b and c / d if and only if either a = 1 or c = 1. so the C has at most 1 vertex v such than Xv > 1
Have you realised this was posted before the end of the contest?
I gave up about 30 minutes before the end of the contest ..
I'm really sorry, but when I realized that this could be cheating I wasn't able to delete my comment.
So what's the solution to E or F?
40% for E seems pretty trivial...but the rest of the problem seems really hard!
I am the author of problem E.
The key observation is this: there always exist a dwarf which can never be passed, that is, it's impossible for an elf to walk up to that dwarf and see he is occupied. There can be more than one such dwarf, but we only need to find one. Let Pi be the number of elves whose initial adversary has an index less than or equal to i. We will take the smallest of all the values Pi - i, let that be at position k. Than it is impossible for a dwarf to pass from position k to k + 1.
Now, we simply take k + 1 as a start, and do a greedy algorithm from that starting point.
Here's what I did for E (I'm not sure if it's correct, but it seemed intuitive):
Consider the 40% subtask. Go through each dwarf starting from the first one. At each point, the choice for an optimal solution is uniquely defined (didn't prove it, but seems intuitively correct):
This can be extended to the full solution. First, because we have exactly N elves, there is always at least one point i where the elves will not "spill over"; that is, no elf will ever come from dwarf i - 1 to i (or from N to 1 if i = 1). This is the critical observation.
For example, if N = 6 and there are 3 elves assigned to dwarf 3 and 3 elves assigned to dwarf 5, then the point where the elves will never spill over is 3: because, an elf can never come from dwarf 2 to dwarf 3.
Hence, we can relabel all the dwarves, shifting their labels such that i = 1. Now we just perform the same algorithm as earlier. Make a set with all unused elves who were originally assigned at dwarf 1 (relabeled), and then perform the algorithm described for the 40% subtask. When we move to a new dwarf, add all the elves assigned to that dwarf to the set.
Due to our relabeling, we will never run out of elves at any point. Also, we can be sure that no elves can come from dwarf N to dwarf 1 by definition, so we don't have to worry about that.
If anyone can come up with a counterexample to this solution, please let me know :)
EDIT: It seems like this is the same as the author's solution. haha :)
Yes, that is exactly the same as my solution, and explained in more detail :)
Not sure if this is correct but..
F: Bitmask dp. dp[S] is the answer for set of strings S. Once you have computed answer for all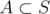 you can compute dp[S] by first computing the size of the maximum common prefix for the strings in S (including the root node), (for example the maximum prefix for {aabbc, cab, cca} is 3 ("ca" + root)) and then taking
you can compute dp[S] by first computing the size of the maximum common prefix for the strings in S (including the root node), (for example the maximum prefix for {aabbc, cab, cca} is 3 ("ca" + root)) and then taking  .
.
The idea should work because we can construct any optimal trie by using merge of two different tries that only share the maximum common prefix.
It's correct.
Are there any problems with grading system? Will this COCI be unofficial?
My code for problem F was TLE but, I downloaded the tests and run in my computer, it was half of time limit. So funny ...
When will be the editorial published?