Let's discuss the solutions of all the problems. I would like to know other peoples approaches for the problems. This time I am only able to solve Problem A. What are your views about the problems ?
Here are the problem statements.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Let's discuss the solutions of all the problems. I would like to know other peoples approaches for the problems. This time I am only able to solve Problem A. What are your views about the problems ?
Here are the problem statements.
| Name |
|---|



Problem A:
len is length of S.
let count(k) be the number of blue bulbs in range [1, k].
then the answer is count(J) — count(I — 1).
count(k) = count(k % len) + (k / len) * count(len)
for k <= len, we can store the answer in a table.
time complexity O(len)
EDIT1: Here is the AC code. I have completely avoided overflows as I find f(b) ≥ 0 or not cleverly.(Not using log but finding the GP sum in O(log(VAL)) and returning when sum reaches ≥ 1018
For Problem B, for given number N, you need to find the smallest number b such that there exists some x so that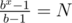 . Iterate x from 64 to 2 inclusive, and binary search for value of b.
. Iterate x from 64 to 2 inclusive, and binary search for value of b.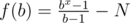 . This will be an non-decreasing function. So binary search for the value of b that makes it 0.
. This will be an non-decreasing function. So binary search for the value of b that makes it 0.
Consider
*Warning: Beware of overflows. See implementation above.
Why is x from [2,18] ? Suppose , for N=1125899906842623 , the value of x should be 50 for b=2. Please correct me if I'm mistaken. I did the same thing as you explained where x iterated from [2,70]. Although I was getting overflow for the large inputs. Can you please elaborate on how to solve it using log.
Why would be x from [2, 18]? You are right. It won't be. It would be from [2, 64].
Regarding usage of log:
You know you are in trouble when bx is very lagre or (b - 1) * N is very large. How to check whether x * y ≥ 1018? Simple log(x) + log(y) ≥ 18. So whenever you are in trouble, you know that result is very large. So you can use log(x) = log(x + 1).
Finally checking whether f(b) is > or < 0 becomes easy when integer overflow is occurring. You need to check sign of (log(bx - 1) - log(N) - log(b - 1)).
we can avoid using log, we can just iterate for all the bases within 106 upto all powers such that highest power is less than 1018 , Now if the base is bigger than 106 then then number n must have less than 3 bits in its representation .Now we just have to check if 1 +x +x2 = n . This is equivalent to saying that n-1 is product of 2 consecutive numbers , which we can easily check . Also if we need to check x*y>1018, we can check without using log using this : x >= 1018 / y.
"upto all powers such that highest power is less than 1018?" I don't think so because limit on bx is N * (b - 1) and N itself can be 1018.
For product of two no's, yes you are right.
we'll keep adding along the powers to form the possible numbers . hence although the limit on bx is N * (b - 1) but on the whole number n the limit is 1018 ,we only need to check the highest power less than 1018
Yup I don't think you need to use log. I have provided a function below that will generate all the numbers that can be represented by a particular base.
Seems you are right. I have updated the post and attached the code.
Hey, Could you link me to your program?
I'm not sure how to implement the binary search as well as how to handle large numbers.(I did read your other comment,but I'm still not sure)
You can see it here.
I somehow managed to pass small but not large in B, and I had already taken care of overflow but it seems that overflow is the only possible issue.
I coded something like this: http://pastebin.com/8Y33HnTZ
and handle if cnt != bit_length (ie sz) and tt != x. No idea where did I fuck up.
Hey rachit, I used the same technique as yours in contest but is failing for large case Could you please see what is the problem in this code — https://paste.ubuntu.com/23440777/
Yes. I have updated your code. Problem was in expo function. :)
Thanks very much, made very silly mistake :(
for length x, we need to find b satisfy the condition, for N , the most significant bit is b^(x — 1), b is the only one could be result, so, we can get it by b = pow(N, 1.0 / (x — 1)), if b > 1,then we just need to check whether length x of base of b is the ans. i learn it from hdu_toraoh.sorry for my poor english.
Problem B:
just iterator over B and nr_digit is also fine...
trick : use a multiprecision library to deal with large integer, like boost::multiprecision::mpz_int. It's allowed in codejam.
UPD: It's wrong. I didn't remember it clearly until I looked at my code... see comments below.
This is what I was doing but it didn't give a solution to a single test case in 3-4 minutes.
I'm wrong. I iterator over nr_digit first, then binary search for B.
So I did the same thing as rachitiitr.
link to my code http://ideone.com/pSMiap
many tricks...
Problem C: count the number of tuple (a, b, c, x) s.t.
(1) D divides x
(2) a >= 1, b >= 0, c >= 0
(3) a * x + b * (x + 1) + c * (x + 2) == N
time complexity O(N / D * N), but you have 4min to solve the problem. it's enough...
What would be the solution for the large input?
This is the solution to the large input.
It takes me about 10 seconds to process the large input.
A program that executes 10^11 instructions is acceptable in Google codejam.
I tried implementing what you said but its taking very long.
I think I am doing this part wrong:
count number of (b, c) by solving indefinite equationCould you show me your code or tell me the correct way of counting?
Sorry if its a dumb question.
For this problem, we need to find (b, c) s.t.
b * (x + 1) + c * (x + 2) = Rbecause
-(x + 3) * (x + 1) + (x + 2) * (x + 2) = 1.a solution is
(b, c) = (R * (-x-3), R * (x + 2))all solutions are
(b, c) = (R * (-x-3) + k * (x + 2), R * (x + 2) - k * (x + 1))the number of solutions is the number of k that makes b >= 0 && c >= 0.
This link may be usefull : http://math.stackexchange.com/questions/20717/how-to-find-solutions-of-linear-diophantine-ax-by-c
Generally, we can get initial solution and incremental of it by extended Euclid algorithm.
Thanks a lot! Finally got AC and more importantly, learnt something very useful and important today!
Here's an O(NT) solution.
iterate through the possible amount of buckets from 1 to floor(N/D)
calculate the amount of balls on the leftmost bucket, this is fixed unless D=1, which could be handled by considering two values for the leftmost bucket.
Note that we only care about the amount of bucket that has the same amount of balls with the leftmost one. This is because the sequence is non-decreasing and maximum difference is two so there is only one partition method for each amount of buckets that shares the same value with the leftmost one.
Code: http://pastebin.com/G5Mmzfdw
It's a very insightful observation.
x is fixed can be proved in another way.
(a + b + c) x <= (a + b + c) x + b + 2 c < (a + b + c)(x + 2)
then
N / (a + b + c) -2 <= x < N / (a + b + c)
so the range of x under fixed (a + b + c) is at most 2. x is fixed if D > 1.
Thanks ! That helped a lot !
I did not look at your code because I want to understand it conceptually first. So basically in addendum to Georeth's formulation, you are fixing a first right ? Conceptually how is this fixing b and c or the number of valid b and c ?
This is because I have also fixed [a+b+c] (the total amount of buckets). Therefore if I also fix [a], [b+c] is fixed. That will form a system of two unknowns with two variables, and obviously that will result in only one valid answer set. Also, since the range of [b+c] is continuous, the range of [a] is also continuous and we can make use of this to calculate the range of [a] and the total amount of valid answers in O(1).
Woah! That was a very elegant way of doing this !
Ikr, I wouldn't have thought of this hadn't I misread the statement as solving the question for given N,D and fixed bucket amount. =]
I couldn't solve Problem D, but was trying in the following way.
When P = 2,
Observation: We are given a permutation of 1....N. We need to make it sorted.
If array is sorted answer would be N.
Otherwise if answer exists, then there would be 2 sub-arrays [L1, R1] and [L2, R2] such that
SubArray[1, L1 - 1] will contain all the numbers from 1 upto L1 - 1.
SubArray[L1, R1] would contain R1 - L1 + 1 consecutive elements with range [L2, L2 + R1 - L1].
SubArray[R1 + 1, L2 - 1] would contain consecutive elements with range [R2 - L2 + L1 + 1, L2 - 1].
SubArray[L2, R2] would contain consecutive elements with range [L1, R2 - L2 + L1].
SubArray[R2 + 1, N] would contain consecutive elements with range [L2 + R1 - L1 + 1, N].
I have not considered edge cases where L1 = 1 or R2 = N etc. Once I get the corresponding L2, R2 for given L1, R1 answer would be max(answer, 2 + dp[1][L1 - 1] + dp[R1 + 1][L2 - 1] + dp[R2 + 1][N]) where dp[i][j] is the maximum number of partitions of SubArray [i, j] so that when you sort those partitions , SubArray [i, j] also gets sorted.
Would be glad if someone could help what to do next.
UPD 1: Here is the code. To check for subarray [i, j] to have j - i + 1 consecutive elements, you can simply check max[i][j] - min[i][j] = j - i.
P = 3 is hard.
Does anyone have a code for large case P = 3? Thanks!
I got passed finally (Solution)
For the large version of problem B just check for all divisors of (n-1). It worked well for me.