Topcoder SRM 709
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/27/2024 07:00:32 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Contest will start in 18 hours.
Who can register for Humblefool Cup?
Anyone who is affiliated to any university can register. Link is below: https://aparoksha.iiita.ac.in/humblefoolcup/Register/
and for more information : Click here
In div1-easy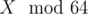 we indeed want to maximize X.
we indeed want to maximize X.
dp[1<<n]doesn't work because sometimes smaller X can give bigger answer later. The solution is to computedp[64][1<<n]: for each mask of last 6 bits of X what is the biggest possible X. It can be proved that for the same value ofIn div1-med for each already fixed prefix (we fix whether letters are lowercase or uppercase) of
Swe care only about the number of occurrences so far and about some last letters. In detail, it's enough to know the longest already-matched prefix of one of patterns. For example, if we know that suffix of already fixed letters allow us to match first 5 letters from pattern 1 and 17 first letters from pattern 2, we can just remember that we match 17 letters from pattern 2: then we know how to fix letters (that info implies which of 17 last letters should be uppercase) and thus we know all shorter matches of prefixes of patterns. So we can doint dp[N][K][N]— for each prefix and each possible pair (which_pattern, matched_prefix_length) we need the maximum total number of occurrences so far. The complexity of this solution is O(N4·K2) but there are some faster approaches.For div1-med, I had N^3 * K time complexity. For a pattern and a starting position, we get a unique string of 0s and 1s (1 is if you shift the letter, 0 if you let it be the same). So we get N*K such strings. We push them all in the same trie and use the same automaton that aho-corasick generates because at each step you are interesting just in this kind of substrings, and, more exactly, in the prefixes of such substrings. So we have (N * K) * N states and we multiply it by N by applying the transitions of such states through the built automaton. I guess the idea was just to get a polynomial solution but I chose to explain this one too for anyone interested in a better complexity. The contest was nice and I'm really interested in the solution for div1Hard (I had a 2^(N / 2) * N complexity by keeping at each step the configuration of already fixed brackets that may influence your further decisions, so we actually keep the state of at most min (i, N-i) <= N / 2 brackets). If you are the author of the contest, could you explain this problem too?
Nice solution ;)
I was a tester and I don't know anything about Hard. It was some old problem waiting to be used. cgy4ever should know who an author is (maybe he is).
subscriber created other problems and I think that his div1-easy was awesome.
Can you explain a little more about why we only need to work with the last 6 bits?
In a formula X = X + (X ^ Ai) only last 6 bits of X are affected by xoring because Ai ≤ 50 < 64. The other part of X is just multiplied by 2. Let's see an example.
X = 1011010100 and Ai = 101111. Then X ^ Ai = 1011111011 so X will become 1011010100 + 1011111011 = 2 * 1011000000 + 010100 + 111011. Since the bolded part is just doubled, the bigger it is, the bigger new value of X will be.
Understood now. Thank you so much for the explanation :)
Div2-hard anyone?
O(N4) dp. The state is dp[position in our string of letters][longest prefix of the pattern that we can cover]. In each state we have two options — to continue our pattern or to not continue. If we decide to continue we just increase the position in the pattern and in the string. If we decide to break the pattern we compute the new prefix which we can cover. The finding of the new prefix can be done in O(N2) and so the total complexity will be O(N4).
Would you mind posting a snippet of code?
O(n3) solution
dp[i] -> max occurences with a valid entry ending at position i
now for each j < i check if possilble that valid string ended at j and if there is any overlap for string ending at i and j if that overlap is valid or not . If its valid
dp[i] = max(dp[i],dp[j]+1)
Solution
How to solve Div2 500 ?
For every connected component find number of edges in it, denote it as x. Also denote number of vertices in a graph as n.
If x = n * (n — 1) / 2 && x % 2 == 1 -> return -1, since the graph is a clique, we can't add any edge to make the count even.
If not, increment oddCount or evenCount depending on parity of x. Return oddCount.
Could you, please, attach a link to your code?
http://pastebin.com/deigawAD Sorry for the delay!
answer will be the number of components which have odd number of edges
except when it is only one component and it has odd number of edges and E = V*(V-1)/2 ans will equal -1
Am I the only one who is finding very difficult in understanding problem statements — Particularly Div-2 250 pointer in today's SRM and Div-2 500 pointer in Round-398.
How to solve Hard? I tried to use very easy solution that works in (branch on all possibilities of colors with frequency >=2 and do dp on alone ones) with a lot of optimizations, but it works just a bit too slow, if TL had been 2s then I think it would have passed. But I guess this is not model solution :P.
(branch on all possibilities of colors with frequency >=2 and do dp on alone ones) with a lot of optimizations, but it works just a bit too slow, if TL had been 2s then I think it would have passed. But I guess this is not model solution :P.
Divide the sequence into two parts. You need left_bal = -right_bal >= 0. Fix all the colors that are both in the left and the right parts. After that use meet in the middle. That would be 2^(n/2) * n.
Now you need to optimize it a little bit (I was scared). When I was choosing colors from both halves at the same time I was checking that current summary balance could get to 0 if we just use all left numbers. For example, if you have ~25 colors contained in both parts, then if there would be too many open brackets within these ~25 multicolors then summary balance would be greater 0 no matter what.
You could read my code for better understanding.
I got AC with the solution you described. I branched from the colors in the order of their first occurrence and my only heuristics were checking that all of the prefix sums can still be non-negative and that all of the suffix sums can still be non-positive.
An O(2n / 2) solution is kinda possible. Do a recursive search on the first half of the sequence, maintaining two integers -- the balance of this half and the mask of the bracket types for colors present in both halves. Save these pairs of integers in a hash table. Then do the same for the right half, this time searching the hash table instead of adding into it.
If the memory limit was 1GB, the same solution would be possible without the hash table -- there are 224·13 possible pairs (mask, balance). I went for that, while dividing the sequence in 22:28 ratio -- then you need 222·12 ints, which fits into 256MB. This "unequal division" caused a couple of bugs in my code, but my solution in the practice room passes systest in 250ms.
I also thought about this 1GB, but I decided to use memory of 13 bytes, not 2^n/2 * 13. To do that you could at first fix colors contained in both parts. This would cause asymptotics to become 2^(n/2) * n in case when all the colors are in both parts. So I made some optimize for that case.
Now I see that rng_58's solution in the practice room is more clever. For every balance, he saves the masks of the left and right parts into separate vectors. Then, for counting the pairs of equal masks in vectors corresponding to the same balance, he uses a single array of size 225.
This solution works in O(2n / 2) and uses O(2n / 2) memory.
Cool!
It works in 400ms. My solution during the contest (push all pairs into a single vector, sort it, and do two-pointers) was 900ms and I was quite unsure.
It can be a general technique. Suppose that we have two arrays a[0], ..., a[N - 1] and b[0], ..., b[N - 1], where each element is up to M. We want to compute the number of pairs (i, j) such that a[i] = b[j]. Let X = sqrt(M). The following works:
Both time and memory are O(N + sqrt(M)).
I think the solution you describe is actually O(2**n/2). Note that the DP runs in O(num_singles**2), not in O(n**2). In case we have 25 pairs, we have 0 singles.
Practically it passed in 900ms in practice room, though, so apparently I have too much overhead.
Actually, I implemented DP in O(n^2) ;). I am not very smart to miss this, but I think achieving O(alone2) is pretty technical to implement, O(n·alone) is very easy and that should already make my solution much faster, I will investigate it if I have some time.
However I implemented some rules about when to completely disregard DP phase and cut backtrack, so I think my solution is better in terms of complexity than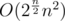 . If I have 25 pairs I still use O(n2) for every DP, but I only perform it if they form correct parentheses sequence, so that number is for sure much smaller than
. If I have 25 pairs I still use O(n2) for every DP, but I only perform it if they form correct parentheses sequence, so that number is for sure much smaller than 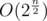 , but it is not obvious how to bound it simply by Catalan number (which is
, but it is not obvious how to bound it simply by Catalan number (which is 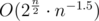 ) or something similar.
) or something similar.
Here's a formulation that I believe makes O(alone**2) easy: a parentheses sequence is balanced if and only if: 1) each prefix of size 2k-1 has at least k opening parentheses 2) in total it has n opening parentheses
These conditions easily translate into conditions on the number of opening parentheses in various prefixes of "alone" points subsequence.
Although you're right that my solution also filters out impossible combinations before even starting a DP (which is also convenient to do in the above formulation: just need to check that we don't have more than n opening parentheses in total, and that for each prefix its lower limit doesn't exceed its size), and that contributes a lot to lowering the running time.
I tried to count the complexity (code: http://ideone.com/YYB29V ), it turns out to be this: https://oeis.org/A036256. So it is O(2n / 2 * n - 0.5) (time and memory).
This was my second and last contest on Topcoder. The website is extremely slow and messy. I clicked to open problem but it took minutes to open and even after that some of parts of problem statement were missing, like method signature and parameters.I refreshed the page and it again took minutes to load. In between, people were submitting for 250 points. I felt very irritated and performed too bad.

Nobody cares.
Don't use the website. Use the applet which is supported from dozens of years back.
Does Topcoder have editorials anymore? I could just fine this: https://apps.topcoder.com/wiki/display/tc/Algorithm+Problem+Set+Analysis, but this seems to be updated very late and editorials for a few SRMs seem to be missing. Is anyone aware of any other source?
Unfortunately those editorials are created a long time after a round.
Codeforces is the only other source. For recent SRM's you can just go through cgy4ever's blogs. There is sometimes a discussion about problems or even a short editorial from an author.
Oh okay. Thanks!
Thanks for problem setters and testers! The d1-easy and d1-hard problems were interesting. What is intended solution for hard? After contest, I solved it with meet-in-the-middle approach. Is it intended?
Yes, it is the intended solution.
The D1-Easy is a very interesting problem to me because when I tried to come up with recursive memoization formulation I failed at doing so / found it quite difficult to think about, however after trying the iterative DP it was quite simple. Typically I always find recursive memoization much easier to think about so it is a strange feeling, does anybody know if there is a specific type of DP problems for which iterative solutions are much simpler? Is there a certain property of this problem that makes it seem this way to me?
I find that in case when you know for example in dp[i][j][k] that i will increase in each step it's better to use iterative approach with i in main for (if i increases by 1 you also can save memory). But for example in case where sum (or more complicated order) of i, j, k should increase/decrease I'd prefer to use recursion.