have been trying this question which requires below work done.
PROBLEM
Given an integer n which signifies a sequence of n numbers from {0,1,2,3,4,5.......n-2,n-1}
We are provided m ranges in form of (L,R) such that (0<=L<=n-1)(0<=R<=n-1)
if(L <= R) (L,R) signifies numbers {L,L+1,L+2,L+3.......R-1,R} from above sequence
else (L,R) signifies numbers {R,R+1,R+2,.......n-2,n-1} & {0,1,2,3....L-1,L} ie numbers wrap around
example
n = 5 ie {0,1,2,3,4}
(0,3) signifies {0,1,2,3}
(3,0) signifies {3,4,0}
(3,2) signifies {3,4,0,1,2}Now we have to select ONE (only one) number from each range without repeating any selection. We have to tell is it possible to select one number from each(and every) range without repetition.
Example test case
n = 5// numbers {0,1,2,3,4}
// ranges m in number //
0 0 ie {0}
1 2 ie {1,2}
2 3 ie {2,3}
4 4 ie {4}
4 0 ie {4,0}
Answer is "NO" it's not possible.Because we cannot select any number from range 4 0 because if we select 4 from it we could not be able to select from range 4 4 and if select 0 from it we would not be able to select from 0 0
My approaches -
1) it can be done in O(N*M) using recurrsion checking all possibilitie of selection from each range and side by side using hash map to record our selections.
2) I was trying it in order n or m ie linear order .Problem lack editorial explanation .Only a code is mentioned in the editorial without comments and explanation . I m not able to get the code
I am not able to understand the logic/algo used in the code and why is it working?
Please suggest ANY linear method and logic behind it because problem has these constraints
1 <= N<= 10^9 1 <= M <= 10^5 0 <= L, R < N
which demands a linear or nlogn solution as i guess??
The code in the editorial can also be seen here http://ideone.com/5Xb6xw
Warning --After looking The code I found the code is using n and m interchangebly So i would like to mention the input format for the problem.
INPUT FORMAT
The first line contains test cases, tc, followed by two integers N,M- the first one depicting the number of countries on the globe, the second one depicting the number of ranges his girlfriend has given him. After which, the next M lines will have two integers describing the range, X and Y. If (X <= Y), then range covers countries [X,X+1... Y] else range covers [X,X+1,.... N-1,0,1..., Y].
Output Format
Print "YES" if it is possible to do so, print "NO", if it is not.











Okay, so the first step should be to solve the problem where the intervals cannot wrap around (it is common for problems with/without wrapping around intervals to have very similar solutions), so I will go over that first:
First of all, consider the easy case when all start points are distinct. Then, you can just pick all of the start points and you are done.
Now, a lot of times when you are solving problems of this kind, you will want to select the set of numbers of your answer in increasing order and choose the interval for each one as you go (think of it as moving left to right over a number line and picking up the numbers in your answer as you go). Of course, this will involve reordering the intervals so that the smallest number you choose is actually in the first interval, the second number you choose is in the second interval, and so on. Going back to that easy case, you can just sort the intervals by start point, and this will hold true. This gives you an easy algorithm when the start points are distinct that will give you your list of numbers in increasing order:
Now, what cases make this algorithm not work? The cases when you have multiple intervals with the same start point, of course! So, let's look at a case like that (after sorting by start point):
1 4
1 2
1 1
4 4
Now, just placing them at the start points won't work, so we need to consider other options. So let's add in the following: If we have already used the start point, let's instead add our last number + 1 and hope it's actually in the interval. This is allowed since we are placing numbers in order so we won't have placed anything bigger than our most recent number yet.
So, our list will be: 1 in [1, 4], 2 in [1, 2], 3 in [1, 1], and 4 in [4, 4]. Unfortunately, this is not correct, since 3 is not in [1, 1]. So how can we do better? Well, if you look at the group of intervals that start with 1, we will put the smaller numbers in the intervals that come earlier, so let's put the intervals that end earlier first. In other words, we will not only sort by start point, but will break ties by sorting in increasing order of end point. So, our list of intervals will look like this with the new sorting:
1 1
1 2
1 4
4 4
Let's try that algorithm again with the new sorting and see what we get: 1 in [1, 1], 2 in [1, 2], 3 in [1, 4], and 4 in [4, 4]. And it worked! The algorithm will look like this:
But wait! What about a case like this?
1 1
1 5
1 6
2 2
Here, we will assign 1 to [1, 1], 2 to [1, 5], 3 to [1, 6], and 4 to [2, 2], which is wrong, but if we gave the 2 to [2, 2] it would have worked. So once we use up a certain number x, we need to start considering all intervals that start with x + 1, and always take the one with the lowest endpoint. We will need a priority queue for this!
Now for the case where the intervals can wrap around! To do that, we will use a very similar process. However, we have to handle the wrapping around somehow. A common technique for this is to consider the range from [0, 2n] instead of [0, n], duplicating our range of possible values. Now, intervals [a, b] that do not wrap around can be treated as both [a, b] and [a+n, b+n], and intervals that do wrap around can be treated as [a, b+n]. Now, the problem is the same thing as before, but we have to satisfy both intervals for the no-wrapping-around case. Note that we might use a different number to satisfy the two intervals that mean the same thing. For example, consider the case below for n = 4:
1 2 2 3 4 1 4 2
Our intervals will be [1, 2], [5, 6], [2, 3], [6, 7], [4, 5], and [4, 6]. Then the algorithm above gives us the solution: 1 for [1, 2], 2 for [2, 3], 4 for [4, 5], 5 for [4, 6], 6 for [5, 6], and 7 for [6, 7]. However, this tells us that we used 1 to satisfy [1, 2], but to satisfy its duplicate interval [5, 6], we used 6, which corresponds to 2 (because it is 2 + n). So which one did we use? It turns out that we can shift our early answers to be 2 for [1, 2] and 3 for [2, 3], and this makes our solution consistent. This will always be possible to do if we find a solution for the problem with both copies of the intervals added in, though I won't go over how to extract the list of numbers (since it's quite a bit more complicated and not a part of this problem). But for this problem, just modify/duplicate the intervals as described and apply the greedy algorithm with the priority queue that I described at the end of the no-wrap-around case above, and this should tell you whether or not it is possible.
too slow :-(
Firstly, let's only consider the queries when L <= R. For a given set of intervals starting at the same point, it can be proved that if there exists a solution, then there is one in which the selected value for the interval having a lower R value will be smaller that the values selected for the others intervals. This is precisely the solution that we will build.
After processing all the elements in the list you will have a solution for the problem. Note that if in some point while performing step 2 you find that the L value of the interval is greater that its R value, then the problem doesn't have any solution.
In order to handle the queries when L > R, let's transform the problem in other equivalent to it, using a widely used technique consisting in duplicating the input range. Instead of having the range (0, n -1), we will have the range (0, 2 * n — 1), and the queries will be transformed in the following way. - L <= R: Transform this into two queries: (L, R) and (L + N, R + N) - L > R: Transform it into one query: (R, L + N)
Note that after this transformation all the queries have the form L <= R and the initial problem has solution iff the second one has one.
The code that you linked above efficiently implements this solution. Actually all what I did was just explain the code to you.
This is a blatant copy of GCPC 2013 problem G: Ringworld. You can get the problem set, the sample input, the secret test data, the solution outlines and some judge solutions at http://gcpc.nwerc.eu/gcpc_2013.php.
It turns out that instead of solving the original problem directly, where the segments are on a circle, we can instead solve the problem where the segments are on a line using the transformation given in the judge solution because of
magicHall's marriage theorem.First notice that if the original problem is solvable, then n ≤ m and the transformed problem is solvable. The proof of the converse is outlined below.
Using Hall's marriage theorem, it is sufficient to prove that for all subset of ranges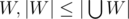 . There are two cases to consider.
. There are two cases to consider.
Case 0: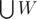 is the whole circle. In this case we just need to check that n ≤ m.
is the whole circle. In this case we just need to check that n ≤ m.
Case 1: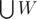 is not the whole circle. In this case we can cut the circle at some point not covered by
is not the whole circle. In this case we can cut the circle at some point not covered by 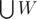 and flatten it. This does not change |W| and
and flatten it. This does not change |W| and 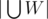 . If the transformed problem has a solution, then
. If the transformed problem has a solution, then 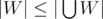 .
.
Example input for a single test case:
Consider the case where W = {[3, 0], [0, 1]}. In this case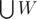 is not the whole circle. We can cut the circle at 2 and flatten W to {[3, 4], [4, 5]}.
is not the whole circle. We can cut the circle at 2 and flatten W to {[3, 4], [4, 5]}.