NAIPC is coming up on April 15 (start time here). More information can be found on the site. The contest will be on Kattis on the 15th. About 15 hours later, it will be available as an open cup round as the Grand Prix of America. Please only participate in one of them, and don't discuss problems here until after the open cup round.
The deadline to register for the contest on Kattis is April 12th. You can register by following instructions on this site: http://naipc.uchicago.edu/2017/registration.html# You will need an ICPC account to register.
You can see previous NAIPC rounds here: 2015, 2016. 2016 is also available in the codeforces gym here: http://codeforces.com/gym/101002
UPD 1: The deadline to register is in a couple of days.
UPD 2: Both contests are now over
NAIPC standings: https://naipc17.kattis.com/standings
Open Cup standings: http://opentrains.snarknews.info/~ejudge/res/res10376
I'll update this one more time with solutions once they are up.
UPD 3: Test data is available here (solutions may show up later, but I'm not sure when): http://serjudging.vanb.org/?p=1050











so,it's unrated?
How is it related to ICPC? Will North American teams be selected based on this contest?
This started as a contest for North American ICPC teams. It used to have some big prizes but since we don't have many sponsors currently, it is mostly just for fun now. It's meant as some more practice before WF, and is not used for any kind of selection.
No teams are selected from this contest this year.
North America is trying to form a super regional for WF selection sometime in the future (something like NEERC). This contest is a stepping stone to that end.
Right now the contest is a WF preparation contest. The target is an ICPC WF level set to prepare teams for the difficulty and pressure of ICPC WF. (Or that's what I've been told anyways.) It used to be an onsite invitational contest (at UChicago) for teams going to ICPC World Finals but due to lack of sponsorship in recent years is an online only contest.
Will there be a gym mirror?
Contest is over and results are .
.
How do you estimate how fast flow works?
I believe G is a flow problem. There are various ways to construct a graph, and also there are various flow algorithms. What is a good way to choose them? (Big-O analysis is not very useful here)
Distance from source to sink is rather small here, so I believe Dinic will be the best one. Network usually should be chosen such that number of edges is as small as possible. In this problem we used network with about 106 edges.
Can you describe more about your network?
Make nodes for every horizontal segment, it could be done straightforward using nm3 / 6 edges or in segment tree-like technic using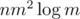 edges.
edges.
Then we made something like sparse table over each group on n segments having the same left and right ends. It cost us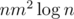 edges. Then each customer has 2 edges.
edges. Then each customer has 2 edges.
P.S. Now I realized that first part could be done like sparse table too. In that case it will consist of nm2 edges
Just sparse table (2dimensional) is enough to get 0.5 running time
I tried to create such solution, but it has more edges and its implementation looked for me more tricky.
Why? It has 2 * n * m * 5 * 5 + k * 4 + n * m edges
Sadly, the data for G was extremely weak to the point that very naive greedy solutions passed the data. This caused the Dinic to find a solution on its first iteration and simply break out very early. I have been working on generating some stronger data and have got something that takes >10 seconds. This is more than double the timelimit allotted for this problem.
Here comes the question to the authors: how did they decide to make such constraints? Why weren't there strong tests on the contest? Haven't they had a doubt when preparing the problem, that on some tests this solution might be working too long?
Initially the bounds were set at k = 1,000. However the data was weak and naive flow solutions that should TLE passed in time. Thus they raised the bounds. However, they failed to consider that the data was just weak and not that this flow graph just runs fast. (It doesn't if you make good cases)
Interestingly, for this problem, I found [Ahuja-Orlin's](http://dx.doi.org/10.1002/1520-6750(199106)38:3<413::AID-NAV3220380310>3.0.CO;2-J) variant of Edmonds-Karp algorithm faster than Dinic's (passing in 2.4s whereas Dinic's times out). See: "Distance-directed augmenting path algorithms for maximum flow and parametric maximum flow problems"
This is with a Java implementations of Ahuja-Orlin and of Dinic that are fast enough to both pass fastflow on SPOJ.
My worst case is market-1001.in with 421,200 nodes and 1,622,129 edges. I do not believe that I am building the network optimally. Could someone share how many nodes/edges you get for market-1001.min?
I can also pass using zeliboba's "straightforward" approach of using just horizontal segments, which produces 102,552 nodes and 5,105,000 edges for market-1006.in and again passes with Ahuja-Orlin only.
You want to create a 2D sparse table. This will create a smaller graph. However, the data for G is still relatively weak.
Try these cases: https://drive.google.com/open?id=0BzaDgSP3MuIGcGdvNVc5c0R3NXM
I have created 52 cases which cause even the judge solutions to TLE.
Can you describe further what you mean by "sparse table"? Are you suggesting to build a network with multiple layers for powers of 2, each representing successively smaller quadratic (2i × 2i) portion of the entire market? Analogous say to the technique to do a 2D RMQ in O(1) with precomputation?
precomputation?
Wouldn't that require up to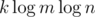 edges? In other words, would each customer's nodes be linked to the largest squares covering the customer's area?
edges? In other words, would each customer's nodes be linked to the largest squares covering the customer's area?
A normal sparse table (used in RMQ) creates log n ranges from every possible left point allowing queries eith only 2 lookups. You can do this in two dimensions by brute forcing a top left corner (do all top left corners) and then having log n widths and log m heights. This creates n*m*log n*log m different nodes in your sparse table. Then, each customer only needs to connect to 4 of these nodes to cover his entire range. You also want to be careful while creating edges from stores to your sparse table nodes. You want to do layering similar to how RMQ generstes its table. This will minimize the number of edges you need to add.
So with this approach I pass in 1s on Kattis (159,051 nodes and 615,598 edges for market-1006.in), but (a) Dinic still times out (only Ahuja/Orlin's improved shortest augmenting path passes) and (b) I still take about 14s for your additional test cases. I assume your network is immune to a bad choice of maxflow algorithm?
How do you connect layer to layer? I tried connecting using 4 edges from layer (2i, 2j) to layer (2i - 1, 2j - 1) as well as just connecting using 2 edges to (2i - 1, 2j) or (2i, 2j - 1). My (20, 20) layer are the stores themselves which are connected to the sink. I also optimized out redundant edges when a customer x or y range is a power of 2.
Are further optimizations necessary? What do you mean by "careful while creating edges"?
The data I made should hopefully make any flow solution TLE. The bounds for this problem were just way too large and it is not possible to get a flow solution to pass good data. The data on Kattis, however, is very weak and greedy solutions pass it. Thus, you will want a flow which will find some answer and break early if it realizes that answer is already optimal. As far as I knoe, some implementations of Dinic will do just that but you may just have to get lucky on its choices. Ultimately, the data is just too big and it may just not be possible to get your flow to run in time because the way youbare saying you construct the graph sounds right to me.
I see. Looks like I got it now. Here's something else I learned: for both Dinic and Push/Relabel with FIFO and Gap heuristics, it matters in which direction you construct the network. I had connected the source to the customers and the markets to the sink.
When I switched it to connect the source to the markets, both Dinic and PushRelabel passed on Kattis with less than 2s. Whereas under Ahuja/Orlin it didn't matter which direction the network was constructed. That's something I hadn't known.
FWIW, the slowest of your additional test cases is case_112 which takes about 12s on my machine.
Yeah that makes sense. And yeah I was just generating random cases with certain special bounds to make things take long. I believe there exists a case which can make a solution take >60 seconds but it is probably super hard to construct. Even then, I have cases that cause even the judge solutions to TLE with 3x-5x the alotted time.
Is there a non-flow based solution that handles the problem bounds within the time limits for the worst case?
Not that I or the judges know of. The intended solution is the flow with 2-d sparse tables.
Maybe you can try this: https://puu.sh/vInRF/c27338e52d.txt It is a O(nm) construction but after reading comments above I'm not sure about the correctness (it passes the weak test cases tho)
UPD: yep, my solution is wrong, I have no idea how it passed system test wtf
Nezzar,
The system test data was very weak. It was randomly generated in such a way that stores were given way too much stock and the customers not enough requests. Thus, it was always optimal to simply greedily assign apples to customers as they ask for them. This obviously doesn't work. However, it does indeed pass the judge data.
Apparently what happened was that the bounds were initially k=1,000. However, because of the weak data, naive flow solutions (which should have TLE'd) ran in time. Thus, they simply kept raising the bounds until they got that solution to TLE. The judges, however, never considered that the data was just weak. They simply assumed there must be some special property in the graph which allows the flow to run fast. This sadly is not the case =(
G is a flow problem with V = nmlgnlgm + k, E = 4k + 2nmlgnlgm. Also, someone I know wrote E = O(klgnlgm) (approx 15M edges) and passed. In this problem, I think author needed big constraint to force his solution (although, surprisingly, this failed.)
I was also curious about the time complexity of flow algorithm. This is the "fact" I know about time complexity of flow algorithm :
Ford fulkerson is O(NM^2), Dinic is O(N^2M). (You can solve a problem about making Dinic TLE with O(N^2M) operation, on here)
Both are O(fE) of course
If it have unit edge capacity, Dinic runs in O(M^1.5). This was proposed in some CF round in last year.
This was what people usually say about time complexity of flow algorithm :
Ford fulkerson is fast, and Dinic is super fast
You need a lot of experience
If you can't solve with Dinic, that is not a flow problem
I'm not sure it is a good practice. If you are sure that is not a good practice, please update this article.
In case of unit capacity Dinic works in
I'm aware of proof for O(EV2 / 3) but I never heard of faster one. Can I ask about some resources for it?
I don't remember where I have seen it. Proof looks very likely to the proof of Hoproft-Carp maximal matching algorithm.
You can find it on e-maxx.ru
Would you spell it out a bit more?
The "special cases" section in https://en.wikipedia.org/wiki/Dinic%27s_algorithm gives that running time only for bipartite matching.
That runtime needs the additional requirement of in degree 1 or out degree 1 for each node. The bipartite matching case meets this requirement.
At first, I accidently gave one downvote to this reply. Does that explains it's -15 downvote?
Here 3053014 is the push preflow algorithm implementation that is faster than Dinic (for the given problem), so Dinic not always the fastest flow algorithm.
I was (and probably, they were) aware of push flow algo for maxflow. I just wanted to stress out that the problemsetter don't usually force it, even though there might be a case that I want to force my non-model flow sln to pass.
How to solve E?
Add X to the cost of each edge that connects a special vertex and a non-special vertex, and find an MST in this graph.
If you are lucky and this MST contains exactly k edges between special vertices and non-special vertices, this is the answer.
Otherwise you should change the value of X to be "lucky" — do binary search on X.
Why does there exist such X that the MST contains exactly k edges? We had this solution accepted, though we had to consider carefully the cases where we can add either special or non-special edge to the MST.
That is a truly amazing solution. Is there any other solution that ordinary people can think?
How can we prove that the k edges obtained in this process would correspond to the final answer?
Take complete graph, all edges have weight 1, k is somewhere in the middle.
More precisely, for a fixed X, I computed LX and RX — the minimum/maximum possible number of special edges in an MST. Then LX + 1 = RX.
I believe if x is double
Still not obvious how to restore the answer
Probably one can think in this way. Let the answer tree be T and its cost to be C. Suppose when you add weight x to each special edge, you can construct an MST T' with k special edges, and the cost of T' is C'.
(1) If we subtract weight x for each special edge of T', we still get a spanning tree with cost C'- k*x.By the property of our answer tree, C <= C'- k*x.
(2) If we add x for each special edge of T, we get a spanning tree with cost C + k*x. Then by the property of T', we have C' <= C + k*x.
(3) By (1) and (2), C = C'-k*x.
So if we can find such an x to we can construct an MST with k special edges, we can simply output C'-k*x, and no solution otherwise? (not sure)
It sufficient to consider only integer x because sorting of edges by weight changes only in integer points. To get Lx in case of equal weights we prefer usual edges, opposite for Rx. If x is increased by 1, then all special edges jump to next weight and order of edges in Rx and Lx + 1 will be the same.
To get spanning tree with Lx ≤ k ≤ Rx edges, we can consider intervals of edges with equal weights independently (because for prefix of edges we will always get the same set of components regardless of their order in Kruskal's algorithm). To get spanning tree with any possible number of special edges one can build components using only usual edges, then add all necessary special edges (there are Lx of them), then add any subset of spanning tree on remaining special edges.
black magic
http://codeforces.com/contest/125/status/E
I have been solving that problem maybe 4 years ago and already forgotten about it :(
How to solve D?
DP on subtrees with merging sets. First, make all numbers different. Let d(x) be the answer at some subtree if all taken vertices have value ≤ x. We store in a set all such x that d(x) ≠ d(x - 1) (note that in this case d(x) = d(x - 1) + 1).
Now if you look at the transition formulas (or stare at the values of these sets on some examples) you will see that the recalculation is similar to finding the LIS. First, we merge the sets of the children. Second, we replace the value set.upper_bound(wv) with the value wv or add it to the set if upper bound does not exist. The answer is the size of the set in the root.
Honestly, I don't know how to come up with this solution without staring at the examples.
For motivation, you can notice is if the tree is a line graph, then this is exactly computing LIS on the sequence. Anyways, here's a short implementation of the above approach:
Can you share some similar problems
How to solve A?
Sort all bracket sequences according to some weird combination of minimum depth and sum , then do DP.
We got this by just trying several sort functions. Is there intuition for why this one is correct?
You can mention some combination?
You can mention any?
pre = minimum prefix sum
len = length of bracket
sum = sum ( = +1 and ) = -1
Note that i am not sure why it worked , i tried several combinations until i got ac.
I tried to find a specific combination for around 2 hours in the contest, got super frustrated, wrote several comparators and ran the DP against them all, and printed the maximum answer (AC). Wasted almost entire contest on A :/
Similar idea to this world final problem. https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=715&page=show_problem&problem=5609
How to solve B?
Once you know the plane where one of the bases is, you can project all the points on it, and the result will be the maximum distance to that plane (height of the cylinder) * area of minimum circle that covers the projected points (a 2D problem for which there is a randomized algorithm with expected runtime O(N) ).
The problem is finding those planes, since it takes too long to check all the candidates, even with the information that there are at least 3 points on one of the bases. I've tried all sorts of tricks and randomized checkers and failed during the contest, and the only way I could get accepted afterwards was with 3d Convex Hull (the planes we are looking for will be the planes of the hull faces which I'm pretty sure are at most O(N)).
I'm really curious if others got it without Convex Hull.
You need to do 3d convex hull, then apply steps above. The 3d convex hull is made slightly easier by the fact that you can do it in O(n^2).
For instance, here's my code for 3d convex hull using gift wrapping (~10-15 lines).
That's a nice idea, but how do you find any edge from convex hull?
We used incremental approach to find convex hull, it's also fine (add vertices one by one and update faces).
You can project it to the xy plane and find an edge of the convex hull there. For example, ignore z coordinates and take the lowermost leftmost point, the crossing most clockwise point will give you an edge on the convex hull. Someone else also had an incremental hill solution that was pretty short. It also has the added advantage of handling four colplanar points more robustly.
sorry for necrobloging but why this solution will find all faces?
How to solve C?
It could be solved using dynamic programming.
Firstly, "There is exactly one path, going from streamer to streamer, between any two students in the circle." means that the resulting graph is a tree with n students as vertices and n-1 streamer as edges.
Secondly, "No streamers may cross." indicates that if there's a streamer connecting student i and student j, then after erasing this streamer, we are left with one tree of all student in range (i, j) and another tree of all students in range (j, i). Note that the interval here is cyclic. For example, n = 10, (8, 4) represents {9, 10, 1, 2, 3}, and (4, 8) represents {5, 6, 7}.
This gives us a way to define DP states. Let dp(int i, int j, bool connected) be the number of ways to construct a tree for students in range [i, j], and there's a direct streamer between i and j if connected is true while there's no direct streamer between i and j if connected is false.
The final answer is (dp(1, n, true) + dp(1, n, false)) % 1000000007.
Any hint on problem H?
It's hard to give a small hint, but you can look at the first sample a bit more closely
I added a big hint below:
Try to prove the following: There is no cycle with mentioned properties -> there is a "monochromatic" node (i.e. a node where all of its edges are the same color).
It's easier to prove contrapositive: Every node has two edges of different colors -> there is a cycle with mentioned properties
Thank you!
We need to prove that for any graph (all cycles are good) => (there is at least one monochromatic node).
For V = 3 it is true. Suppose it is true for all graph with less then V nodes. Consider graph with V nodes and node with maximum number of incident edges with equal color. Let's call this node 0. There is a monochromatic node in subgraph without 0 node, so number of equal edges is at least V - 2. If it is V - 1 then we are done. Suppose there are V - 2 edges with color 0 and one edge with color 1 going to node x. Then bad cycle must contain node 0, because all other are good by induction. Also x must be it's second node. So we are going 0 → x. x is not monochromatic so it must have at least one outgoing edge with color ≠ 0 (say, other end of this edge is y). If edge's color ≠ 0 and ≠ 1 then 0 → x → y → 0 is a bad cycle and we are done. So it's color is 0. By the same logic we find edge from y with color 1 going to some node z ≠ x. Then we get bad cycle 0 → x → y → z → 0.
Now we can enumerate all nodes in such a way that all edges (i, j)|i < j have the same color for fixed i. Let's associate this color with node i. Now clique is the subset of nodes with equal associated color plus possibly some node with greater number in our order. To get the answer we can fix the last node in set S from the statement, fix x + 1 as the size of maximal sub-clique and then calculate number of subsets with ≤ x nodes of equal color (for each color). And finally subtract answer for all smaller x.
Thank you!