Problemset was formed by Oleg snarknews Khristenko.
Problem A. Arithmetics Problem
In this problem your task was to implement exactly what is mentioned in this statement — iterate over all integers starting from 1 looking for the integer that is not a divisor of n and output it. Despite the fact n may be pretty large, this works really fast because in the constraints of the problem the answer is no more than 23 (least common multiplier of all integers between 1 and 23 is 5354228880 that is already bigger than n).
This was one of the simplest problem of the contest, but still, many contestants were hurrying too much and got WA 4 on the first minutes of the contest because they were iterating up to n, but not to infinity. Such a solution doesn't work for n = 1 and n = 2. What a pity it must be to make such a bug when submitting the problem blindly :)
Problem B. Building a Quadrilateral
As well as the problem A, this problem was pretty easy. You had to remember the criteria of a quadrilateral being circumscribed: quadrilateral is circumscribed if and only if sums of its opposite sides are equal. So, the correct solution looks like: consider all three possibilities to divide four input numbers into two pairs (ai, aj) and (ak, al) and check that ai + aj = ak + al. In particular, there is no need to manually check that these four segments may even be combined into any quadrilateral because this immediately follows from the equation above.
Problem C. Cyclops and Lenses
This is a greedy problem. Let's say that cyclops form a pair if they wear lenses from the same lense pair. Obviously, we want to maximize the number of cyclop pairs.
Consider a cyclop with smallest li, let this value be x. Obviously, it may be paired only with cyclop with either the same value of lj = x, with lj = x + 1, or with lj = x + 2. Let's present a sketch of a proof of the following fact. It is true that cyclop i should be paired with a cyclop with minimum lj among the remaining ones, lj - li ≤ 2.
Let's prove that if we have a cyclop with lj = x, then in some optimum answer cyclop i will form a pair with cyclop j.
If cyclop i is unpaired then simply form a pair of (i, j). This doesn't change the number of pairs or increases it by 1.
If i is already paired with some cyclop k (lk - li ≤ 2), and cyclop j is paired with cyclop t, it is always correct to repair them as follows: i with j and k with t.
You may similarly prove the general statement.
So, we got a simple greedy algorithm (much simpler than its strict proof!): we iterate over cyclops in an ascending order of their li and try to pair each cyclop with a following one if it is possible. In case of failure we buy a pair of lenses only for i-th cyclop and move to the next cyclop, otherwise we buy a pair of lenses for two of them and move forward. This solution works in time of sorting all the integers in the input.
Problem D. Two transformations
First of all, replace each number in the input with its remainder modulo 2. Consider the special case of n = 1 manually.
Note that we have n - 2 operations, such that all of them look like inverting three adjacent elements except the two special operations that look like inverting first two or last two elements.
Obviously, the order of operation applying doesn't matter, so, each operation should be applied no more than once. Suppose that we are trying to make all number even, i.e. zeroes. Consider two cases: either we use the operation of inverting first two elements or not. If we decided to use it, invert x1 and x2.
Now all operations are of the form "invert all numbers xi, xi + 1, xi + 2 (in case it exists)" over all i between 1 and n - 1. Note that it is now uniquely determined if we are going to use each next operation: indeed, if x1 = 1, then we will definitely use the first operation, otherwise we won't. Invert x1, x2, x3 if needed, then, by looking on x2 we uniquely determine if we need to use the second operation, and so on.
In such manner we will make all elements of the sequence except, possibly, last one, be equal to zero. If the last element is not zero, then the decision we made at the beginning (about using operation over x1 and x2) was wrong, and it is impossible to achieve the desired situation in it. Otherwise, since we performed uniquely on each step, we also know the minimum number of operations required for the case we fixed at the beginning.
Find the overall answer as the minimum of answers over those two cases.
Solve similarly for making all numbers odd. The complexity of a presented solution is O(n).
Problem E. Points and Circles
This problem allows two approaches. One is to implement exactly what is required in the statement, namely: you fix three white points i, j and k, check that they are not collinear, build their circumference and explicitly count all the points inside it. Such a solution runs in time of O(w3r) and should be implemented carefully (in particular, it's good idea to consider only triplets (i, j, k) such that i < j < k, reducing the solution space by factor of about 6). Also, it is a good knowledge how to effectively check the point for belonging to a circle that uses only integral arithmetics of 4-th order int respect to the magnitude of input coordinates. It may be shown that the point p = (px, py) lies inside the circumference of points a = (ax, ay), b = (bx, by), c = (cx, cy) if and only if the sign of determinant
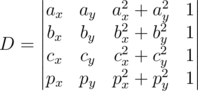
is same as the sign of determinant
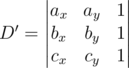
Such a solution requires only the integral calculations, it is absolutely precise and pretty efficient.
This problem also allows a solution in time of  using the geometric inversion transformation, but we will not discuss it since it's running time is about the same as the running time of a solution above.
using the geometric inversion transformation, but we will not discuss it since it's running time is about the same as the running time of a solution above.
Problem F. Cable management
This problem may be reduced to a minimum cost problem.
We will try to build a network, such that each path from source to sink corresponds to some possible scenario of a certain patchcord usage. Recall that each patchcord appears at some moment of time (requiring cn money from us), after that it periodically uses on some days i, breaks, and after that it must either be repaired by a company (in this case it moves to the day i + tf in cost of cf), or be repaired by Byteasar (in this case it moves to the day i + ts in cost of cs), or it may finally be thrown away up to the end of conference.
Let's interpret it in the following manner: consider the network that has the source s, the sink t, and also n pairs of vertices (1 + , 1 - ), (2 + , 2 - ), ... (n + , n - ) corresponding to each of the day of the conference. The idea behind assigning each day to two vertices will be clarified later.
Let there be an edge from source s to the vertex i - of cost cn and capacity ∞. Unit flow through this edge corresponds to a single bought patchcord.
Let there be an edge from vertex i + to the vertex i - of capacity ri and cost - A where A — is some positive amount. The unit flow through such an edge corresponds to a single patchcord used in day i. Let's call such edges important.
Hence, all patchcords getting to the vertices of kind i - are broken patchcords that require repairing.
Let there be an edge from vertex i - to the sink t of capacity ∞ and cost 0. Unit flow through this edge corresponds to throwing out one patchcord.
Let there be an edge from vertex i - to vertex (i + tf) + of capacity ∞ and cost cf. Unit flow through such an edge corresponds to repairing of one patchcord using the company.
Similarly, let there be an edge from vertex i - to the vertex (i + ts) + of capacity ∞ and cost cs. Unit flow through such an edge corresponds to one patchcord repaired by Byteasar.
Finally, let there be an edge from vertex i + to the vertex (i + 1) + of capacity ∞ and cost 0 Unit flow through such an edge corresponds to an unbroken patchcord that was not used during the day i.
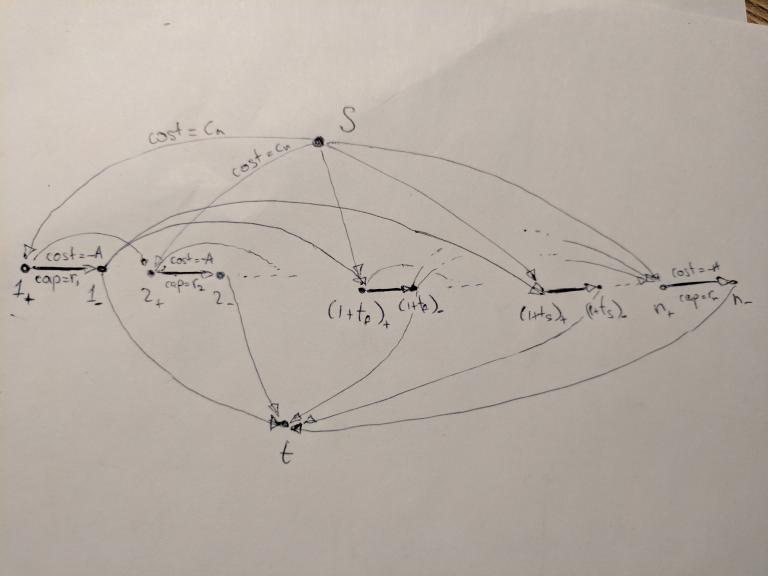
Any feasible flow in such a network corresponds to some set of patchcords and a strategy of their usage, but this set of patchcord may not be satisfying the requirements for the amount of patchcords per each day. We are interested only in those flows that saturate all the important edges.
Let's use a standard trick -- let's find the minimum cost flow, assigning all important edges a very small negative capacity beforehand. In the other words, let A be equal to a very large positive number. Then the final cost of a flow will be equal to - A·satcnt + opcost where satcnt is the number of saturated important edges, and opcost is a cost of buying/repairing all the broken patchcords.
Let's find the flow of minimum cost in this network (note that it is not the same as the maximum flow of minimum cost). It's easy to see that such a flow maximizes the number of saturated important edges, and in case of a tie it minimizes the total expenses in a chosen plan.
So, we have a solution that has the running time of running a min-cost-flow algorithm in a network without negative cycles. Algorithm of repeated finding the shortest augmenting path using Ford-Bellman's algorithm works without any issues in constraints of the problem.











ad E: Determinants are sorcery, inversion is dark sorcery. My solution in for non-wizards uses the fact that if
for non-wizards uses the fact that if 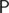 lies in the circumcirle of
lies in the circumcirle of  , then
, then 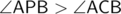 or
or 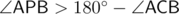 for
for  respectively on the same side and on opposite sides of
respectively on the same side and on opposite sides of  (collinearity is a special case). Angles can be computed using the law of cosines. If we fix
(collinearity is a special case). Angles can be computed using the law of cosines. If we fix 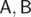 , the problem becomes sorting and two-pointer (well, 3-pointer if we split red points by
, the problem becomes sorting and two-pointer (well, 3-pointer if we split red points by  ) iteration. Precision wasn't an issue here thanks to additional constraints.
) iteration. Precision wasn't an issue here thanks to additional constraints.
I think problem E's D' is not correct. It doesn't pass first sample.
Is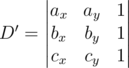 correct?
correct?
Yes, you are right. That is a typo, as it was already noticed in Russian version of the site. Fixed.
Geometric meaning of sign(D') in this formula is 2-d orientation of triple a, b, c.