Hey guys,
Convex hull optimization is a well known technique used for speeding up dynamic programming algorithms.A thorough explanation of the technique can be found in the end of the post at (1). You can also check the codeforces blog post about various dynamic programming optimizations at (2). I made this blog post to explain how to make convex hull optimization fully persistent. Even though the persistent version consists of a very natural extension of the original data structure I couldn't find anything with a quick search on google, therefore i decided to share it with the codeforces community. So here it goes.
At first let me state the problem. We want to construct a DS which can support the following operations:
- Insert a line in the DS, given by a pair (a,b) which represents the slope of the line and the vertical displacement. We demand that the line we are inserting has greater slope than any of the lines previously on the DS.
- Given a vertical line x = x0, find the line in the DS which intersects the vertical line higher than any of the other lines in the DS. Basically we are searching for the line y = ai * x + bi for which the system of equations
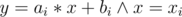 has a solution (x, y) for which y is maximum.
has a solution (x, y) for which y is maximum.
This is the original version of the convex hull problem. In order to get the fully persistent version of the problem we also demand that we can modify an older version of the DS and also query a certain version of the DS. To clarify, when we talk about versions of the DS we consider that version 0 consists of the empty data structure and every insertion defines a new version of the DS.
In order to support the operations above we will use a technique similar to that of a persistent stack. We will build a rooted tree so that every node represents a line and a node to root path represents a version of the stack. The root represents the empty stack. We maintain a pointer that points to the current version of the DS. To insert a line to the current version, we simply insert a child from the current version to a new node that contains the line to be inserted and we update the pointer. For example if we add the following lines: (1, 2), (2, 3), (3, 5) our DS will have the following form: 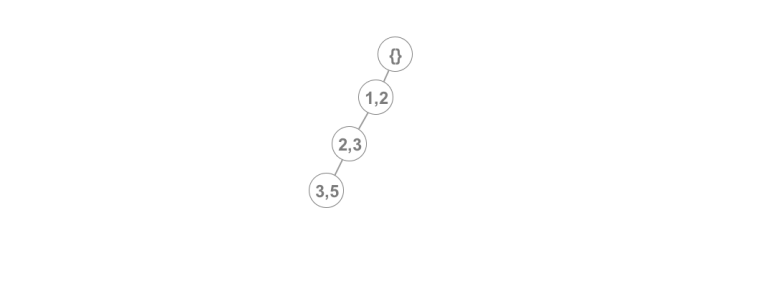
We use this model to support the persistent operations. When we want to add a line to a specific version we simply find the node that represents that version in our tree model and we add a new branch containing our line. To be able to do that we also need a version to node correspondence but this is easy to maintain with a simple array. Therefore if we wanted to add a line (e,g (4,5)) in version 2 of our DS we simply add a new child. Therefore we would have something like this:
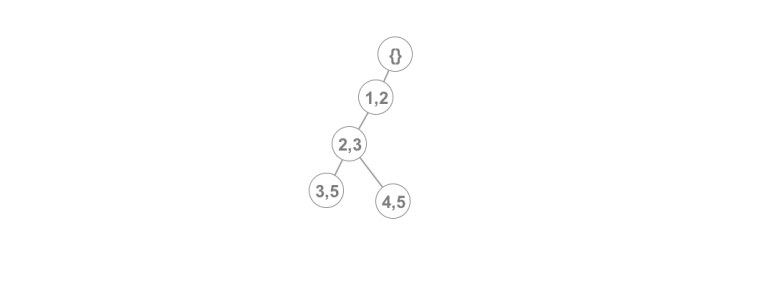
Of course, when we add a specific line to a version, some of the lines may become irrelevant (i.e Never be optimal). therefore, if that's the case, we pop from the top of the stack until our lines are relevant. Of course, popping in our current setting is equivalent to traversing from the node of the current line in that version of the DS to the root and updating the version settings. This may create a problem in the complexity of our structure since we cannot make the same amortization argument we do in our original version (We may be asked to traverse to the root multiple times). We will see how to resolve that shortly.
The question remains though, how could we query a version of our DS represented in the way we described above. We will use jump pointers. Every time we insert a line to a specific version we create links to its 2k - th parent for all k in the same way we do it for LCA. Now, in order to query a version we go to the node that represents the version in the tree and using the jump pointers we perform a binary search. Remember that we only care about the path from the specific node to the root since that's what our stack consists of in that version. Let's use u to represent our node in question (the version we are querying) and let P[u, k] be the 2k-th parent of node u. We find the largest k for which 2k ≤ depthu and we operate similarly to the original version of the problem. We check the node v = P[u, k] and its parent p(v), if the line that is stored in p(v) intersects the vertical line higher than the line stored in v we go to v and continue our search from there. Otherwise we decrease k and continue.
By using jump pointers we can also resolve the problems we had updating the data structure. We will simply perform a binary search to find the first line in the node to root path that should not be erased from the DS and add a child to that specific node. The binary search condition is the same as with the original version of the DS.
Therefore we have achieved to support our operations in O(NlogN) space O(logN) worst case time for update and query.
(2) Dynamic Programming Optimizations
I am sure that a similar idea is probably discussed somewhere, I just felt like sharing it since i think that it can be used for many cool problems. If you know any problems that can be solved using this technique please add them in the comments. Feel free to make any corrections or point out any mistakes, there might be quite a few of them.











CEOI 2009 — Harbingers http://ceoi2009.ro/tasks/harbingers.pdf
Note that simpler solution exists. Still it is solvable that way (I know someone who ACed with that method)
Idea is basically simillar, but this exploits the nice property of tree traversal, reducing lot of implementation details (such as level ancestor).
We need to maintain all DP values in the ancestors. When we move down one node, we insert a line which might reduce the # of active lines. But if we move up to parent, we should recover the stack which parent previously had! This is directly solved by using above persistent structure, but note that the stack don't encounter big changes : We just reduce it's size, and replace some value in array to another one!
So, to maintain parent's stack, we just store the previous size, and one information about array replacement while recursion. After recursion, we undo it. This can be interpreted as storing the list of "undo"s, in call stack.
For details conduct the official solution.
Very nice, thank you for sharing.
Although, as you mentioned, this problem can be solved in a relatively easier way since we are traversing the tree and we only care about specific paths. It seems like an offline version of the above technique.
I think the simpler solution is still O(n2).
It is true that the restore operation is O(1). But after restore the complexity of an add line operation doesn't remain O(n) amortized, it becomes O(n2) overall.
Consider a tree with n nodes. First there is a chain of length n / 2, and the last node has n / 2 childs. Now assume there is a particular line that removes all of O(n / 2) lines of the chain. Set this line to the n / 2 leaf nodes.
Now, in your approach, an add operation from the leafs will remove n / 2 lines, a restore will add all those lines again, in O(1) but that doesn't matter. Total complexity becomes O(n2) again.
It happens beacuse when we prove the amortized complexity O(n) for add lines, we assume that a lines gets added 1 time, and removed atmost 1 time. But that is not true after restore operation. How you're gonna deal with this?
Why so few upvotes? He has indeed dug a fishy thing from a red coder's comment!
To find an inserted position for a line, do binary search — Just like the author of this article did.
And what’s really “fishy” here? This detail is obvious if you read the article.
It doesn't remain simple then. Many people saw your comment and got misguided.
Aaaaaaaaah, that’s what I have to hear from you, when the writer of the article used one paragraph to talk about O(lgN) insertion, and I came here to help by giving some tips?
Actually I meant "Fishy in his way" :P
seems so legit
The link for the task seems to be broken. Can anyone link some tasks that require Persistent Convex Hull Trick?
This is a working link for CEOI 2009: Harbingers.
https://www.hackerrank.com/contests/w36/challenges/expert-computation/problem
It only works when slopes are increasing (in case for an upper convex hull) .Do you have a way to maintain dynamic convex hull (in persistence)??
you can use persistent treap with finding leftmost and rightmost lines that needs to be deleted, and then cut this segment with two split and one merge.
Can you mention some good links to learn about treap and persistent treap ??
Here's a good source for Treap:
1)Basics of Treap
2) Implicit Treap
Or you can use persistent dynamic LiChao segment tree, because it's just much easier to implement and also it's faster.
What's a LiChao segment tree?
Link.
Thank you! :)
I did not write it completely clear though but I can give you the implementation of it. http://ideone.com/qnoAgO Hope that helps. Cheers
You're welcome. Here is my implementation for just dynamic LiChao segment tree (assuming that the query points we need are integers) — link. It can be easily extended to become persistent.
You don't need to created two version for maximum and minimum.
You can query minimum value from a maximum LiChao tree by adding line (-a, -b) instead of (a, b), and getting -query(x) instead of query(x). This applies to convex hull too.
you mean for dynamic convvex hull on trees??
yes
I just tried the Harbingers problem, then read this post and I just wanted to share my code of the described data structure, hope someone finds it useful.