witua's blog

Codeforces Round #136 — Editorial
By witua, 10 years ago, In English

221A - Little Elephant and Function

In this problems you should notice that the answer for the problem is always of the following form: n, 1, 2, 3, ..., n-1. In such case array will be always sorted after the end of the algorithm.

221B - Little Elephant and Numbers

Here you just need to find all divisors of n. This can be done using standart algorithm with iterating from 1 to sqrt(n). After that you need to write some function that checks whether two numbers has same digits. This also can be done using simple loops.

220A - Little Elephant and Problem

There are multiple possible solutions for this problem. For example, the following. Find the last index x such that there exists some y (y < x) (minimal possible) that Ax < Ay. Then you just need to try two possibilities — either swap Ax and Ay, or don't change anything.

220B - Little Elephant and Array

This problem can be solve in simpler O(NsqrtN) solution, but I will describe O(NlogN) one.

We will solve this problem in offline. For each x (0 ≤ x < n) we should keep all the queries that end in x. Iterate that x from 0 to n - 1. Also we need to keep some array D such that for current x Dl + Dl + 1 + ... + Dx will be the answer for query [l;x]. To keep D correct, before the processing all queries that end in x, we need to update D. Let t be the current integer in A, i. e. Ax, and vector P be the list of indices of previous occurences of t (0-based numeration of vector). Then, if |P| ≥ t, you need to add 1 to DP[|P| - t], because this position is now the first (from right) that contains exactly t occurences of t. After that, if |P| > t, you need to subtract 2 from DP[|P| - t - 1], in order to close current interval and cancel previous. Finally, if |P| > t + 1, then you need additionally add 1 to DP[|P| - t - 2] to cancel previous close of the interval.

220C - Little Elephant and Shifts

Each of the shifts can be divided into two parts — the right (the one that starts from occurrence 1) and the left (the rest of the elements). If we could keep minimal distance for each part, the minimal of these numbers will be the answers for the corresponding shift. Lets solve the problems of the right part, the left will be almost the same.

Let we have some shift, for example 34567[12] and the permutation A is 4312765 and B is 2145673, then shifted B is 4567321. Let we keep two sets (S1 and S2). The first will keep all the distances from integers in current left part to the corresponding positions in A (for the example above, it is \texttt{2, 4}). When you come to the next shift, all integers in S1 should be decreased by 1 (that is because all distances are also decreased by 1). But now some integers in set may be negative, when any negative integer occures (it always will be -1) you need to delete it from S1 and put 1 to the S2. Also after shifting to the next shifts, all integers in S2 must be increase by 1. After that, for any shift, the answer will be minimum from the smallest numbers in S1 and S2.

It was very useful to use standart "set" in C++.

220D - Little Elephant and Triangle

Let iterate all possible points that, as we consider, must be the first point. Let it be (x;y). Let the second and the third points be (x1;y1) and (x2;y2). Then the doubled area is |(x1 - x)(y2 - y) - (x2 - x)(y1 - y)|. We need this number to be even and nonzero. For first we will find the number of groups of points that are even, after that just subtract the number of groups with area equal to zero.

For the first subproblem, we need to rewrite our formula. It is equal to |x(y1 - y2) + y(x2 - x1)|. Since we know x and y and we just need to check parity, we can try all possible 24 values of parity of x1, y1, x2 and y2 (let it be d0, d1, d2 and d3, respectively). And check whether they will form a 0 after multiplications and taking modulo 2. If it froms a 0, then add to the answer value cxd0cyd1cxd2cyd3, where cxd is equal to the number of integers between 0 and n, inclusve, that modulo 2 are equal d. cyd is the same but in range [0..m].

Now we need to subtract bad groups — the ones that has the area equal to zero. This means that they will either form a dot or a segment. If it is segment, we can just iterate dx = |x1 - x2| and dy = |y1 - y2| instead of all 4 coordinates. Then the number of such segments on the plane will be (n - dx + 1)(m - dy + 1). Also for counting the number of triples of points on the segment you need to find the number of integer coordinates on the segment. It is well-know problem, and the answer is gcd(dx, dy) + 1.

This gives us, with some simple optimizations, and O(nm) solution.

220E - Little Elephant and Inversions

In this problems you can use a method of two pointers. Also some RMQ are required. If you do not know about RMQ, please, read about it in the Internet before solving this problem.

Firstly, map all the elements in the input array. After that all of them will be in range [0..n - 1]. We need to keep two RMQs, both of size n. Let the first RMQ be Q1 and the second Q2. Q1i will contain the number of numbers i in current left subarray. Q2i will contain the number of numbers i in the left subarray. Firstly, add all n number to the Q2. After that iterate some pointer r from n - 1 downto 1, by the way keeping point l (which, at the beggining, is equal to n - 1) Using RMQs, you can keep the number of inversions when you decrease r or l (using "sum on the range" operation). While the current number of inversions is more then k and l ≥ 0, decrease l. Then for each r the answer of correct l will be l + 1 (considering 0-based numeration).

This makes the algorithm working in O(NlogN) time with correct realisation.

 
 
 
 
  • Vote: I like it
  • +50
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +7 Vote: I do not like it

I can't understand why doubled area is:|(x1 - x)(y2 - y) - (x2 - x)(y1 - y)|...can any one tell me why?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    cross product?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Thank you...I am just on thinking about the meaning of this formula in classical geometry...a silly question...

      → Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

In Div 1, Problem B, what is O(NsqrtN) solution?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    For each two queries [l1, r1] and [l2, r2] we can easily change the first query to the second in no more than |l1 - l2| + |r1 - r2| operates.(adding or deleting the leftmost and rightmost elements and counting the number of times that each number appears)

    Sort all the queries by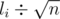 as primary sort key, and ri as secondary sort key. Now we can get a 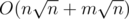offline solution.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why do you sort the queries by l/sqrt(n)

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Split l into groups. We can ensure that 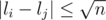if i, j are belong to the same group.

        So we can calculate the complexity as follow:

        1. = * m queries

        2. = O(n) * groups =

        → Reply
        • »
          »
          »
          »
          »
          7 hours ago, # ^ |
            Vote: I like it -8 Vote: I do not like it

          a very underrated explanation thanks dude i was struggling with this problem

          → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    There is a much easier one. Just considering number x that occurs at least x times in sequence a. It's not hard to prove that there are at most 2*sqrt(N) numbers to be considered.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can Anybody explain me , why are there at most 2*sqrt(N) of such numbers?. Thanks in advance.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        (C[x] means the times that x occurs in sequence a) if C[x]>=sqrt(N), the number of this kind x is no more than sqrt(N). otherwise the number of elements in sequence a is greater than sqrt(N)*sqrt(N)=N if C[x]<sqrt(N), 1<=x<=C[x]<sqrt(N)

        → Reply
    • »
      »
      »
      14 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      GREAT

      → Reply
»
10 years ago, # |
  Vote: I like it +14 Vote: I do not like it

220E — we use RSQ, not RMQ

→ Reply
»
10 years ago, # |
  Vote: I like it +4 Vote: I do not like it

220B: why has the proposed solution nlogn complexity? I mean, if for each x I need to sum up D_l, D_l+1 etc to answer to the queries (that in worst case start from 0 and end to x for each x), isn't it N^2?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    you can use segment tree to query 0 to x....

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      BIT is easier and faster to implement here.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In explanation of 220C, what does this mean " (for the example above, it is texttt{2, 4}) " ? Does it mean that left set has a minimum distance of 2 and right set a minimum of 4?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    \texttt was a tag, now it's fixed.

    [2, 4] is the set of distances in right part, i. e. distance from 1 in sifted B to 1 in A (it is equal to 4) and distance from 2 in shifted B to 1 in A (it is 2).

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Got it

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -8 Vote: I do not like it

In problem A, for example, n = 3, if the init array is (3, 1, 2) (author's solution), isn't the sorted array is (3, 1, 2) -> (3, 2, 1) -> (2, 3, 1)? Did I mis-understand something?

PS: I know it's weird for a purple to stuck at Div2-A, but this one confused me a lot...

Edit: I got it, the sort happened after we enter function f[x-1], so it should be (3, 1, 2) -> (1, 3, 2) -> (1, 2, 3). I don't know what happened with my brain today...

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

220B — Little Elephant and Array, can anybody explain me how the update (add 1 to D[|p| — t], add -2 to D[|p| — t — 1], and add 1 to D[|p| — t — 2]) work?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I had a different approach

    first of all count the numbers an remove numbers like x which occurred less than x times at all now you have at most O( sqrt(n) ) numbers.

    for each of these store the indexes. for example store the indexes in which x occurred in vector[x].

    now for each query(x,y) all you need to do is to binary search in each vector and find lower bound of x and upper bound of y( lets name them lbx and uby ) now we easily find out that x occurred ( uby-lbx ) times in [x...y]

    it will solve the problem in O( N*sqrt(n) + Q*sqrt(n)* log( vector size ) )

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      can u give some advice , i write by mo's algorithm but it gives me tle http://codeforces.com/contest/220/submission/17425102

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I think your algorithm runs in O(nsqrt(n)log(n) .It absolutely gets TLE. You can reduce log(n) to O(1) (remove or update operations) by just considering element which has value <= 1e5 . Cause every element greater than 1e5 can not contribute to the answer of a query . So you can use just a array instead of map

        → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        http://codeforces.com/contest/221/submission/27454046

        This is my AC solution using Mo's Algorithm just as described above upto 10^5 using array , map causes tle !!

        → Reply
        • »
          »
          »
          »
          »
          3 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          map gives TLE, but unordered_map will lead to AC.

          → Reply
        • »
          »
          »
          »
          »
          3 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Can you please explain to me this part of your code ?

          while(c_right <= right)
        {
            add(a[c_right]);
            c_right++;
        }
        while(c_right > right+1)
        {
            c_right--;
            remove(a[c_right]);
        }

          I don't quite understand how c_right act, like why it's while(c_right > right+1), and why left and right is not symmetric ?

          → Reply
          • »
            »
            »
            »
            »
            »
            2 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I suppose in this code, c_right is the right position "to be changed next", while c_left if the left position "that has already been changed". You can implement a version such that the left and right are symmetric. Remember to change the initial value of c_right if you wanna do so.

            → Reply
    • »
      »
      »
      2 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I have implemented the exact same logic but still getting a TLE.

      Can you please take a look at my code?

      72203897

      Thanks in advance.

      → Reply
      • »
        »
        »
        »
        2 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        Your code complexity is m*k*log(sz) where k = total numbers whose occurrence needs be checked(maximum = sqrt(n)) and sz = size of total occurrence of that particular number in array(it can be sqrt(n) don't know the maximum bound). log(sz) which adds larger constant is responsible for TLE.

        → Reply
    • »
      »
      »
      3 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      thank you for sharing your approach

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

220B — Little Elephant and Array this question can be solved by MO's Algorithm

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I was trying to solve 221B using query square root decomposition.

I tried the following solution which was getting TLE, while this similar solution passed.

The only difference between the 2 solutions is the extra use of containsKey in the TLE solution. From my understanding containsKey has constant time complexity, so it shouldn't really be decisive for the acceptance or not of the solution. Am I missing something here?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In case if anyone finds the explanation for Div2D/Div1B confusing, just Google "MO's algorithm". Can't believe this magic man...

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Little Elephant and Array can be solved with hashing. Since n*(n+1)/2<=100000, therefore n<=450, which is the condition for tightest constraints i.e. n=10000 and all numbers 'a[i]' are distinct and appear 'a[i]' times.

Solution: http://codeforces.com/contest/220/submission/20777330

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how for for problem D complexity can be achieved O(mn)

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Witua is known to set beautiful problems and this contest was fantastic !

Here are my solutions to the Div 2 problems of this contest.

In Div 2, problem D captured my imagination. So, I wrote an editorial about it here that explains both the approaches.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    I love your editorial. its very comprehensive

    → Reply
»
4 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Can anyone tell me why this code wrong : http://codeforces.com/contest/220/submission/41300881

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Shouldn't sqrt root decomposition work for 220B? Where am i going wrong? https://codeforces.com/contest/220/submission/41652936 Thanks in advance!

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

could someone explain 220C. Little Elephant and Shifts bit more

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve Div 1 B using sqrt decomposition rather than MO's algorithm??

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

My solution for div1C is a little different. I know this is an old problem but I found it really interesting.

Let's graph the problem. Let's assume each cyclic shift happens in 1 second. Plot time along the x axis and the absolute difference in positions in both arrays for each value along the y axis.

Observe that there can be only two possible values of the slopes of the lines in the entire graph — +1 and -1. The line for a particular value will have slope equal to +1 if the position of the value in that instant's cyclically shifted array b is <= its fixed position in array, otherwise its slope will be -1.

Moreover it's easy to notice that for a particular value, its slope value changes a maximum of 2 times in its graph.

So we can maintain two range minimum segment trees with lazy propagation range updates for slope value = +1 and -1, each of which store the minimum y-intercept value at each integer instant from x = 0 to n-1. Then for at any given x, the answer is $$$ min \ ( i \ + \ minimum \ y-intercept \ of \ slope \ = \ +1 \ at \ x \ \ = \ i \ ,-i \ + \ minimum \ y-intercept \ of \ slope \ = \ -1 \ at \ x \ = \ i \ ) $$$

Total complexity is O(nlogn)

My submission: 57004696

(I've shifted the entire graph by 1 unit to the right to avoid using a segment tree with 0-indexing in my submission)

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

"Q1i will contain the number of numbers i in current left subarray. Q2i will contain the number of numbers i in the left subarray." ?

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For those of you getting TLE in Square root decomposition try using a different comparator or try changing the Maps to array

You can check my submissions 80679872

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I dont get it to implement the tutorials solution to 220B - Маленький Слоник и массив

Can somebody link a submission implementing it? I did not found one because there are so much sqrt solution or something else.

→ Reply
  • »
    »
    2 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Hopefully this one is clear enough...

    And just look for MO's algorithm using square root decomposition i just learnt it yesterday actually..

    The main idea in sorting the query and taking most possible advantage of overlapping queries since we can do it offline.

    I also found this comment useful.

    → Reply
  • »
    »
    2 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Kinda late, but here you go, hope this helps.

    90807410

    → Reply
    • »
      »
      »
      2 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Please explain the 3 major update operations in your solution too it is not clear to me from tutorial and also from the submission.

      → Reply
»
6 weeks ago, # |
  Vote: I like it 0 Vote: I do not like it

learn a lot after solving Little Elephant and Inversions using binary indexed tree and cool idea of two pointers and inclusion exclusion principle

→ Reply
»
4 days ago, # |
  Vote: I like it 0 Vote: I do not like it

I solved it in a rather ridiculous manner. I created a segment tree to store the merge sort results at each recursion level. Then first I calculated the number of inversions at each index, from 0 to that index in one array, from that index to n — 1 in another array. Lastly, I used two pointers method to find the total number of inversions. If the total inversions in the array originally was greater than k, and the array had at least three elements, forward pointer pointed at 0, backward pointer pointed at 3, at each iteration, if the sum of inversions count of forward array (0 to forward pointer), backward array (backward pointer to n), and the number of inversions for each element in forward array to backward array (stored in variable named ptionk) was added to check if inversion count is greater than k, if so, backward pointer was incremented, else forward pointer was incremented. Each incrementation, I added the number of inversions increased or decreased (due to removing an element from backward array or adding an element to forward array) to ptionk. Am I the only one who did it like this

→ Reply