problem link- http://www.spoj.com/problems/BADXOR/
i am not able to think of any solution other then brute force ,can anyone explain me how to proceed or can anyone give hint to the problem .also any suggestion on such type of problem or some links of similiar based problem will also be helpful










Why is this downvoted? What's wrong with someone asking a problem? I hate it when someone needs help and the blog gets downvoted for no apparent reason -_-
Bob_and_Vagene The problem can be solved using dynamic programming. Let dp[i][j] represent the number of subsets formed from the first i elements that have a bitwise xor exactly equal to j. For calculating dp[i][j], either you pick ith element in your subset, or you don't, so dp[i][j] = dp[i-1][j] + dp[i-1][j^arr[i]]. Your answer will be summation of all dp[n][j] such that j!=b.
I attempted this solution using your method. It is giving Wrong Answer. Please Help!
There is one more solution.
Lets consider all numbers a[i] as bitwise vectors under . Let A be the set of vectors which we obtain if we applied Gaussian elimination proccess to a[]. Now we have some value b and we asked how many subsets of a[] have xor-sum equals b. If b lineary independent with vectors from A that we have no subsets from A which xor-sum equals b and indeed it means that no subsets from a[] have such sum. If b can be represented as a sum of vectors from A the answer is at least 1. Note that exist only one representation
. Let A be the set of vectors which we obtain if we applied Gaussian elimination proccess to a[]. Now we have some value b and we asked how many subsets of a[] have xor-sum equals b. If b lineary independent with vectors from A that we have no subsets from A which xor-sum equals b and indeed it means that no subsets from a[] have such sum. If b can be represented as a sum of vectors from A the answer is at least 1. Note that exist only one representation 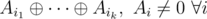 since for every bit no more than one vector can have 1 in this bit (because of G. Elim.). And thus all we can is add to our representation some subset of vectors from A which has zero xor-sum. All this vectors became 0 while we do GE. Denote their amount through K. Resulting answer equals 2N - 2K, where N is the number of elements in a[].
since for every bit no more than one vector can have 1 in this bit (because of G. Elim.). And thus all we can is add to our representation some subset of vectors from A which has zero xor-sum. All this vectors became 0 while we do GE. Denote their amount through K. Resulting answer equals 2N - 2K, where N is the number of elements in a[].