Div2 A. Parallelepiped
You were given areas of three faces of a rectangular parallelepiped. Your task was to find the sum of lengths of it's sides.
Let a, b and c be the lengths of the sides that have one common vertex. Then the numbers we are given are s1 = ab, s2 = bc и s3 = ca. It is easy to find the lengths in terms of faces areas: 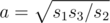 ,
, 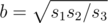 ,
, 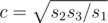 . The answer is 4(a + b + c), because there are four sides that have lengths equal to a, b and c. The complexity is O(1).
. The answer is 4(a + b + c), because there are four sides that have lengths equal to a, b and c. The complexity is O(1).
Div2 B. Array
You were given an array a consisting of n integers. Its elements ai were positive and not greater than 105 for each 1 ≤ i ≤ n. Also you were given positive integer k. You had to find minimal by inclusion segment [l, r] such that there were exactly k different numbers among al, ..., ar. The definition of the "minimal by inclusion" you can read in the statement.
Let us make a new array cnt. In the beginning its element cnti is equal to number of occurencies of number i in array a. It is possible to make this array because elements of a are not very large. Amount of nonzero elements in cnt is equal to amount of different elements in a. There is no solution if this number is less then k.
If it is not true, we have to find the answer segment [l, r]. In the beginning let [l, r] = [1, n]. We decrease its right end r by 1 until amount of different elements on the segment [l, r] is less than k. We can keep the amount of different numbers in following way: we decrease cntar by 1 if we delete element number r. Then we have to decrease current number of different elements by 1 if cntar becomes zero. After this we return the last deleted element back to the segment in order to make amount of different elements equal to k. Then we have to do the same with the left end l, but we have not to decrease but to increase its value by 1 on each step. Finally, we get a segment [l, r]. The amount of different numbers on it is equal to k and on every its subsegment is less than k. Therefore, this segment is an answer. The complexity is O(n).
Div2 C/Div1 A. Bracket sequence
You were given a bracket sequence s consisting of brackets of two kinds. You were to find regular bracket sequence that was a substring of s and contains as many << >> braces as possible.
>> braces as possible.
We will try to determine corresponding closing bracket for every opening one. Formally, let a bracket on the i-th position be opening, then the closing bracket on the position j is corresponding to it if and only if a substring si... sj is the shortest regular bracket sequence that begins from the i-th position. In common case there can be brackets with no corresponding ones.
We scan the sting s and put positions with the opening brackets into a stack. Let us proceed the i-th position. If si is an opening bracket we simply put i on the top of the stack. Otherwise, we have to clean the stack if the stack is empty or the bracket on the top does not correspond to the current one. But if the bracket on the top is ok we just remove the top of the stack and remember that the bracket on position i is corresponding to the bracket removed from the top. So, we find all the correspondings for all the brackets.
Then we can split s into blocks. Let block be a segment [l, r] such that the bracket on the r-th position is corresponding for the bracket on the i-th and there is no couple of corresponding brackets on positions x and y such that 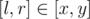 and [l, r] ≠ [x, y]. It is easy to understand that the blocks do not intersect and the split is unique. We can join the consequent blocks into the regular bracket sequences. We should join as many blocks as possible in order to get the maximal number of braces. We get several substrings that are regular bracket sequences after we join all the consecutive blocks. The answer is the substring that has the largest amount of braces <<
and [l, r] ≠ [x, y]. It is easy to understand that the blocks do not intersect and the split is unique. We can join the consequent blocks into the regular bracket sequences. We should join as many blocks as possible in order to get the maximal number of braces. We get several substrings that are regular bracket sequences after we join all the consecutive blocks. The answer is the substring that has the largest amount of braces << >>. The complexity is O(|s|).
>>. The complexity is O(|s|).
Div2 D/Div1 B. Two strings.
You were given two strings: s and t. You were required to examine all occurrences of the string t in the string s as subsequence and to find out if it is true that for each position of the s string there are such occurrence, that includes this position.
For each position i of the s string we calculate two values li and ri where li is the maximal possible number that the string t1... tli occurs as subsequence in the string s1... si, ri is the maximal possible number that the string t|t| - ri + 1... t|t| occurs in the string si... s|s| as subsequence. Let us find all of l for the position 1... i - 1 and want to find li. If the symbol tli - 1 + 1 exists and concurs with the symbol si then li = li - 1 + 1, in other case li = li - 1. In the same way we can find ri if we move from the end of the string.
Now we should check if the position i in the string s belongs to at least one occurrence. Let us assume this to be correct and the symbol si corresponds to the symbol tj of the string t. Then li - 1 ≥ j - 1 and ri + 1 ≥ |t| - j by definition of the l and r. Then if j exists that si = tj and li - 1 + 1 ≥ j ≥ |t| - ri + 1, then the position i of the string s belongs to at least one occurrence of the t, in other case the occurrence doesn’t exist. We can easily check it by creating an array cnta, i for each letter, which is a number of letters a in the positions 1... i of the string t. The complexity of the solution is O(|s| + |t|).
Div2 E/Div1 C. Частичные суммы
You were given an array a in this problem. You could replace a by the array of its partial sums by one step. You had to find the array after k such steps. All the calculations were modulo P = 109 + 7.
Write partial sums in following way:
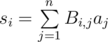
where Bi, j = 1 if i ≥ j and Bi, j = 0 if i < j, for each 1 ≤ i, j ≤ n. We can represent a and s as vector-columns, therefore one step corresponds to multiplying matrix B and vector-column a. Then the array a after k steps is equal to Bka. We can raise a matrix to a power for 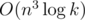 . It is not bad, but not fast enough.
. It is not bad, but not fast enough.
We can notice, that 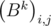 =
= 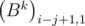 , i.e. the elements of the matrix Bk on diagonals parallel to the main are the equal. It is easy to prove this fact using mathematical induction. You may prove it by yourself. Then we can determine the matrix by an array of numbers
, i.e. the elements of the matrix Bk on diagonals parallel to the main are the equal. It is easy to prove this fact using mathematical induction. You may prove it by yourself. Then we can determine the matrix by an array of numbers 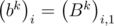 , equal to the elements of the first column. The elements of the first column of the product BkBl are equal
, equal to the elements of the first column. The elements of the first column of the product BkBl are equal 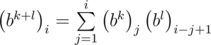 . It is a straight consequence of formula of matrix product. The computing of one element requires O(n) time, there are n elements therefore we can multiply matriсеs in O(n2) time. Then we can solve the problem in
. It is a straight consequence of formula of matrix product. The computing of one element requires O(n) time, there are n elements therefore we can multiply matriсеs in O(n2) time. Then we can solve the problem in 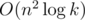 time and this solution fits the consrtaints.
time and this solution fits the consrtaints.
This problem can be solved faster. We can assure that 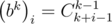 . Let this formula be correct for some k. Prove that it is correct for k + 1 either. Using the formula of product we get:
. Let this formula be correct for some k. Prove that it is correct for k + 1 either. Using the formula of product we get:
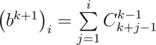
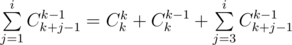
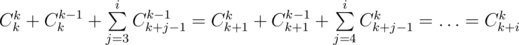
Используя формулу Cnk = n! / k!(n - k)!, можно получить, что 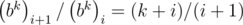 , поэтому мы можем построить все коэффициенты b, если умеем делить по модулю P, поэтому в этом решении существенна простота P. Обратный для числа x по простому модулю равен
, поэтому мы можем построить все коэффициенты b, если умеем делить по модулю P, поэтому в этом решении существенна простота P. Обратный для числа x по простому модулю равен 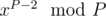 в силу малой теоремы Ферма. Таким образом, мы получаем решение за O(n2).
в силу малой теоремы Ферма. Таким образом, мы получаем решение за O(n2).
Using the formula Cnk = n! / k!(n - k)! we can obtain 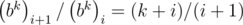 , so we can find all the coefficients b if we can divide modulo P. Therefore it is significant that P is prime. Inverse x modulo P is equal to
, so we can find all the coefficients b if we can divide modulo P. Therefore it is significant that P is prime. Inverse x modulo P is equal to 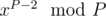 according to the Fermat little theorem. Therefore we get O(n2)solution.
according to the Fermat little theorem. Therefore we get O(n2)solution.
Div1 D. Spider
You were given a polygon consisting of n vertices, you had to find the shortest way from one of its vertices to another. You were allowed to move along the border and go stricktly down without going outside the polygon
All the sides of the polygon can be divided into three groups: top, bottom and vertical. The side is vertical if and only if the x coordinates of its ends are equal. The side is bottom if and only if the polygon's interior is above the side. The side it top if and only if the polygon's interior is below the side. We can descend only from points of the top sides to the points of the bottom sides. Vertical sides can be ignored because every descend that has common points with a vertical side can be splitted into two descends and one transfer. One can prove that it is useless to descend from a side's interior to side's interior. Len one of the descends in the optimal solution start in the inner point and end in the inner point. We can slightly change the x coordinate of the descend. The path's lenght is monotonically (possibly not strictly) depends on x, so we can move x in order to improve the answer. In case of not strictly monotone dependance the answer do not depend on x, so we also can move it. This proof is wrong if the descend passes through a vertex, therefore we have to examine all possible descends from the vertices and to the vertices.
We can solve this problem using scan-line method. We well move a vertical straight line from the left to the right and keep set S of the sides that intersect the line. We store the segments in the S in the sorted by y order. Let X be an abscissa of the line. The events happen during the moving: some segments are added to the S set, some are deleted. We can make an array of events, each events is described by its x coordinate that is equal to X of the line when the corresponding event happens, the number of the segment and a kind of event: adding or deleting. There are two events for every side, their x coordinates correspond to abscissas of their ends. The vertical sides can be ignored.
Let us proceed the events in non-decreasing order of x coords. If the current event is adding we add the side to S set. Then we check on its closest neighbours in the set. If the current segment is a top segment we can make a descend from its left vertex down to the intersection with it's lower neighbor. We find the point of the intersection, remember the segment where the point is located and remember that there can be a descend from a vertex to the new point. If the current side is the bottom side we make a descand from the upper neighbour to the left end of the current segment and do the same things. If the current event is deleting we analize its neighbours in the same way, but the descends start or end on the right end of the segment we are going to delete. It is important that if there are many events of one kind we should proceed them simultaneously, i.e. if there are many addings in the same x coordinate we must add all the segments and then examine their neighbours. It is the same for deletings: firstly we analize the neighbours for all the segments and only then we delete them. Also in the case of equal x coords of the events the adding events must be first, otherwise the solution is wrong for the case of two angles separated by a vertical line with vertices lying on this line.
Set S is easy to keep in container such as "set". We have to write a comparator for segments. We can do it in following way: two segments can be in S simultaneously if and only if there is a vertical line that intersects both of them. In common case such a line is not the unique, all the possible values of X are in segment [l, r] that can be easily found if we know the coors of the ends of the segments. Then we can choose an arbitrary X inside of [l, r] and compare the ordinates of the intersection points. Is better to choose inner point because in this case we don't have to examine special cases of segments having a common point.
After this we can build a graph. It's vertices are the vertices of the polygon and the ends of possible descends. The edges of the graphs are the sides of the polygon and the descends. The shortest path can be found using Dijkstra algorithm. The complexity of the solution is  .
.
Div1 E. Planar graph
In the problem we were given an undirected planar graph without bridges, cutpoints, loops and multiedge laid on the plane. We get requests of the following type: to calculate the number of vertices inside the cycle or on it.
Let us take an arbitrary vertex on the border of the graph, for example a vertex that has the least absciss. Let's add a new vertex with an edge to the chosen vertex in such way that the edge is outside the outer border of the graph. We'll call this new vertex a sink. Let's create a 1 value flow running to the sink from each vertex except the sink. Flow can be created using breadth-first or depth-first search. This operation will take the O(E) time.
Let's examine any request. We assume that the cycle is oriented counter-clockwise (if it is not so, we can just reorient it). Let's make a cut on the graph. The first part will contain the vertices laying on the cycle or inside it, the second one — all remaining vertices including the sink. We'll now prove that the flow value through the cut is equal to the vertices number in the first part. It's obvious that we can calculate contribution from every vertex to the flow value independently. Let's assume that the vertex is situated in the first part. A unit flow runs from it to the sink along some path. As soon as this vertex and the sink are situated in different parts the flow passes the edges of the cut an odd number of times, that's why the contribution of this vertex to the flow through the cut is equal to 1. Let's take now a vertex situated in the second part. As soon as it's situated in the same part as the sink the flow passes the edges of the cut an even number of times, that's why the contribution of this vertex to the flow through the cut is zero. In order to calculate the flow value through the cut we need to sum up flow values passing through the cut's edges. It's important to notice that every edge of the cut is incident to only one vertex lying on the cycle, that's why we can sum up flows passing though edges going outside the cycle for each vertex in the cycle. In order to find all edges going outside the cycle we'll sort all edges going from each vertex counter-clockwise by angle. In this case all edges going outside the cycle will be placed after the previous vertex of the cycle and before the following vertex of the cycle. That's why the sum of flow values over the edges going outside reduces to a sum over an segment which is easily calculated using partial sums. The complexity of the solution is 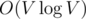 for graph sorting plus
for graph sorting plus 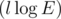 for the request where l is the cycle length. There is
for the request where l is the cycle length. There is 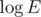 in complexity because we have to know a position of a vertex in the adjacency list of another vertex.
in complexity because we have to know a position of a vertex in the adjacency list of another vertex.











shouldn't the summation goes to n instead of i?
and if not, may some one explains to me why it is correct?
You're wrong because all the elements of Bk above the main diagonal are zero.
In Div2 Problem D, if I finished calculating the L[i] and R[i], how to check if a position 'i' is possible?
if L[i] >= R[i], then the i-th position is possible.
http://codeforces.com/contest/223/submission/2208834 But why this solution wrong?
I'm sorry that I misunderstood the meaning of L[i] and R[i]! I use L[i] and R[i] to represent the right most positon and the left most position that ith position can match. You can see my solution here. http://codeforces.com/contest/223/submission/2202460
Thanks for you help!
And can you tell me the main idea of your solution? How to calculate the left most position and right most position? I'm a little confused..
For L[i]: I use a array pos[26] to represent the right most position 26 letters can match.
for s[i], if s[i] can match t[j], s[i] = j; else s[i] = pos[s[i] — 'a'] j is the right most position that the string t1… tj occurs as subsequence in the string s1… si now.
Great solution to problem E.It is a good problem and I like it very much.
Agree! I never thought that it is related to flow. Very inspiring.
How could it be ??
Ck+1,k-1 = Ck,k ??
In problem Div2 A (Parallelepiped): According to tutorial 4*(a+b+c) is the answer. But, how can it possible when the output for the second test case (4 6 6) is 28?
Can anyone please explain? Only this formula ( 4*(a+b+c) ) is not working. I implemented it.
we have been given s1, s2, and s3 not a, b and c. According to the editorial, first find a, b, and c and then apply the same formula
4 * (a + b + c)