Hi. I already solved this problem by noticing that the sequence x1, x2, x4, x8, ..., x2n modulo 2010 is periodic with period 10 and pre-period 2. This means that 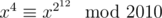 .
.
I would like to know a proof for this. Could you help me? You can find the problem statement here. It's the problem E.
Thanks beforehand.











The prime descomposition is 2010 = 2 * 3 * 5 * 67, so by Fermat's little theorem and the chinese remainder theorem any (inversible) element x modulo 2010 (not a mutiple of 2, 3, 5 or 67) will satisfy x132 = xmcm(2 - 1, 3 - 1, 5 - 1, 67 - 1) = 1. It just so happens that 212 = 4 + 132 * 31 which means that x212 = x132 * 31x4 = x4.
What about the non inversible elements? A weaker version of the previous will still hold and prove the periodicity. Write an element x as (x1, x2, x3, x4) in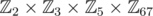 . The inversibility case from before is when each xi ≠ 0. If some of the xi are 0, then the others will still satisfy that xi132 = 1 by Fermat's little theorem. For example, we have (0, 2, 0, 23)132 = (0, 1, 0, 1). So, while x132 will not be 1 for these elements, it will still satisfy x132 * 31x4 = x4 because the zeroes are multiplying only zeroes and the other values are being multiplied by 1 s.
. The inversibility case from before is when each xi ≠ 0. If some of the xi are 0, then the others will still satisfy that xi132 = 1 by Fermat's little theorem. For example, we have (0, 2, 0, 23)132 = (0, 1, 0, 1). So, while x132 will not be 1 for these elements, it will still satisfy x132 * 31x4 = x4 because the zeroes are multiplying only zeroes and the other values are being multiplied by 1 s.