One can see that in the final set all the elements less than x should exist, x shouldn't exist and any element greater than x doesn't matter, so we will count the number of elements less than x that don't exist in the initial set and add this to the answer, If x exists we'll add 1 to the answer because x should be removed .
Time complexity : O(n + x) .
Solution link (me) : https://pastebin.com/ALfcu8Ab .
Solution link (mahmoudbadawy) : https://pastebin.com/yXLkmA5F .
862B - Махмуд, Ехаб и двудольность
The tree itself is bipartite so we can run a dfs to partition the tree into the 2 sets (called bicoloring), We can't add an edge between any 2 nodes in the same set and we can add an edge between every 2 nodes in different sets, so let the number of nodes in the left set be l and the number of nodes in the right set be r, The maximum number of edges that can exist is l * r, but n - 1 edges already exist so the maximum number of edges to be added is l * r - (n - 1).
Time complexity : O(n) .
Solution link (me) : https://pastebin.com/w3bF7gKS .
Solution link (mahmoudbadawy) : https://pastebin.com/PMpte7nC .
n = 2, x = 0 is the only case with answer "NO" .
Let pw = 217 .
First print 1, 2, ..., n - 3 (The first n - 3 positive integers), Let their bitwise-xor sum be y, If x = y You can add pw, pw * 2 and 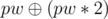 , Otherwise you can add 0, pw and
, Otherwise you can add 0, pw and 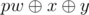 , We handled the case x = y in a different way because if we add 0, pw and
, We handled the case x = y in a different way because if we add 0, pw and 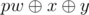 in this case, Then it's like adding 0, pw and pw, pw appears twice so we'll get wrong answer.
in this case, Then it's like adding 0, pw and pw, pw appears twice so we'll get wrong answer.
Handle n = 1 (print x) and n = 2 (print 0 and x) .
Solution link (mahmoudbadawy) : https://pastebin.com/w67KUY5u .
862D - Махмуд, Ехаб и бинарная строка
In the editorial we suppose that the answer of some query is the number of correct guessed positions which is equal to n minus hamming distance, The solutions in this editorial consider the answer of a query as n minus real answer, For convenience.
Common things : Let zero(l, r) be a function that returns the number of zeros in the interval [l;r] minus the number of ones in it, We can find it in one query after a preprocessing query, The preprocessing query is 1111..., Let its answer be stored in all, If we made a query with a string full of ones except for the interval [l;r] which will be full of zeros, If this query's answer is cur, zero(l, r) = cur - all, That's because all is the number of ones in the interval [l;r] plus some trash and cur is the number of zeros in the interval plus the same trash .
First solution by mahmoudbadawy
Let's have a searching interval, initially this interval is [1;n] (The whole string), Let's repeat this until we reach our goal, Let mid = (l + r) / 2 Let's query to get zero(l, mid), If it's equal to r - l + 1, This interval is full of zeros so we can print any index in it as the index with value 0 and continue searching for an index with the value 1 in the interval [mid + 1;r], But if its value is equal to l - r - 1, This interval is full of ones so we can print any index in it as the index with value 1 and continue searching for a 0 in the interval [mid + 1;r], Otherwise the interval contains both values so we can continue searching for both in the interval [l;mid], Every time the searching interval length must be divided by 2 in any case so we perform O(log(n)) queries .
Second solution by me
Let's send 1111... and let the answer be ans1, Let's send 0111... and let the answer be ans0, We now know the value in the first index (1 if ans1 > ans0, 0 otherwise), We can binary search for the first index where the non-found value exists, which is to binary search on the first value x where zero(2, x) * sign(non - found bit value) ≠ x - 1 where sign(y) is 1 if y = 0, - 1 otherwise .
Solution link (me) : https://pastebin.com/Bc6q7TKv .
Solution link (mahmoudbadawy) : https://pastebin.com/RMyLDMxw .
Let's write f(j) in another way:-
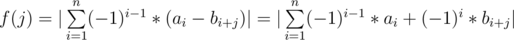

Now we have 2 sums, The first one is constant (doesn't depend on j), For the second sum we can calculate all its possible values using sliding window technique, Now we want a data-structure that takes the value of the first sum and chooses the best second sum from all the choices .
observation: We don't have to try all the possible values of f(j) to minimize the expression, If the first sum is c, We can try only the least value greater than - c and the greatest value less than - c ( - c not c because we are minimizing c + second not c - second) because the absolute value means the distance between the two values on the number line, Any other value will be further than at least one of the chosen values, To do this we can keep all the values of f(j) sorted and try the elements numbered lower_bound(-c) and lower_bound(-c)-1 and choose the better (In short we're trying the values close to - c only).
Now we have a data-structure that can get us the minimum value of the expression once given the value of the first sum in O(log(n)), Now we want to keep track of the value of the first sum .
Let the initial value be c, In each update, If the length of the updated interval is even, The sum won't change because x will be added as many times as it's subtracted, Otherwise x will be added to c or subtracted from c depending of the parity of l (the left-bound of the interval) .
Time complexity : O(n + (m + q)log(m)) .
Solution link (me) : https://pastebin.com/u828DjcS .
Solution link (mahmoudbadawy) : https://pastebin.com/dA3K8nfK .
862F - Махмуд, Ехаб и последнее испытание
First, Let's get rid of the LCP part .
observation: 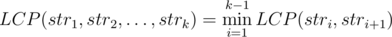 , That could make us transform the LCP part into a minimization part by making an array lcp where lcpi = LCP(si, si + 1), You could calculate it naively, And when an update happens at index a, You should update lcpa (If exists) and lcpa - 1 (If exists) naively .
, That could make us transform the LCP part into a minimization part by making an array lcp where lcpi = LCP(si, si + 1), You could calculate it naively, And when an update happens at index a, You should update lcpa (If exists) and lcpa - 1 (If exists) naively .
Now the problem reduces to finding a ≤ l ≤ r ≤ b that maximizes the value:-
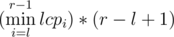 , If we have a histogram where the ith column has height lcpi, The the size of the largest rectangle that fits in the columns from l to r - 1 is
, If we have a histogram where the ith column has height lcpi, The the size of the largest rectangle that fits in the columns from l to r - 1 is 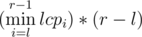 , That's close to our formula not the same but it's not a problem (You'll see how to fix it later), so to get rid of finding the l and r part, We can make that histogram and the answer for a query will be the largest rectangle in the subhistogram that contains the columns from a to b - 1, One of the ways to solve it is to try some heights h and see the maximum width we can achieve if h was the height, call it w, and maximize with h * w, To solve the slight difference in formulas problem we'll just maximize with h * (w + 1)!!
, That's close to our formula not the same but it's not a problem (You'll see how to fix it later), so to get rid of finding the l and r part, We can make that histogram and the answer for a query will be the largest rectangle in the subhistogram that contains the columns from a to b - 1, One of the ways to solve it is to try some heights h and see the maximum width we can achieve if h was the height, call it w, and maximize with h * w, To solve the slight difference in formulas problem we'll just maximize with h * (w + 1)!!
Let BU be a value the we'll choose later, We have 2 cases for our largest rectangle's height h, It could be either h ≤ BU or h > BU, We will solve both problems separately.
For h ≤ BU we can maintain BU segment trees, Segment tree number i has 1 at index x if lcpx ≥ i and 0 otherwise, When we query, It should get us the longest subsegment of ones in the query range, Let's see what we need for our merging operation, If we want the answer for the longest subsegment of ones in a range [l;r], Let mid = (l + r) / 2, Then the answer is the maximum between the answer of [l;mid], The answer of [mid + 1;r], And the maximum suffix of ones in the range [l;mid] added to the maximum prefix of ones in the range [mid + 1;r] . So we need to keep all these information in our node and also the length of the interval, As it's a well-known problem I won't get into more detail. Back to our problem, We can loop over all h ≤ BU, Let the answer for the query on range [a;b - 1] in segment tree number h be w, The maximum width of a rectangle of height h in this range is w and we'll maximize our answer with h * (w + 1) .
For h > BU, Let's call a column of height greater than BU big, The heights we'll try are the heights of the big columns in the range, We don't have to try all the heights greater the BU, There are at most 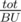 big columns (Where tot is the total length of strings in input), Let's keep them in a set, When an update happens, You should add the column to the set or remove it depending on its new height, The set's size can't exceed
big columns (Where tot is the total length of strings in input), Let's keep them in a set, When an update happens, You should add the column to the set or remove it depending on its new height, The set's size can't exceed 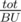 now, Let's see how to answer a query, Let's loop over the big columns in range [a;b - 1] only, If 2 of them aren't consecutive then the column after the first can't be big and the column before the second either, That's because if it were big, It would be in our set, So we can use this observation by making a new histogram with the big columns in the range only, And put a column with height 0 between any non-consecutive two, And get the largest rectangle in this histogram by the stack way for example in
now, Let's see how to answer a query, Let's loop over the big columns in range [a;b - 1] only, If 2 of them aren't consecutive then the column after the first can't be big and the column before the second either, That's because if it were big, It would be in our set, So we can use this observation by making a new histogram with the big columns in the range only, And put a column with height 0 between any non-consecutive two, And get the largest rectangle in this histogram by the stack way for example in 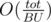 , The stack way will get us the maximum width w we can achieve for a rectangle containing column number i, We'll maximize with lcpi * (w + 1).
, The stack way will get us the maximum width w we can achieve for a rectangle containing column number i, We'll maximize with lcpi * (w + 1).
Also the answer for our main formula can be an interval of length one, All what I mentioned doesn't cover this, You should maintain another segment tree that gets the maximum length of a string in a range for this .
Maximize all what we got, You have the answer, Now it's time to choose BU, It's optimal in time to choose BU near 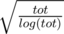 (Reason in tfg's comment below) .
(Reason in tfg's comment below) .
Optimization: The longest subsegment of ones problem is solved by BU segment trees and each one has 4 integers in each node, You can make them 2 integers (max prefix and suffix of ones) and make another only one segment tree that has the rest of the integers, That would divide the memory by 2 .
Time complexity : 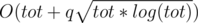
Thanks to vintage_Vlad_Makeev for making it harder and more interesting .
Solution link (vintage_Vlad_Makeev) : https://pastebin.com/vQ4RJqh0 .
Solution link (mahmoudbadawy) : https://pastebin.com/t3Vetzwf .










Auto comment: topic has been updated by mohammedehab2002 (previous revision, new revision, compare).
Light speed system test+Light speed editorial
Folks, now I can die in peace.
Give your RIP credit to light speed rating update too!!!
The editorial for F is wrong when it says the optimal choice of BU is sqrt(tot).
We want to minimize F(BU) = BU * log(tot) + tot / BU. Derivating this function and making it equal to 0 we have 0 = log(tot) — tot / BU^2, tot / BU^2 = log(tot), BU^2 = tot / log(tot), BU = sqrt(tot / log(tot)). So we want BU = sqrt(tot / log(tot)) and that is around 70~80.
Please correct me if I'm wrong.
Edit: to clarify, if we have BU = sqrt(tot) each query is O(sqrt(tot)*log(tot) + sqrt(tot)) = O(sqrt(tot)*log(tot)) and if BU = sqrt(tot / log(tot)) it is O(sqrt(tot * log(tot)) + sqrt(tot * log(tot))) = O(sqrt(tot * log(tot)) < O(sqrt(tot) * log(tot))
Yes, you are right.
You should take BU=sqrt(n/logn). I'll fix it now.
Thank you, I've edited it .
In c question why was pw chosen as 2^17?
It's just a large power of two less than 106 and greater than 105, Being a power of two makes our solution always correct and being greater than 105 makes it always distinct .
Could you please illustrate an issue that occurs if
pwis not a power of 2?Well, The correct condition isn't that pw should be a power of 2, The correct condition is that the value of the least significant bit with value 1 in pw should have a value greater than 105, The best and most straight forward way to find a suitable pw is being a power of 2, In fact choosing pw = 217 + 218 is OK. The least significant bit with value 1 is the first bit from the right that has the value 1.
Correct me if I wrong, but I believe that
pwcan be any number in[100000+1, 1000000/2]range if you use{pw, pw*2, pw^(pw*2)},{0, pw, pw^x^y}triples. You destroy allpwbits when XOR triplets. See this submission.How will the first solution for problem D work in less than 15 queries?
assume n = 1000, and the binary string is "111.....1110"
Every time you check the left half we find it full of ones, then we go check the right one, in a scenario like that we query for almost 20 times.
Did I miss something?
You'll check the first half and find it full of ones so you won't check the second, You'll check the first half of the second .
Check for [1;500], Full of ones, Check for [501;750] etc. , That way it's log(n)+1 queries at most not 2*log(n)+1 .
Thanks, got it.
mohammedehab2002
For problem C, I believe it should be n-2 instead of n-3, since you only add 2 more integers.
EDIT: My bad, I didn't notice that you add 0 as well.
In div2C i can't understand why i should stop on n-3 ? why not to choose any other number!
You can, This is just one of the solutions.
Also, you can check out my code.
n - 3 is the maximum number of elements we could print without having to change it later, For example : In Osama_Alkhodairy's solution, When he stopped at n - 1 he had to change it later, If you stop before n - 3, you'll have to print more numbers with your hand so n - 3 is a good choice .
Problem E, I don't get it. "- c not c because we are minimizing c + second not c - second" Why? :(
Because |c+second| = |second — (-c)|,so our goal is to minimize the difference between second and -c.
Oh, makes sense. Thank you.
The following is a solution for problem 862A - Mahmoud and Ehab and the MEX that does not require an array, and is not restricted to 100 elements at most with n <= 100.
30534732
Thanks for problem C and the editorial! :'). Couldn't solve it during the contest but have understood it now.
Also there were lots of comments that people have used randomized algorithms for C. Can anyone provide me an explanation or a link to the explanation? Thanks! :').
Also any suggestions on where to find tutorials for randomized algorithms?
I noticed that some solutions of F builds the segtree to query in one go, which has a < 1000ms runtime, however I am unable to understand. Would anyone mind explaining them?
Thanks in advance. =]
I can explain my solution (30552018). Not entirely sure if this is what you mean, but it is somewhat different from the solution in the editorial and (I think) an interesting alternative way to solve the problem.
First note that the stack in 'the stack way' (as mentioned in the editorial) can never get very large, at most about O(sqrt(tot)), assuming we keep the lcp-values on the stack distinct. Now for an interval in the segment tree, keep two stacks: one 'forward' and one 'backward'. Both of these stacks have at most O(sqrt(tot)) values. We can use the stacks and best value of two adjacent intervals to calculate the stacks and the best value for the combined interval. All this can be done in time linear in the stack sizes. Since we have O(lg(n)) levels in our segment tree, this gives an upper bound of O(sqrt(tot)*lg(n)) per query.
Thanks for the detailed explanation. =]
It seems that others who have a very short runtime are building the segtree same as yours, and it's surprising that the fastest one runs in 374ms (@dreamoon) despite of both solutions have the same asymptotic complexity. Not to mention that it takes way less memory. =O
Is it rated?
Yes, it was!
In the solution of problem E, the formula for LCP(str_1, str_2, ..., str_k) is wrong. It says minimum of LCP(str_i, str_i + 1) while it should be LCP(str_i, str_(i+1)).
Thanks, edited .
Hm. In problem F, It seems that the reason of adding string stuff is just to hidden constraint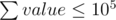 . It is easy to guess the solution if state it explicitly.
. It is easy to guess the solution if state it explicitly.
In div2 b problem , i have used bfs instead of dfs and it is giving wrong answer on testcase 9. Can anyone help me out in this problem pls.?
I have an alternate solution for PROBLEM C
Main idea: We use the fact that xor sum of $$$4k$$$, $$$4k+1$$$, $$$4k+2$$$ and $$$4k+3$$$ is $$$0$$$ for all non-negative integers $$$k$$$.
Then we handle cases when $$$n$$$ is congruent to $$$0$$$, $$$1$$$, $$$2$$$, $$$3$$$ $$$ mod $$$ $$$4$$$. So like if $$$n$$$ is congruent to $$$3$$$ $$$mod$$$ $$$4$$$, we have to use $$$3$$$ integers so that their bitwise XOR-sum is $$$x$$$ and the XOR of the rest of the numbers is 0, by the Main Idea above.
Link to my submission: 80259673
In problem D(interactive problem) how can I terminate with 0, if my code exceed the maximum number of queries?
You can maintain a global variable and before each query you can use
where $$$tot$$$ is your global variable and $$$15$$$ is the maximum number of queries allowed.