CODE FESTIVAL 2017 Qualification Round A will be held on Saturday (time). The writer is sugim48 and DEGwer.
This is one of the three qualification rounds of CODE FESTIVAL. In total, 20 foreign students will qualify in three rounds (Check the official site for detailed rules). If you are eligible for the onsite contest, please don't forget to fill the form at https://krs.bz/rhd-itm/m/codefes2017_en. Please check the detail of the tournament at http://codeforces.com/blog/entry/53502.
The contest duration is 2 hours, and there will be 6 problems. The first 4 problems are mainly used for choosing domestic students and much easier than other tournament competitions. However, we added two more problems and we hope these are interesting and challenging enough for choosing 20 qualifiers. Note that there is no time penalty for incorrect submissions. The time penalty is MAX, not SUM.
The point values are 100 — 200 — 400 — 700 — 1600 — 1600. If you are unfamiliar with AtCoder System, 2X-point problem in AtCoder is as hard as TopCoder's d1 X-point problem.
Let's discuss problems after the contest.











reminder(14 mins)
How to D? :D
Don't doublepost.
For odd d, you can color diagonals. For even d, this pattern works:
I'm lucky I got my internet connection to work 2 minutes before the contest ended...
When D is odd, do checkerboard pattern with just two colours.
When D is even, tile the plane using a diamond of size D - 1 × D.
Can someone give an explanation for Task F, Sample 4? How is it done in just 10 Operations?
After squeezing leftmost 3 and 4 using 2 moves each you are left with sequence 5 9 2 6 5 3 and 6 moves. Then you make
I hope the format is understandable
Excuse me, how is it possible to solve D in 2 minutes :|? It took me half an hour xd
It's enough to give a problemset on colorings to 7th grade pupils in a mathcamp once
I started with something like
using rather standard idea "let's split everything into blocks so that distance within one block is not large enough and distance between blocks is too large", and then it took me an hour to understand that all I need to make first distance smaller than second is to rotate everything by 45 degrees.
One reason: If d = 2k, then the points (0,k), (0,-k), (k,0), and (-k,0) are pairwise distance d from each other, so they should all be different colors.
I had this very early and still couldn't solve it for long time.
I have seen the solutions of this problem and many have done this
x = i+j
y = i-j
x = x%(2*d)
y = ((y%(2*d)) +(2*d) )%(2*d)
Why have they used 2*d and not just d?
You can use a trick which is similar to 763B - Тимофей и прямоугольники
The main idea is to combine two boards. The first board should have every two cells with |x+y|-|x'+y'|=d different in color. The second board should have every two cells with |x-y|-|x'-y'|=d different in color. Then you can combine the two boards with 2 different colors to one board with 4 different colors. The code is very simple.
my submission
How to solve F? The editorial is way too complicated, I couldn't understand =(
I thought about it in greedy way. I process groups from left to right and for every prefix I want to know the answer for prefix and for that best answer I also want to know greatest number of operations that can affect next slime (<=> operations that included last slime). One can see that these can easily be computed by some caseology and that it is not possible that if we allow ourselves one more operation on prefix then number of operations that we can use for suffix will grow by more than 1, what we need for correctness.
Let bi = ceil(log ai).
Notice that if b1 > b2 > ... > bn then answer is b1.
Think about greedy. Result may look smth like this.
May be somebody could explain the problem F more verbosely and formally?
I have looked in Japanese editorial, and it seems, that it somewhat different that english one.
I can explain my solution. You'd better try somewhere else, for example, several comments above, here is nice and short code, while my solution does nothing greedily and seems to be formally proved, but seems more complicated to me than others' solutions (however, I'll use sentences like "it's clear that ..." and "there is clearly no sense to ...", so the text below isn't completely formal).
First, consider the initial slimes. They can be divided into groups (i-th of them having ai consecutive slimes) so that no two slimes from different groups will never be combined. We watch the numbers of slimes in these groups, we start from (a1, ..., an) and end with (1, 1, ..., 1) (to clarify I remind that there are always n numbers).
Each operation consists of choosing a subsegment [l, r], dividing each ai with l < i < r by two (thus we require them to be even before this) and turning each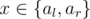 into an arbitrary number from
into an arbitrary number from 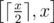 .
.
Next we notice that each operation doesn't change popcounts of internal elements of the corresponding subsegment. This means that each ai which is initially not a power of two should be the left-/rightmost element of a subsegment at least once.
Assume that all ai-s are powers of two. Consider (bi)i = 1n instead where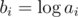 . Each operation now is decreasing by one on a subsegment. It's not hard to prove that the answer to the problem is
. Each operation now is decreasing by one on a subsegment. It's not hard to prove that the answer to the problem is
Indeed, one can imagine something like a Young tableau of b (except b isn't sorted) and then erase common edges of the i-th and the (i + 1)-st columns thus obtaining a division into horizontal rectangles representing the required subsegments.
Now let's see that each ai which is not a power of two has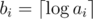 and the upper (if we imagine it with positive gravity) unit square of a Young tableau is cursed (that means, it should keep one of its edges present and not erased).
and the upper (if we imagine it with positive gravity) unit square of a Young tableau is cursed (that means, it should keep one of its edges present and not erased).
One can wonder why the uppermost unit square. Well, if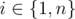 or if min(bi - 1, bi + 1) < bi then such an edge will exist anyway, for example, the uppermost one. Otherwise we add 1 to the answer anyway no matter which square is cursed, so let this be the uppermost.
or if min(bi - 1, bi + 1) < bi then such an edge will exist anyway, for example, the uppermost one. Otherwise we add 1 to the answer anyway no matter which square is cursed, so let this be the uppermost.
However, if two adjacent columns have the same height and each of them contains a cursed square then we can keep one edge for both of them and thus increase the answer by 1 instead of 2, so we should handle such partition of cursed columns into pairs.
Here is my code. One can see that actually there is no need to divide the initial array to 1-free regions manually,
get(a)should return the answer as well.