Rating changes for last rounds are temporarily rolled back. They will be returned soon. ×

wish_me's blog

Number of n-digits non-decreasing integers
By wish_me, history, 7 years ago, In English

Given an integer n > 0, which denotes the number of digits, the task to find total number of n-digit positive integers which are non-decreasing in nature.

A non-decreasing integer is a one in which all the digits from left to right are in non-decreasing form. ex: 1234, 1135, ..etc.

Note :Leading zeros also count in non-decreasing integers such as 0000, 0001, 0023, etc are also non-decreasing integers of 4-digits.

Examples:

Input : n = 1

Output : 10

Numbers are 0, 1, 2, ...9.

Input : n = 2

Output : 55

Input : n = 4

Output : 715

where n<10^3

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Good day to you,

Imho some DP could be used for this purposes. The parameters might be [DigitsRemaining <=10^3][LastUsedDigit <10]. In body, we could simply try all digits betweer <LastUsedDigit,9>.

We call such DP with [n][0].

If they want the output "by modulo" then it shall be easy like this with complexity A(N*10*10). In other case some efficient BigInteger structure shall be used (but It might also pass, since there won't be more than 10^(10^3) numbers :P)

Good Luck & Have Nice Day!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you explain more sir?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      What part exactly?

      It might look like following pseudocode: (+/-)

      dyn (remaining, last):
  Some end-of-recursion
  DP-check (if visited, end)
  for (i: last → 9) : dp[remaining][last]+=dyn(remaining-1,i)
  return dp[remaining][last]

      So some recursion on such base.

      GL

      → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +15 Vote: I do not like it

Let's observe that the final number will have some digits 0 (possibly zero), some digits 1 (possibly zero), some digits 2 (possibly zero), etc.. In total, there will be n digits and they must be in non-decreasing order. For any combination of digits, there will be only one number that satisfies the non-decreasing condition, so let's see the problem in this way: We have 10 boxes and we have to distribute n balls into them. This is a fairly known problem and the answer in this case is .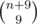

→ Reply