We are given 2 nodes s and t, and M queries that have one edge that needs to be deleted [only for this query], and for each query you need to output the shortest path between s and t. Note that s and t do not change.
1 ≤ Number of Nodes ≤ 7000
1 ≤ Number of edges ≤ 50000
1 ≤ Number of queries ≤ 10000
I couldn't find anything over the internet. I was thinking of something along the walks of pre-computation on a Dijkstra tree/Shortest path tree but couldn't think of anything. Can someone please provide hints or an approach to this problem?











Does deletion means turning weight to 0 and keeping the edge or complete removal of the edge?
I dont know how MaxFlow/Min Cut works. But this link may help you
https://stackoverflow.com/questions/10895259/shortest-path-in-absence-of-the-given-edge
I've seen that link, but there exists a much simpler solution not involving Max Flow/Min Cut I believe
The word "cut" does not mean that you need some mincut algorithm. Let's explain it in other words.
For a given edge e we can define two sets of edges: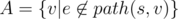 and
and 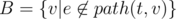 . path(x, y) is some shortest path between x and y. We will assume that
. path(x, y) is some shortest path between x and y. We will assume that 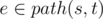 , otherwise the answer is obvious.
, otherwise the answer is obvious.
It's easy too see that each vertex lies either in A or in B. Consider the earliest moment when we go from the vertex in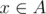 to the vertex in
to the vertex in 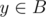 . By definition, we can go from s to x by the shortest path in the original graph, the same is true for y and t. So the path is uniquely determined by the edge xy. We just need to go through all edges xy such that
. By definition, we can go from s to x by the shortest path in the original graph, the same is true for y and t. So the path is uniquely determined by the edge xy. We just need to go through all edges xy such that 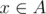 and
and 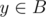 .
.
It works in O(qm) for queries and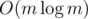 for shortest paths precomputations. Also there is a way to sped up it to
for shortest paths precomputations. Also there is a way to sped up it to 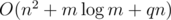 .
.
That makes sense, I understand your solution, thanks! But for each such edge xy, we have to iterate through all edges in our shortest path and update the answer for this edge in our pre-computation right?
Doesn't that make the complexity O(M*N) rather than O(MlogM)? [since there can be at most N edges in the shortest path]
No, for each edge xy we just use precomputed values of d(s, x) and d(y, t) in the original graph.
Couldn't the path d(s,x) -> edge xy -> d(y,t) be an answer for all edges in our shortest path d(s,t)?
So we're iterating through all such edges xy and updating the answer for all edges in our shortest path during pre-computation, right?
No, in precomputation we only build two Dijkstra trees, from s and from t. We need them to find sets A and B.
For each query we find A and B, iterate through edges, and find the answer.
Isn't this the Facebook problem from ioitc 2012?!
Yup, it is the same problem and same constraints.
Since answer for edges not on original shortest path is the same, ignore those.
Consider the dijkstra/shortest path tree of the graph from s. In this, if you delete an edge on the shortest path to t, the tree splits into 2 parts, if you can appropriately find the "bridge" between these 2 components, you can solve the problem.
For finding that, consider an edge (u, v, d) not in the original dijkstra tree. Assume in the dijkstra tree , The shortest path going via this edge has weight D(s, u) + D(v, t) + d where D(a, b) = distance b/w nodes.
in the dijkstra tree , The shortest path going via this edge has weight D(s, u) + D(v, t) + d where D(a, b) = distance b/w nodes.
So this edge may form the shortest path bridge when we disconnect some other edge on path(u, v) in the tree. This reduces the problem to path update + edge query, which can be handled offline(or with HLD).
Time complexity: O((N + M)·log(N + M) + Q)
Thanks! But how do you handle offline processing efficiently? I can't think better than O(M*N)
You can just use straightforward HLD.
Or, since you only need to worry about edges on path s -> t, this is equivalent to saying you have an array of edges b/w s to t sequentially(each having value infinity) and some range updates (L, R, w) which describe “set the value of all elements between (L,R) to min(current value, w)”, this can be done using set or something and iterating from left to right, activating and deactivating the updates.