A straightforward implementation problem. Calculate the total distance and then the average time.
For each integer i, we denote its total number as a[i]. Note that only a[i] / 2 (integer division) of them can be used to construct a frame. Thus, the total number of frames that can be built is 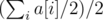 .
.
This is also an implementation problem, but we should take care of the following issues:
1) several special cases like t0 = t1 should not be omitted;
2) to find the pair (y1, y2) so that the temperature is closet to t0, it is better to use “integer computation” rather than “double computation”, since the latter one may meet some weird “precision trap”.
The problem can be solved based on the well known KMP algorithm. Specifically, we use the array next[i] in KMP (one can find a lot of details about this on the Internet).
At first, we check next[n]. If it is zero, it means that the answer is definitely “just a legend”; otherwise, we check all next[i] with i = 2, 3, ...n - 1. If at least one of them is equal to next[n], we just find the answer. If there is no such index, we should further check next[next[n]]. If it is zero, it implies that the answer is still “just a legend”, which can be proved by contradiction; otherwise, we just find the answer again.
It turns out that the problem is not that difficult if we have noticed the following rules.
We first focus on the right upper corner point, (1, n). It can be seen that this point only depends on whether there is a command (1, n). Thus, by observing this point, we can determine this command. Then, we move to point (1, n - 1), and it depends on both the commands at point (1, n) and (1, n - 1). As we have known the command of point (1, n), we can immediately determine the result of (1, n - 1) as well. Similarly, we move to point (1, n - 2) and use the above arguments again.
In general, we enumerate rows from 1 to n, and for the i-th row, we enumerate columns from n to i + 1. After this, we have determined the command at all the points (i, j) with i < j. Then, we enumerate rows from n to 1, and for each row we enumerate columns from 1 to i - 1. After this, we have determined the command at all the points (i, j) with i > j. Finally, we enumerate points (i, i) from i = 1 to i = n and determine the command at points (i, i).
Although n is up to 1018, in fact it is sufficient to consider the first 100 Fibonacci integers, since it increases at the order of about 2i.
We write the Fibonacci sequence as f[i] = (1, 2, 3, 5, ...) also adopt an array a[i] which is initialized with zero. For the given integer n, we find the maximum Fibonacci integer that is not larger than n as f[j] and then set a[j] = 1. Next, we set n to n - f1 and repeat this process until n is reduced to zero. For instance, if n = 13, we have a[i] = (00000100...), while for n = 7, we have a[i] = (0101000...).
Then, let us consider a[i]. For (00001), we can change it into (00110) and further into (11010). Thus, we adopt another array h[i], which denotes the number of consecutive zeros to the left of index i. For instance (00001001), we have h[5] = 4, h[8] = 2 while the other values are zero (indices start from 1).
Finally, we use dp[i][0] to denote the total number of decomposition under the condition that the i-th 1 in array a[i] is changed into zero; while use dp[i][1] to denote the total number of decomposition under the condition that the i-th 1 is not changed into zero. The recursive formula is dp[i][0] = dp[i - 1][0] * ((h[i] + 1) / 2) + dp[i - 1][1] * (h[i] / 2) and dp[i][1] = dp[i - 1][0] + dp[i - 1][1].









