You are given a set S of n strings. Sum of length of all the strings <= 2 * 10^5. Now you have to find the size of the smallest generating set for these n strings. The smallest generating set is the minimal subset of the set S such that by concatenating some of its strings multiple times you can generate all the strings in the set S.
For example let the set S contains strings "ab" , "abb" , "b" and "a" then the answer is 2 as you can have a set {"a" , "b"} which is the subset of set S and using these strings you can generate all the 4 strings. Also you can concatenate any string >= 0 times.
Link to the problem statement.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/27/2024 05:26:47 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











In the problem itself it's stated that you need to pick some subset from the given set you have. this makes your example invalid since you included "e" in the generating set, right?
Sorry that was a major mistake. Thank you for pointing it out. But still I don't have any solution to the problem.
Auto comment: topic has been updated by Apptica (previous revision, new revision, compare).
Sort the strings by their length. Then you should add to your subset string number i only if it cannot be created by concatenating some strings with smaller length. Well now the problem simply becomes finding whenever a string can be decomposed into strings such that every string appears in your initial set. This can be done with hashing in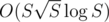 , where S is the sum of lengths. The main observation to achieve such a complexity is that there are at most
, where S is the sum of lengths. The main observation to achieve such a complexity is that there are at most 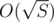 different lengths of the strings in the dictionary.
different lengths of the strings in the dictionary.
It can be further optimized with suffix automaton or Aho Corasick to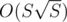 .
.
Please can you elaborate a bit on how to check if there is any decomposition possible. I am thinking something related to suffix but that over runs the complexity.
We will have dppos equal to 1 if we can decompose the prefix untill pos and 0 overwise. Obviously then to check if a string can be decomposed we are interested in only dplen where lwn is the length of the current string.
You can compute all dpi easily in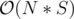 with hashing — for every position you go through all words and check if they match on the ending position and if this is the case you can se if decomposing the prefix untill position i - L where L is the current "pattern" string's length.
with hashing — for every position you go through all words and check if they match on the ending position and if this is the case you can se if decomposing the prefix untill position i - L where L is the current "pattern" string's length.
Now to achieve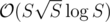 time complexity you will have to use the observation that there are at most
time complexity you will have to use the observation that there are at most 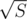 different lengths of the words — it can be easily proved.
different lengths of the words — it can be easily proved.
Well we will use the previous DP but instead of trying all strings for every position, we will try all lengths and then check if the hash of that suffix of the current prefix appears in the initial words. This can be done with a std::map which stores all hashes that appear in the initial words.