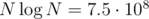Given an integer N, find how many pairs (A, B) are there such that: gcd(A, B) = A xor B where 1 ≤ B ≤ A ≤ N. Here gcd(A, B) means the greatest common divisor of the numbers A and B. And A xor B is the value of the bitwise xor operation on the binary representation of A and B. Input The first line of the input contains an integer T (T ≤ 10000) denoting the number of test cases. The following T lines contain an integer N (1 ≤ N ≤ 30000000). Output For each test case, print the case number first in the format, ‘Case X:’ (here, X is the serial of the input) followed by a space and then the answer for that case. There is no new-line between cases. Explanation Sample 1: For N = 7, there are four valid pairs: (3, 2), (5, 4), (6, 4) and (7, 6).
Sample Input
2
7
20000000
Sample Output
Case 1: 4
Case 2: 34866117
Link:https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4454
i am not getting any idea, how to solve this problem. Thanks in Advance :)










I have a solution in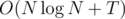 time and O(N) space. It should TLE because N is very high but I feel like I'm not far from the actual solution and maybe someone could continue me:
time and O(N) space. It should TLE because N is very high but I feel like I'm not far from the actual solution and maybe someone could continue me:
First, we can observe that, gcd(A, B) ≤ A - B, and AxorB ≥ A - B. Therefore, the pairs (A, B) must satisfy gcd(A, B) = AxorB = A - B.
For a gcd value g, the form of pairs that their gcd is equal to their difference, and is equal to g, are of the form (g * (X + 1), g * X). For the xor I've yet to find some generalization.
Here's what you can do: Create a table T[N] initialized to 0. for each pair (A,B) we find, we will increment T[A] by 1. Here's how we find those pairs:
For every gcd g from 1 to N, go over all pairs of the form (g * (X + 1), g * X) (There will be N / g of them). If the current pair has a xor equal to g, increment T[g * (X + 1)] by 1.
The amount of pairs you will go through is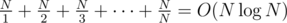 .
.
After this, maintain the partial sum of the array T: (the following is with 1-indexing)
Then you can answer each query in O(1) by just outputing T[z] where z is the value given in the query.
Correct me if I'm wrong somewhere.
Edit: Actually there's a time limit of 5 seconds, and the preprocessing doesn't have a high constant, so it might fit in the time limit.
Here's a short c++ implementation of the above solution:
Noam527
First, we can observe that, gcd(A, B) ≤ A - B, and AxorB ≥ A - B. Therefore, the pairs (A, B) must satisfy gcd(A, B) = AxorB = A - B.
Hmmm, is there a theory behind this part? or did you just observe and notice this one? Curious x) .
For the gcd part: suppose gcd(A, B) = g. If we divide both by g, their difference will be divided by g as well (and still be an integer). So how can their gcd by higher than their difference? Well something I just noticed (an edge case I didn't mention but doesn't matter) is if A = B. But in this case, gcd(A, B) = A, and A xor B = 0, so there are no such pairs.
For the xor part: suppose we want A xor B to be smaller than A — B, or in other words, minimal. Xor inverts bits, so in order to make the xor operation subtract as much as it can from A, all B's set bits must be also set in A. This makes their xor A — B and this is the minimal achievable.
Nice explanation. Never thought of that xor property before.
A more rigorous way to prove these claims:
It's fairly straightforward that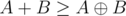 . Then
. Then 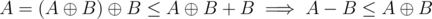
Your solution could be improved by using the fact that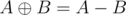 iff
iff 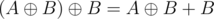 . Since
. Since 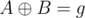 , then
, then 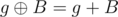 . This is satisfied when g&B = 0 or g&(X·g) = 0. After some investigation it seems that the solutions to this equations are periodic with a period of at most
. This is satisfied when g&B = 0 or g&(X·g) = 0. After some investigation it seems that the solutions to this equations are periodic with a period of at most 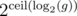 . This means that the total number of operations is
. This means that the total number of operations is 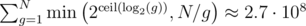 . This is quite borderline but still an improvement from
. This is quite borderline but still an improvement from