Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | jiangly | 3578 |
| 4 | orzdevinwang | 3570 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | tourist | 3565 |
| 8 | maroonrk | 3531 |
| 9 | Radewoosh | 3521 |
| 10 | Um_nik | 3482 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
| Name |
|---|



How do you find ?
?
For those who upvoted my question above :)
Say, a sequence of numbers sum to t. Out of all such sequences, what can be the gcd of all numbers in the sequence? It has to be a divisor of t. Let it be d = gcd(a1, ..., ak). Because all ai is divisible by d, thus the sum is also divisible by d, where the sum is t.
Hope this helps..
in the formula we can g value directly, but f value need other f value.
but the accepted code seems like calculating f(t) with this:f(t)=2^(t-1)-sigma(2,ti)[g(t/ti)].
such as the #1 and #2 on the standing list
can u explain that......?
Say t has divisors 1 = t1 < t2 < ... < tk = t. Then the formula for g will be as follows: . Here the first component of the sum is the actually f(t) itself, as t1 = 1
. Here the first component of the sum is the actually f(t) itself, as t1 = 1 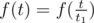 . Hence, we get
. Hence, we get 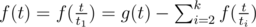 .
.
ai mustn't divide t, for example 2 + 3 = 5 but 2 doesn't divide 5 All what matters is that sum(ai)=t => d*sum(ai/d) = t => there is a k so that d * k = t => d|t
where do I say that ai divides t?
Oh my fault sorry. I think I had misread your answer
No need for set in problem C. You should only keep largest element and second largest element. If we are currently at Ai, and if largest element before Ai is > Ai, second largest is < Ai, then that element can become record by removing largest element, so increase cnt[ A_largest_before_i ]. array cnt tells the change when we remove that element. It is important to set cnt[ Ai ] to -1 before algorithm if Ai is initial record, and later it may be increased. We set it to -1 because removing it surely removes one record, and later we will increase it if it also "creates" other records.
Hi I had thought of something like this but have a doubt.
Can you please answer the query over here in this comment?
Thanks!
Oh, your solution sounds exactly like one found by me! I've solved the problem in C language, but after the contest has already ended... (((
what will be output for following test case? and how ? please reply 5 elements : 4 3 5 1 2
See my second submission to this problem for a solution following this format. We first get r[] = {1,0,1,0,0} and initialize x[i] = {-1,0,-1,0,0}. We loop through a[] and keep track of max and max2, indices for the 1st and 2nd largest term so far. We know that if a[max]>a[i]>a[max2], that's another "contribution" for max so x[max]++.
The only x[max]++ here happens at i = 1, x[0]++. After the loop, you get x[i] = {0, 0, -1, 0, 0}, so we find the smallest a[i] with x[i] = 0 -> 1.
hello,i saw your code and ran it for the test case 5 1 2 3 5 4 it gave the answer 5 while even if we remove 4 the number of records is going to be the same.Can you please explain where am i mistaken?
I found g(t) = 2t - 1 in a different way. Can you elaborate a bit more on this: represent all integers in the sequence in unary system with zeros, and split them with t - 1 ones.
It's a bug. Correct explanation should be: decrease by one all integers in the sequence, represent them in unary system with zeros, and split them with ones.
How does this give the answer (2t - 1) directly(!)? a bit more clarification..
I summed up the number of solutions to the equations like: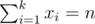 , which has Cn - 1k - 1 number of solutions. Then the answer is
, which has Cn - 1k - 1 number of solutions. Then the answer is  .
.
It was an attempt to construct a bijection between the bit representation and the sequence. Imagine, that you are reading bit representation and constructing suitable sequence. If you meet 0, you should add 1 to the previous member of the sequence, else you should add 1 to the previous member and start next member with 1.
You can think of it like this way. We have n ones in a lines. Let's say our n = 5. This will correspond to 11111. Now, there are are 4 positions in between those "ones" (more precisely, consecutive ones) where we can place a barrier. What I mean by barrier is like this (11|11|1) where | represents a barrier, hence our paritition will be (2, 2, 1) for 5 or we can place our barriers like this (1|111|1) where our partition will be (1, 3, 1) or like this (111|1|1) which corresponds to another valid partition (3, 1, 1). Hence, we can say that at each of 4 positions, we can choose to place a barrier on it or not and it will always produce a unique partition. Therefore, we have 2(5 - 1) = 24 choices (2 because we can have a barrier in between consecutive ones or not). Hence, if we have n ones, we'll have n - 1 barriers to place, so we'll have 2n - 1 choices to make. Interstingly, this technique can be used to prove some more important problems, like proving "dividing n among k groups where each group gets atleast 1 which we can say selecting by k - 1 barriers out of n - 1 barriers". I hope you understand it now.
Beautiful!!
My solution above actually uses this technique, but for a fixed k, therefore I was summing up for all possible values of k. I was just wondering how to find it at one step! And your clarification made it very easy, thanks!
Thank you for your nice explanation. But I can't figure out a situation. The editorial states that "Let's denote the number of sequences such that their sum is t as g(t). Then g(t) is 2^(t - 1): represent all integers in the sequence in unary system with zeros, and split them with t - 1 ones".
But let t=3. Then g(3)=2^(3-1) = 2^2 = 4. But we can make 3 sequence whose sum is equals 3. they are-
1+1+1=3 and 2+1=3 and 3=3
Then how g(3)=4 ? Please help me to figure out this situation. Thanks in advance.
1 + 2 = 3
Hello, thank you for the contest!
I think in problem D there were some submissions that shouldn't pass but before of the tests they did. At least this one: http://codeforces.com/contest/900/submission/33138278 The case x=1, y=999999527 (which is prime), it lasts like 15 seconds.
I am not asking to reevaluate of course, just bringing it to your attention.
Thanks again for the contest
Thank you, we didn't think about such case. We'll be more attentive next time.
What is the maximum answer for C? I iterated only 1000 times. That was enough. But i'm curious, is my approach correct? I know that period's length can be at most b — 1.
I didn't understand D. Can someone please explain it in more detail. Especially, the part on, how we calculate the value of g(t). Also, how f(t) is obtained from g(t) then.
That's how I understand it.
First if x does not divide y, then the answer is zero, since the gcd has to divide every number, it must divide the sum.
Now to the case where x divides y, we need to calculate all sequences that sum to y / x with gcd 1, why? Because any valid sequence can be transformed to such form if you take the gcd as a common factor. Let's say a1 + a2 + a3 ...an = y, and the gcd of a1,a2,a3.. an is g, then we can write it as g*b1 + g*b2 + g*b3...g*bn = y, which is the same as g*(b1+b2 + b3 +..bn) = y, now divide by g, and you get b1 +b2 +b3 + b4...bn = y/g.
Now to count the sequences of sum X and gcd 1, you start by saying that all sequences are valid, so you add all sequences that sum to X ( To get that number, check the comment by I_Love_Equinox, he explains it perfectly, or google stars and bars theorm).
After you do so, you need to subtract bad sequences with gcd > 1 and sum equal to y / x, the gcd must divide the sum again (y/x) , so you re-enumerate the process by finding numbers that sum to (y/x)/g, where g divides y /x. You keep doing so recursively.
Thank you. I get it now.
it's much more understandable right now, thanks
Maybe I am little shame now, but can someone explane me proof for size of period in the second task and explanation how it is connected with pigeonhole principle ?
Think it like this way. How do we actually calculate where a < b. We multiply a = a * 10 until a ≥ b, then in quotient of the division,
where a < b. We multiply a = a * 10 until a ≥ b, then in quotient of the division,  is appended and we calculate the new division for a%b. For example,
is appended and we calculate the new division for a%b. For example,  . We do a = 5 * 10 = 50. We append
. We do a = 5 * 10 = 50. We append 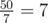 to our quotient and calculate 50 - 49 = 1. This 50 - 49 is nothing but 50%7 = 1 and hence we'll now start off the new step of the division from here (i.e. again multiply 1 with 10 and our new quotient will be 0.71...). So, if two remainders in the process are same, the whole process will repeat, and consequently the period will repeat. Since, there are b distinct remainders and
to our quotient and calculate 50 - 49 = 1. This 50 - 49 is nothing but 50%7 = 1 and hence we'll now start off the new step of the division from here (i.e. again multiply 1 with 10 and our new quotient will be 0.71...). So, if two remainders in the process are same, the whole process will repeat, and consequently the period will repeat. Since, there are b distinct remainders and  will always be ≤ 9, hence, due to pigeon hole principle, atleast one value of remainder will repeat and period will be
will always be ≤ 9, hence, due to pigeon hole principle, atleast one value of remainder will repeat and period will be 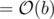
Thank you very much, I got it.
This proof for me looks harder than B div 2, but I would guess solution on the contest, possible as 70% of coders :P
Sorry for the naive question, but is the b in the O(b) equal to the b in the input?
Yes
Thank you so much.....i just took some really big number and got accepted but didn't knew the about this.
for D : A000740 , mu
How to solve E?
First of all, we need find if is possible make a string t starting of position i.
Lets make a dp only for odd positions. This dp[position][letter] answer the longest string can be create, just looking odd positions, starting with the letter in second state and only using this letter or '?'. Do the same thing for even positions.
There are in string t exactly ceil(|t| / 2) a's and floor(|t| / 2) b's (|t| is the length of string). So, to check if string t exists starting of position i, you can just look the previous dp check dp[i]['a'] >= ceil(|t| / 2) and dp[i]['b'] >= floor(|t| / 2)
The cost of make this string is exatly the number of '?' between indexes i and i + |t| — 1.
Now, we know if is possible to make string t starting to index i and which is the cost to do that. So, we can write another dp to solve the final part of the exercise.
If is possible make a string t starting on position i
dp[i + |t|] = best(dp[0 .. i]) + costStartingPosition(i);
In this case, dp[x] is a pair (maximum number of words, minimum cost).
So, the cost of make a string finishing on position i + |t| is the best cost between indexes [0 .. i] plus the cost of starting a word on position i.
This best(dp[0 .. i]) can be implemented with a segtree dp or just mantain the best dp of the indexes [0 .. i] in linear time.
Solution: http://codeforces.com/contest/900/submission/33138394
Does this question belong to a certain class of dp questions? If yes, can you suggest similar problems.
When I was solving this problem, the first "class of dp" that came in my mind was dp with segtree (because in this problem we need find the best of a range).
The only problem that I remember now about that is this http://codeforces.com/gym/100733/problem/F
If I remember another problems, I update this post :)
What are they discussing here ?
Announcement Section Discussion
As mentioned already in some comments in the discussion, fft could be used for general strings t.
For this one I did the following. First for each position pos find the maximum prefix of the word t that can be built, which ends in pos and count the cost of building it.
There are few cases: if pos has '?', you can extend the previous prefix if the previous prefix had length < m. If not you can either construct the prefix of length m (if you had at least m-1 continuos positions with '?' before pos) or m-1 (if there is at least one letter, it uniquely determines the prefix).
If pos has a letter you can try to extend it, if the parity of the previous prefix is ok (even for 'a', odd for 'b'). Again you will be able to extend it, if the length was < m, if not, you will be able to get m-1.
Whenever you add '?' or move the beginning and get rid of initial '?' update cost correctly.
The last case is when you can't extend previous prefix, which means that you have a letter at pos. In that case try to get as many continuous '?' as possible, ending at pos — 1 and create new prefix.
Once you computed the values above you just need to run simple dp to count maximum number of disjoint occurences and minimum cost of it.
Code for reference.
Thus we need for compute only f(ti) for every ti|t.What does this mean?
I think the B problem had weak test cases. I just found the first 1000 digits of the quotient and checked whether the digit was there or not. I got AC :)
I think I have a kind of cute solution for B — I just performed the division until the point I know the digits will repeat. My solution can be found here
A similar algorithm was used using C++ STL sets to find the position of the digit
cin problem 900B - Position in Fraction in the decimal (base-10) representation of the fractiona/bduring the contest, where items of the set are distinct co-prime pairs<a,b>,1 <= a < b <= N, whereN = 100000generated using long division of co-prime pairs computed using the__gcdfunction. This could lead to faster execution time whenbis non-prime.33128670
The aforementioned algorithm was extended as follows using C++ STL bitset and template for more efficiency, and to be used for any
Radixand anyNrather than 10 and 100000, respectively.33151934
Wasn't E significantly easier than D, or it's just me? I would give E the same difficulty as C.
+1
I would say it is more difficult since D is the only problem I need one submission to get accepted, but I could not solve E.
Yup. E is a trivial dp problem.
Can anyone explain how to solve D using Mobius Function ?
You should use Mobius inversion formula to solve D. At first we have such expression: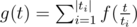 . If we use Mobius inversion formula, we are getting a new expression to calculate f(t):
. If we use Mobius inversion formula, we are getting a new expression to calculate f(t): 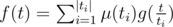 . Sorry for my bad English.
. Sorry for my bad English.
can you explain it with an example?
Sorry, what exactly do you want me to explain? Mobius inversion formula in general or its application for solving this problem?
Mobius inversion application to solve this problem.
Well, Snezhok in his editorial said that if y is divisible by x then the answer is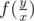 . He also said that g(t) = 2t - 1 and
. He also said that g(t) = 2t - 1 and 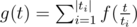 , where ti are divisors of t. So we know how to calculate g(t) (for example using binpow), but we need to calculate f(t). Using Mobius inversion formula, we are getting a new expression:
, where ti are divisors of t. So we know how to calculate g(t) (for example using binpow), but we need to calculate f(t). Using Mobius inversion formula, we are getting a new expression:  . Ok, now we can calculate
. Ok, now we can calculate 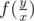 . How to calculate μ(ti)? This solution is enough fast so I didn't think about it too much. To calculate μ(ti) we need know its prime divisors. But each divisor of ti is a divisor of t too. So we can precalc prime divisors of t and use them to calculate μ(ti). Sorry for my English :)
. How to calculate μ(ti)? This solution is enough fast so I didn't think about it too much. To calculate μ(ti) we need know its prime divisors. But each divisor of ti is a divisor of t too. So we can precalc prime divisors of t and use them to calculate μ(ti). Sorry for my English :)
Auto comment: topic has been updated by Snezhok (previous revision, new revision, compare).
For Problem E,if both string S and string T is given and the length of them is between 1 and 10^5.Does there exist a solution that works in O(length) time or O(length log length) time?
Editorial solution has O(n) time complexity where n is length of s.
But if string t has an arbitrary form it is possible to use FFT algorithm to find positions where occurences can start. So time comlexity will be O(length log length) due to FFT.
"We know that the number of divisors of t is not greater than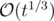 ". How do you prove this ?
". How do you prove this ?
e-maxx in his post said that he had found such an interesting fact here: "for all ε > 0, d(n) = o(nε)". He also gave other estimates but he said that on practice we use numbers less than 1018 so it's easier to use an estimate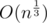 that is more rough than others.
that is more rough than others.
How to solve C — Remove Extra One if all elements are not distinct, that is the permutation of n integers p1, p2, ..., p_n (1 ≤ pi ≤ n) contains some repeated integers?
Thanks.
Permutation can't contain repeated integers by its definition. A permutation is a rearrangement of the elements of an ordered list S into a one-to-one correspondence with S itself. You can read about it here for example.
Ok,consider sequence but not a permutation.
For each 1 ≤ i ≤ n we can calculate how many records will there be in sequence if we remove a[i]. We can use
std::setorstd::mapfor it. If I'm not mistaken, this solution is right.Thanks...Just we need to keep the count of how many times you have seen it before which can be done using std::map or std::multiset... I was thinking to reduce further because it doesn't matter if we remove the next occurrence of an element
.
Not Able to understand C Editorial Help
The problem states that it would provide you a permutation of 1 to n Find out a single integer 'x' from the given permutation; which has the longest increasing subsequence to its right so that every number on that increasing subsequence is greater than all the numbers left to 'x' and every number on that increasing subsequence is strictly less than 'x'. If there are more than 1 such numbers with equal length of increasing subsequence at its right, pick the minimum one.
This is how I understood the problem and solved it.
Very bad editorial for novice programmers like me. 900B is not explained at all. How is it to be done? No code, no algorithm, nothing mentioned. Just Wikipedia links.
Please write editorials which can be useful for 'Pupils'